A. 推箱子
题目描述:
推箱子是一个很经典的游戏.今天我们来玩一个简单版本.在一个 \(M \times N\) 的房间里有一个箱子和一个搬运工,搬运工的工作就是把箱子推到指定的位置,注意,搬运工只能推箱子而不能拉箱子,因此如果箱子被推到一个角上(如图 \(2\) )那么箱子就不能再被移动了,如果箱子被推到一面墙上,那么箱子只能沿着墙移动.
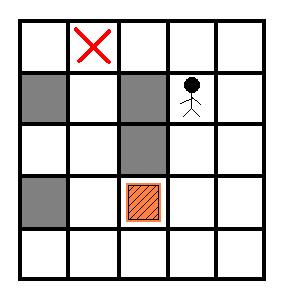
现在给定房间的结构,箱子的位置,搬运工的位置和箱子要被推去的位置,请你计算出搬运工至少要推动箱子多少格.
输入格式:
输入数据的第一行是一个整数 \(T\)(\(1 \le T \le 20\)),代表测试数据的数量.然后是 \(T\) 组测试数据,每组测试数据的第一行是两个正整数 \(M\),\(N\)(\(2 \le M,N \le 7\)),代表房间的大小,然后是一个 \(M\) 行 \(N\) 列的矩阵,代表房间的布局,其中 \(0\) 代表空的地板, \(1\) 代表墙, \(2\) 代表箱子的起始位置, \(3\) 代表箱子要被推去的位置,\(4\) 代表搬运工的起始位置.
输出格式:
对于每组测试数据,输出搬运工最少需要推动箱子多少格才能帮箱子推到指定位置,如果不能推到指定位置则输出 \(-1\).
样例输入:
1
5 5
0 3 0 0 0
1 0 1 4 0
0 0 1 0 0
1 0 2 0 0
0 0 0 0 0
样例输出:
4
数据规模:
见题面描述。
点击查看代码
int t;
int ax,ay,bx,by,cx,cy,n,m,step;
int f[10][10][10][10],a[10][10];
int dx[]={-1,0,1,0};
int dy[]={0,1,0,-1};
void dfs(int ax, int ay, int bx, int by, int cx, int cy,int step,int n,int m) {
if(f[ax][ay][bx][by] <= step) return;
f[ax][ay][bx][by] = step;
if (ax == cx && ay == cy) return;
for (int i = 0; i < 4; i++) {
int nx = bx + dx[i], ny = by + dy[i];
if(!(nx >= 1 && nx <= n && ny >= 1 && ny <= m && a[nx][ny] != 1)) continue;
if(nx == ax && ny == ay){
int tx = ax+dx[i],ty = ay+dy[i];
if(!(tx >= 1 && tx <= n && ty >= 1 && ty <= m && a[tx][ty] != 1)) continue;
dfs(tx,ty,nx,ny,cx,cy,step+1,n,m);
}
else {
dfs(ax,ay,nx,ny,cx,cy,step,n,m);
}
}
}
int main() {
scanf("%d", &t);
while (t--) {
scanf("%d %d", &n, &m);
memset(f,0x3f,sizeof(f));
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
scanf("%d", &a[i][j]);
if (a[i][j] == 2)ax = i, ay = j;//箱子
if (a[i][j] == 4)bx = i, by = j;//人
if (a[i][j] == 3)cx = i, cy = j;//目标位置
}
}
dfs(ax, ay, bx, by, cx, cy, 0, n, m);
int ans = f[0][0][0][0];
for(int i=0;i<4;i++){
int nx = cx+dx[i],ny=cy+dy[i];
if(1<=nx&&nx<=n&&1<=ny&&ny<=m&&a[nx][ny]!=1)
ans = min(ans,f[cx][cy][nx][ny]);
}
if(ans == f[0][0][0][0])cout<<"-1\n";
else cout<<ans<<endl;
}
return 0;
}
编译结果
compiled successfully
time: 2ms, memory: 392kb, score: 100, status: Accepted
> test 1: time: 0ms, memory: 392kb, points: 10, status: Accepted
> test 2: time: 0ms, memory: 392kb, points: 10, status: Accepted
> test 3: time: 0ms, memory: 392kb, points: 10, status: Accepted
> test 4: time: 0ms, memory: 392kb, points: 10, status: Accepted
> test 5: time: 0ms, memory: 392kb, points: 10, status: Accepted
> test 6: time: 0ms, memory: 392kb, points: 10, status: Accepted
> test 7: time: 1ms, memory: 392kb, points: 10, status: Accepted
> test 8: time: 0ms, memory: 392kb, points: 10, status: Accepted
> test 9: time: 1ms, memory: 392kb, points: 10, status: Accepted
> test 10: time: 0ms, memory: 392kb, points: 10, status: Accepted
B. 迷宫难题
题目描述:
这是一个 \(n\) 行 \(m\) 列的迷宫,某些格子有若干枚钥匙。相邻格子之间有一扇门,门上有若干把锁,所有的锁都打开才能够通行,若没有锁则直接通行。对应的钥匙可以打开对应的锁,钥匙和锁的类型范围由数字 \(0\) 到 \(p\) 表示。每一步可以走到周围四连通的格子之一,门可以从两个方向打开,捡钥匙和开锁不消耗时间。问从 (\(1, 1\)) 到 (\(n, m\)) 最少需要走多少步。
输入格式:
第一行三个整数 \(n,m,p\)。
第二行一个整数 \(K\),
接下来 \(K\) 行每行 \(5\) 个整数 \(x_1, y_1, x_2, y_2, t\),表示 (\(x_1, y_1\)) 与 (\(x_2, y_2\)) 之间的门上有一把 \(t\) 类型的锁。
保证 (\(x_1, y_1\)) 与 (\(x_2, y_2\)) 相邻。
下一行一个整数 \(S\),表示钥匙的个数。
接下来 \(S\) 行每行三个整数 \(x, y, t\),表示 \(x,y\) 处有一枚 \(t\) 类型的钥匙。
输出格式:
输出一行表示答案。
样例输入:
4 4 9
9
1 2 1 3 2
1 2 2 2 0
2 1 2 2 0
2 1 3 1 0
2 3 3 3 0
2 4 3 4 1
3 2 3 3 0
3 3 4 3 0
4 3 4 4 0
2
2 1 2
4 2 1
样例输出:
14
数据规模:
\(N,M,P \le 10\), \(K < 150\), \(S \le 150\)。
点击查看代码
#define MAXN 12
queue<pair<pair<int, int>, int> > q;
int n, m, p, k, x1, x2, y3, y2, t, s, x, y, cur, ans;
bool vis[MAXN][MAXN][2050];
int gate[MAXN][MAXN][MAXN][MAXN], key[MAXN][MAXN], dis[MAXN][MAXN][2050];
int dx[] = { -1,0,1,0 };
int dy[] = { 0,1,0,-1 };
int main() {
pair<pair<int, int>, int> cur;
scanf("%d %d %d", &n, &m, &p);
scanf("%d", &k);
for (int i = 1; i <= k; i++) {
scanf("%d %d %d %d %d", &x1, &y3, &x2, &y2, &t);
gate[x1][y3][x2][y2] |= (1 << t);
gate[x2][y2][x1][y3] |= (1 << t);
}
scanf("%d", &s);
for (int i = 1; i <= s; i++) {
scanf("%d %d %d", &x, &y, &t);
key[x][y] |= (1 << t);
}
memset(dis, 0x3f, sizeof(dis));
dis[1][1][key[1][1]] = 0;
vis[1][1][key[1][1]] = true;
q.push(make_pair(make_pair(1, 1), key[1][1]));
while (!q.empty()) {
cur = q.front(); q.pop();
x = cur.first.first;
y = cur.first.second;
k = cur.second;
for (int i = 0; i < 4; i++) {
int nx = x + dx[i], ny = y + dy[i];
if (nx >= 1 && nx <= n && ny >= 1 && ny <= m && (k & gate[x][y][nx][ny]) == gate[x][y][nx][ny]) {
int nk = k | key[nx][ny];
if (!vis[nx][ny][nk]) {
vis[nx][ny][nk] = true;
dis[nx][ny][nk] = dis[x][y][k]+1;
q.push(make_pair(make_pair(nx, ny), nk));
}
}
}
}
ans = dis[0][0][0];
for (int i = 0; i < (1 << 11); i++) ans = min(ans, dis[n][m][i]);
if (ans == dis[0][0][0]) cout << "-1\n";
else cout << ans << endl;
return 0;
}
编译结果
compiled successfully
time: 7ms, memory: 1876kb, score: 100, status: Accepted
> test 1: time: 0ms, memory: 1876kb, points: 10, status: Accepted
> test 2: time: 0ms, memory: 1876kb, points: 10, status: Accepted
> test 3: time: 1ms, memory: 1876kb, points: 10, status: Accepted
> test 4: time: 1ms, memory: 1876kb, points: 10, status: Accepted
> test 5: time: 1ms, memory: 1876kb, points: 10, status: Accepted
> test 6: time: 1ms, memory: 1876kb, points: 10, status: Accepted
> test 7: time: 0ms, memory: 1876kb, points: 10, status: Accepted
> test 8: time: 2ms, memory: 1876kb, points: 10, status: Accepted
> test 9: time: 1ms, memory: 1876kb, points: 10, status: Accepted
> test 10: time: 0ms, memory: 1876kb, points: 10, status: Accepted
C. 大学生活
题目描述:
大学的课程是在不同教室上的,需要同学们在不同时间自己去上课。
小Q 当前位置在 \(A\),他下一门课在 \(B\) 处上,他想知道最短多少次操作才能到达 \(B\)。
一次操作可以是:朝当前方向走一步、向左转、向右转、向后转。
初始时小Q可以任选一个朝向。
输入格式:
第一行包含一个整数 \(n\),表示大学的边长。
接下来 \(n\) 行,每行一个长度为 \(n\) 的字符串。'x' 表示障碍物,'.' 表示道路。
输出格式:
输出一个整数表示答案,走不到则输出 \(-1\)。
样例输入:
3
.xA
...
Bx.
样例输出:
6
数据规模:
\(2 \le N \le 100\)。
点击查看代码
#define MAXN 105
int n, ans = -1;
int xy[4][2] = { {1, 0}, {0, 1}, {-1, 0}, {0, -1} };
char mp[MAXN][MAXN];
bool vis[MAXN][MAXN][4];
struct node{ int x, y, step, p; };
void bfs(int x,int y){
queue<node> q;
q.push({x, y, 0, -1});
while(q.size()) {
node t = q.front();
if(mp[t.x][t.y] == 'B') {
ans = t.step;
return;
}
q.pop();
for(int i = 0; i < 4; i ++) {
int xx = t.x + xy[i][0], yy = t.y + xy[i][1];
if(xx >= 1 && xx <= n && yy >= 1 && yy <= n && mp[xx][yy] != 'x' && vis[xx][yy][i] == 0) {
if(t.p == -1 || t.p == i) {
vis[xx][yy][i] = 1;
q.push({xx, yy, t.step + 1, i});
}
else
q.push({t.x, t.y, t.step + 1, i});
}
}
}
}
int main(){
cin >> n;
int x, y;
for(int i = 1; i <= n; i ++)
for(int j = 1; j <= n; j ++) {
cin >> mp[i][j];
if(mp[i][j] == 'A') x = i, y = j;
}
bfs(x, y);
cout << ans << endl;
return 0;
}
编译结果
compiled successfully
time: 12ms, memory: 3600kb, score: 100, status: Accepted
> test 1: time: 0ms, memory: 3492kb, points: 10, status: Accepted
> test 2: time: 2ms, memory: 3544kb, points: 10, status: Accepted
> test 3: time: 2ms, memory: 3428kb, points: 10, status: Accepted
> test 4: time: 1ms, memory: 3420kb, points: 10, status: Accepted
> test 5: time: 1ms, memory: 3432kb, points: 10, status: Accepted
> test 6: time: 2ms, memory: 3444kb, points: 10, status: Accepted
> test 7: time: 1ms, memory: 3600kb, points: 10, status: Accepted
> test 8: time: 2ms, memory: 3440kb, points: 10, status: Accepted
> test 9: time: 0ms, memory: 3436kb, points: 10, status: Accepted
> test 10: time: 1ms, memory: 3360kb, points: 10, status: Accepted