只写部分题目。
A. Rudolph and Cut the Rope
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 2e5 + 5;
int t, n, a[N], b[N];
signed main() {
cin >> t;
while (t--) {
cin >> n;
int res = 0;
for (int i = 1; i <= n; i++) cin >> a[i] >> b[i];
for (int i = 1; i <= n; i++) {
if (a[i] > b[i]) {
res++;
}
}
cout << res << endl;
}
}
B. Rudolph and Tic-Tac-Toe
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 2e5 + 5;
char a[5][5];
signed main() {
int t;
cin >> t;
while (t--) {
for (int i = 1; i <= 3; i++) {
for (int j = 1; j <= 3; j++) cin >> a[i][j];
}
if (a[1][1] == a[1][2] && a[1][2] == a[1][3] && a[1][1] != '.') cout << a[1][1] << endl;
else if (a[2][1] == a[2][2] && a[2][2] == a[2][3] && a[2][1] != '.') cout << a[2][1] << endl;
else if (a[3][1] == a[3][2] && a[3][2] == a[3][3] && a[3][1] != '.') cout << a[3][1] << endl;
else if (a[1][1] == a[2][1] && a[2][1] == a[3][1] && a[1][1] != '.') cout << a[1][1] << endl;
else if (a[1][2] == a[2][2] && a[2][2] == a[3][2] && a[1][2] != '.') cout << a[1][2] << endl;
else if (a[1][3] == a[2][3] && a[2][3] == a[3][3] && a[1][3] != '.') cout << a[1][3] << endl;
else if (a[1][1] == a[2][2] && a[2][2] == a[3][3] && a[1][1] != '.') cout << a[1][1] << endl;
else if (a[1][3] == a[2][2] && a[2][2] == a[3][1] && a[1][3] != '.') cout << a[1][3] << endl;
else puts("DRAW");
}
}
C. Rudolf and the Another Competition
貌似没什么好说的,不懂场上怎么这么多人被 hack。
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 2e5 + 5;
int n, m, h;
vector<int> a[N];
struct edge {
int tot, f, id;
}rk[N];
bool cmp(edge x, edge y) {
if (x.tot == y.tot) {
if (x.f == y.f) return x.id < y.id;
return x.f < y.f;
}
return x.tot > y.tot;
}
signed main() {
int t;
cin >> t;
while (t--) {
cin >> n >> m >> h;
for (int i = 1; i <= n; i++) {
a[i].clear();
for (int j = 1; j <= m; j++) {
int x;
cin >> x;
a[i].push_back(x);
}
sort(a[i].begin(), a[i].end());
}
for (int i = 1; i <= n; i++) {
int sum = 0, tt = 0, res = 0;
for (auto j : a[i]) {
if (sum + j <= h) {
tt++;
sum += j;
res += sum;
}
}
rk[i] = {tt, res, i};
}
sort(rk + 1, rk + n + 1, cmp);
for (int i = 1; i <= n; i++) {
if (rk[i].id == 1) cout << i << endl;
}
}
}
D. Rudolph and Christmas Tree
这个题,把所有三角形面积相加再减去重叠部分即可。
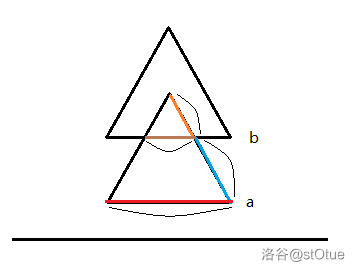
由相似知识得,黄边比蓝边等于 \(\dfrac{h-(b-a)}{(b-a)}\),则绿边比红边等于 \(\dfrac{h-(b-a)}{h}\)。根据题意,红边长为 \(d\),则绿边长为 \(d\times \dfrac{h-(b-a)}{h}\)。则重叠小三角形面积为 \(\dfrac{1}{2}\times d\times \dfrac{h-b+a}{h}\times (h-b+a)\)(不想整理了)。
代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 2e5 + 5;
int t, n, d, h;
double y[N], ans;
signed main() {
cin >> t;
while (t--) {
ans = 0;
cin >> n >> d >> h;
for (int i = 1; i <= n; i++) cin >> y[i], ans += 0.5 * d * h;
for (int i = 1; i < n; i++) {
if (y[i] + h > y[i + 1]) {
ans -= 0.5 * d * (h - y[i + 1] + y[i]) / h * (h - y[i + 1] + y[i]);
}
}
printf("%.8lf\n", ans);
}
}
E1. Rudolf and Snowflakes (simple version)
暴力呗。。。
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 2e5 + 5;
int t, n;
map<int, int> vis;
signed main() {
cin >> t;
n = 1e6;
for (int i = 2; i <= n; i++) {
int ans = 0, kk = 1, tt = 0;
for (int j = 1; j <= n; j++) {
ans += kk;
tt++;
kk *= i;
if (ans > n) break;
if (tt >= 3) vis[ans] = 1; // 这是个坑点,没看题的都会错
}
}
while (t--) {
cin >> n;
if (vis[n]) puts("Yes");
else puts("No");
}
}
E2. Rudolf and Snowflakes (hard version)
题意
给定 \(n(1\leq n\leq 10^{18})\),存不存在 \(k,p(k≥2,p≥2)\) 满足 \(1+k^2+k^3+...+k^p=n\)。
分析
考虑 \(p\) 的最大值:取 \(k\) 的最小值 \(2\),可求出 \(p\) 最大值约为 \(63\)。
考虑 \(k\) 的最大值:取 \(p\) 的最小值 \(2\),可求出 \(k\) 最大值约为 \(10^9\)。
既然 \(p\) 的范围不大,那么我们枚举 \(p\),因为 \(1+k^2+k^3+...+k^p\) 满足随着 \(k\) 增大则增大的性质,可以二分符合条件的 \(k\)。
代码
#include <bits/stdc++.h>
using namespace std;
#define int __int128
const int N = 2e5 + 5;
int t, n;
int read() {
char c = ' ';
int f = 1, x = 0;
while (c < '0' || c > '9') {
if (c == '-') f = -1;
c = getchar();
}
while (c >= '0' && c <= '9') {
x = x * 10 + c - '0';
c = getchar();
}
return x * f;
}
int check(int x, int p) {
__int128 ans = 0, kk = 1; // 这里会爆 long long,须开__int128
for (int i = 1; i <= p + 1; i++) {
ans += kk;
kk *= x;
if (ans > n) return 1; // 二分结果大于n
}
if (ans == n) return 2; // 二分结果等于n
else return 0; // 二分结果小于n
}
signed main() {
t = read();
while (t--) {
n = read();
int flg = 0;
for (int i = 2; i <= 63; i++) {
int l = 2, r = 1e9;
while (l < r) {
int mid = (l + r) >> 1;
int t = check(mid, i);
if (t == 1 || t == 2) r = mid; // 如果二分结果大于等于n,调整右端点
else l = mid + 1; // 否则调整左端点
}
if (check(l, i) == 2) { // 最后需要检查答案是否恰好为n
flg = 1;
break;
}
}
if (flg) puts("Yes");
else puts("No");
}
}
G. Rudolf and CodeVid-23
把当前的病情状况看成点,吃药前和吃药后的病况看成一条边的两个端点,药的服用天数看成边权。那么跑最短路,从初始病情状态到最终全为 \(0\) 的最短距离就是答案。
假设当前病情为 \(x\),药的功效为 \(y\),药的副作用为 \(z\)。那么吃完药后病情变为 \(x⊕(x\&y)|z\)。
看不懂?那补充一下了:设有两个集合 \(A,B\)
- 集合 \(A\) 和 \(B\) 的交集,即求出 \(A,B\) 都有的部分,表示为 \(A\&B\)。
- 集合 \(A\) 和 \(B\) 的并集,即把 \(A,B\) 合并起来,表示为 \(A|B\)。
- 集合 \(A\) 和 \(B\) 的差集,即从 \(A\) 中去掉 \(A,B\) 都有的部分,表示为 \(A⊕(A\&B)\)。
换到这题来,药的功效即为差集,药的副作用即为并集。
代码
#include <bits/stdc++.h>
using namespace std;
#define PII pair<int, int>
#define int long long
const int N = 12, M = 1003;
int T, n, m, d[M], use[M], unuse[M], dist[1 << N], st[1 << N];
char a[N], gd[M][N], ungd[M][N];
int en, first[1 << N];
struct edge {
int e, d, next;
}ed[(1 << N) * M];
void add_edge(int s, int e, int d) {
en++;
ed[en].e = e, ed[en].d = d;
ed[en].next = first[s];
first[s] = en;
}
void dij(int s) {
fill(dist, dist + (1 << N) - 4, 1e18);
memset(st, 0, sizeof st);
priority_queue<PII, vector<PII>, greater<PII> > q;
q.push({0, s});
dist[s] = 0;
while (q.size()) {
auto t = q.top();
q.pop();
int u = t.second;
if (st[u]) continue;
st[u] = 1;
for (int p = first[u]; p; p = ed[p].next) {
int e = ed[p].e, d = ed[p].d;
if (dist[e] > dist[u] + d) {
dist[e] = dist[u] + d;
q.push({dist[e], e});
}
}
}
}
signed main() {
cin >> T;
while (T--) {
en = 0;
memset(first, 0, sizeof first);
cin >> n >> m;
cin >> a;
int st = 0;
for (int i = 0; i < n; i++) {
if (a[i] == '1') st += (1 << (n - 1 - i));
}
for (int i = 1; i <= m; i++) {
cin >> d[i];
cin >> gd[i] >> ungd[i];
use[i] = unuse[i] = 0;
}
for (int i = 1; i <= m; i++) {
for (int j = 0; j < n; j++) {
if (gd[i][j] == '1') use[i] += (1 << (n - 1 - j));
}
for (int j = 0; j < n; j++) {
if (ungd[i][j] == '1') unuse[i] += (1 << (n - 1 - j));
}
}
for (int i = 0; i < (1 << n); i++) {
int tmp = i;
for (int j = 1; j <= m; j++) {
tmp = i;
tmp = tmp ^ (tmp & use[j]);
tmp |= unuse[j];
add_edge(i, tmp, d[j]);
}
}
dij(st);
if (dist[0] != 1e18) cout << dist[0] << endl;
else puts("-1");
}
}