Rapid, Detail-Preserving Image Downscaling(快速的图像缩放技术)
该论文提出了一种基于卷积滤波器的算法,并确定滤波器的权值,使重要的细节保留在缩小比例的图像。更具体地说,它为更偏离局部图像邻域的像素分配更大的权重。
从信息论的角度来看,偏离中心像素的邻域的一些像素数据可能携带有价值的信息,也可能是噪声或超出奈奎斯特频率的信息。
根据Beghdadi等人[2013]的研究,人类视觉系统“近似于拉普拉斯边缘检测器和自适应低通滤波”。因此,一定程度的噪点和混叠是可以容忍的,而模糊会导致重要细节的丢失。
Kopf等人[2013]提出了一种基于联合双边滤波器的方法。对于每个输出像素,它们在输入图像中定义一个相应的区域。与纯分割相反,每个输入像素可能对输出像素的数量有加权贡献。
该论文算法首先计算原始图像的平滑、缩小版本作为引导图像。考虑到我们应专注于大图像的下采样尺度,基于box filter快速地完成。然后使用卷积滤波器从输入图像组装最终图像,该滤波器赋予与引导图像所表示的局部邻域不同的像素更多的权重。
算法步骤
前置步骤
1、原图$I$通过box filter,生成一个 box filterd,downscaled图降采样图$Id$,参数$d$表示降采样倍数;($Id$形成没有说明,这个是重点)
2、原图$I$中的像素$p$用$\Omega _{I}(p)$表示原图的矩形块像素映射到降采样图$Id$中;
3、暂定$d$是整数
4、$Id$用卷积公式处理得到$\tilde{I}$(模糊图),相当于对$I$做公式2滤波
这种近似比完全高斯近似快得多(特别是对于大d),并且给出非常相似的结果
5、

注:
1、box filter 与gaussian filter的结果图一些差别,gaussian filter结果图与文中的guidance image差别不大。
2、处理边缘像素,可以扩展
后续步骤
通过联合双边滤波器计算输出图像O。
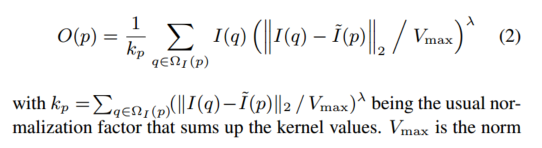
8bit数据下,$Vmax = \sqrt{3*255^{2}}$,将RGB数值归一化。
方程2与常规联合双边滤波器有两大区别:
首先,距离核不减小,而是随着清晰度的增加而增大,即它更倾向于I帽的局部像素邻域的差异
其次,空间核不是高斯函数,是矩形函数,$\Omega _{I}(p)$内为1,在其他地方为0
参数讨论
1、$\lambda$参数影响讨论,指数函数内是归一化数据,用$\lambda$求幂,参数小于1增强,大于1减少
2、结果取决于自身像素和$\Omega _{I}(p)$内周围像素,通过$Kp$连接
3、当$λ= 0$时,所有像素被统一地(与它们的清晰度无关)赋值为1的范围核,权重$1/k_{p}=1/(d^{2})$,此时本文filter等同box filter。
4、λ= 0.5或者1

觉得本文对您有一点帮助,欢迎讨论、点赞、收藏,您的支持激励我多多创作。