Splay:平衡树的一种,学名伸展树。
平衡树首先是一棵二叉搜索树(BST),满足性质:中序遍历单调递增。
根据这个性质,很容易在一棵 BST 上完成以下操作:插入一个数,查询一个数的排名,查询给定排名的数,删除一个数。
BST 可能是不平衡的,即左右子树相差很大。Splay 均摊后是平衡的,即时间复杂度均摊 \(O(n\log n)\)。
Splay 的基本操作是旋转rotate和伸展splay。
rotate算是大部分平衡树都有的一个操作,它的作用是将一个结点由儿子变成父亲,且不改变 BST 的性质。旋转分左旋和右旋,可以理解为对左儿子右旋,对右儿子左旋(实际不用区分)。捞两张图来说明:
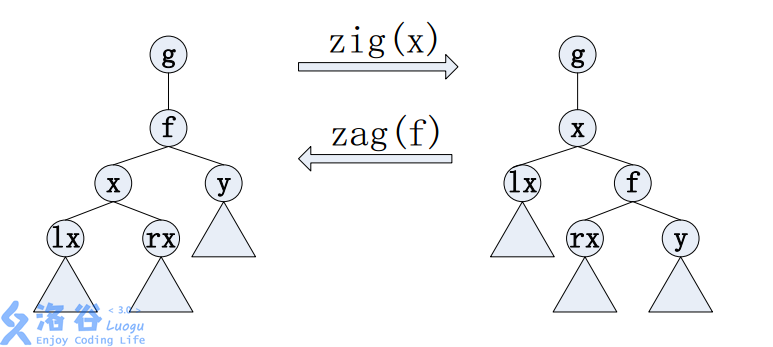
代码实现:
int rt,tot,fa[N],ch[N][2],val[N],cnt[N],siz[N];
//rt表示平衡树的根,fa表示结点的父亲,ch[u][0/1]表示u的左儿子/右儿子,val表示
//结点存储的值,cnt表示个数,siz表示子树大小
void push_up(int p){siz[p]=siz[ch[p][0]]+siz[ch[p][1]]+cnt[p];}
bool get(int p){return p==ch[fa[p]][1];}
void rotate(int x){//x是旋转中的儿子结点
int y=fa[x],z=fa[y],op=get(x)^1;
if(z)ch[z][get(z)]=x;//这句推荐写在前面。这里写后面没关系,但接下来LCT不行
ch[y][op^1]=ch[x][op];if(ch[x][op])fa[ch[x][op]]=y;//更新x的儿子
ch[x][op]=y;fa[y]=x;fa[x]=z;//更新x和y
push_up(y);push_up(x);//不要忘记更新结点信息
}
splay表示把一个点转到根。如果一直单旋复杂度不对,要使用双旋。双旋,即当 \(x\) 和 \(fa[x]\) 是同侧儿子时,先转 \(fa[x]\),再转 \(x\),否则转两次 \(x\)(也可能只能转一次,因为 \(fa[x]=rt\))。有些时候我们并不想把 \(x\) 转到根,那同样很容易。代码实现:
void splay(int x,int goal=0){//将x转到goal
for(int p=fa[x];p!=goal;p=fa[x]){
if(fa[p]!=goal)rotate(get(p)==get(x)?p:x);
rotate(x);//双旋
}if(!goal)rt=x;//不要忘记可能要更新根结点
}
特别的,Splay的删除可以直接把一个点转到根,然后删除,将其左子树的最小值(一路向左找儿子)转到根,并将原来的右子树接回去。代码实现:
void merge(int x,int y){
while(ch[x][1])x=ch[x][1];
splay(x);ch[x][1]=y;fa[y]=x;push_up(x);
}
void del(int v){
if(!find(v))return;
if(cnt[rt]>1){--cnt[rt],--siz[rt];return;}
int x=ch[rt][0],y=ch[rt][1];
fa[x]=fa[y]=0;clear(rt);
if(!x||!y){rt=x+y;return;}
merge(x,y);
}
Splay 的一个技巧是把点类似线段树的结点用,打各种各样的标记。只要在每次找点(加点,查询排名,查询值)的时候pushdown即可。然后用操作splay可以提取一段区间 \([l,r]\),这只要splay(l-1);splay(r+1,l-1),然后 \(r+1\) 的左子树就是区间 \([l,r]\)。例题:洛谷P3391 文艺平衡树
更多的例题可以看 Solution Set - Splay。
LCT:Link/Cut Tree。用来解决A+B problem动态树问题。这个问题中要维护一个森林,支持动态连边,删边和其它一些操作。
思想是做虚实链剖分,用 Splay 维护所有链(按照深度排序)。所谓的虚实链剖分,和重链剖分一样,都是给每个点选一条连向儿子的边作为重边/实边,然后维护这些链。不同之处在于实边完全可以随便选,反正Splay都可以维护。利用这一点,科学家发明了 LCT。
想象很多 Splay,每个维护一条实链。然后我们在一条链对应的 Splay 的根结点的父亲指向这条链原本的根结点。这就代表了一条虚边,它最重要的特点是“子认父,父不认子”。(建议把辅助树丢到一边去呢)
LCT 的核心操作包括打通Access和换根makeroot。
打通Access,即把一个点到根的路径上所有边更改为实边。只要从某个点开始,不断对它伸展,然后跳父亲,改儿子即可。不要问时间复杂度,问就是 Splay 保证。
换根makeroot,只要先打通再伸展。但注意此时左右子树需要调换,类似于“文艺平衡树”打标记即可。
剩下的连边link,提取路径split,删边cut都很好实现了,直接看代码叭。
void Access(int x){
for(int y=0;x;y=x,x=fa[x])
splay(x),ch[x][1]=y,push_up(x);
}
int findRoot(int p){
Access(p);splay(p);
while(ls)push_down(p),p=ls;
splay(p);return p;
}
//找一个点所在链的根,只要转到根后一路向左即可
void makeRoot(int p){Access(p);splay(p);make_tag(p);}
void split(int x,int y){makeRoot(x);Access(y);splay(y);}
bool link(int x,int y){
makeRoot(x);
if(findRoot(y)==x)return false;
//有时候题目不保证连接的边一定不成环,那就要判一下是否已经是根
fa[x]=y;return true;
}
void cut(int x,int y){split(x,y);ch[y][0]=fa[x]=0;push_up(y);}
//同样可能不保证删除的边存在,但最好直接开一个map记录,没必要整什么性质
