When a number is multiplied by itself, the resulting number is called as a square number. 

For example, when we multiply 5 by 5, we get 5² = 25. Here, 25 is a square number.

In geometry, the area of a square is the finest example of a square number. Area of a square = Side × Side = Side², because all the sides of a square are equal. This means the area of a square is always a square number.

Square numbers are always positive and they can never be negative because when a negative number is multiplied by the same negative number, it results in a positive number.

For example, (-7)² = -7 x -7 = 49 (two negative signs multiplied by each other result in a positive sign). When we multiply -7 by -7, the result is 49 and it is a positive square number. Here are some examples of square numbers.

2 x 2 = 4

-8 x -8 = 64

15 x 15 = 225

We observe the following properties through the patterns of square numbers.

Property 1 : 

In square numbers, the digits at the unit’s place are always 0, 1, 4, 5, 6 or 9. The numbers having 2, 3, 7 or 8 at its units' place are not perfect square numbers.

Property 2 :

If a number has 1 or 9 in the unit's place then its square ends in 1.

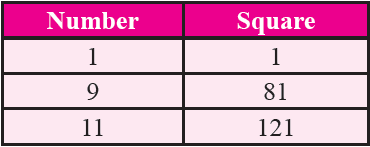
Property 3 :

If a number has 2 or 8 in the unit's place then its square ends in 4.

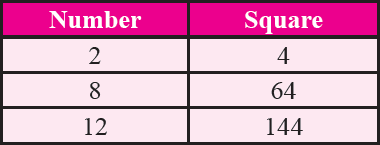
Property 4 :

If a number has 3 or 7 in the unit's place then its square ends in 9.

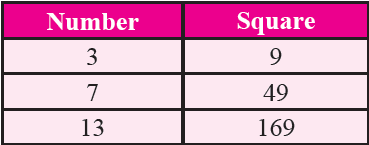
Property 5 :

If a number has 4 or 6 in the unit's place then its square ends in 6.

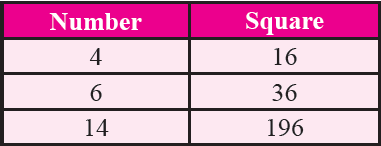
Property 6 :

If a number has 5 in the unit's place then its square ends in 5.

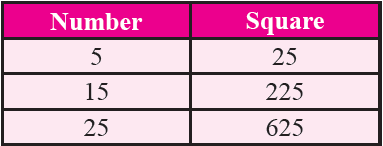
Property 7 :

Consider the following square numbers :

From the square numbers given above, we infer that

Property 8 :

Consider the following square numbers :

Therefore, 100 is a perfect square and 81000 is not a perfect square.

Property 9 :

Square of even numbers is always even. 

It has been illustrated in the table given below.

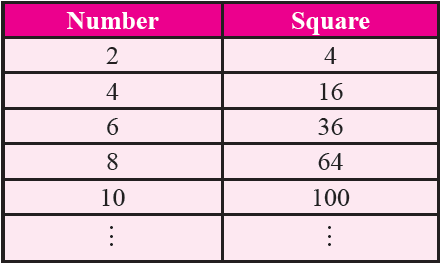
Property 10 :

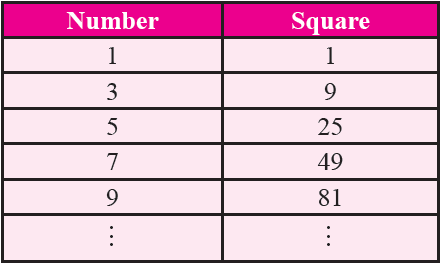
Square of odd numbers is always odd. 

It has been illustrated in the table given below.

From properties 9 and 10, we infer that

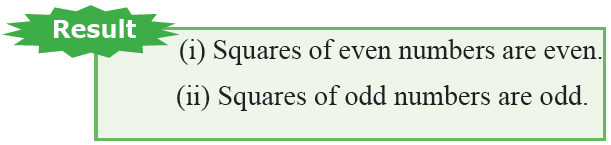
Some Interesting Patterns of Square Numbers

Addition of consecutive odd numbers :

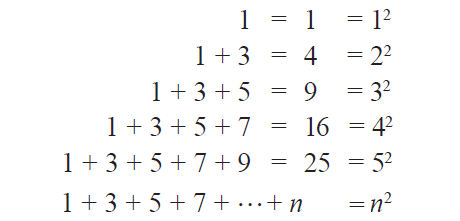
The above figure illustrates the result that the sum of the first n natural odd numbers is n².

And, square of a rational number a/b is given by

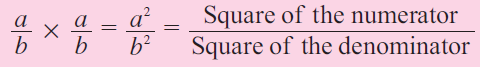
Kaprekar Numbers