首页 > 其他分享 >二分

二分

时间：2023-07-11 18:35:07浏览次数：36  
标签：二分 fr return int mid lwl define

23.7.11 Day 2

二分

 这个二分模板好记欸。

while (l <= r) {
    int mid = (l + r) >> 1;
    if (check(mid)) l = mid + 1,ans = mid;
    else r = mid - 1;
}

Rest The Shades

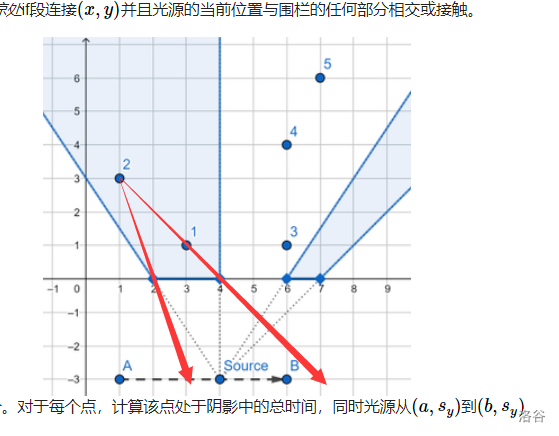
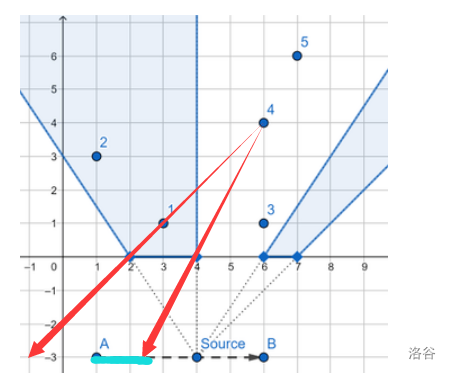
 前缀和记录，然后单独计算一下两头的线段，也就是蓝色那一段，用总的减不在里面的就可以。还有一点相似比。而且要记得把 \(min\) 和 \(max\) 改成 \(double\) ！

 还没有过，现在cf寄了，样例过了。

 好好好过了

#include<bits/stdc++.h>
#define kg putchar(' ')
#define ch puts("")
#define wj puts("0.000000000000000")
#define se second
#define fi first
using namespace std;
typedef long long lwl;
typedef pair<int,int> pii;

const int N = 2e5 + 5, inf = 0x3f3f3f3f;
double zero = 1e-8;

int n,Q;
int wl[N],wr[N];
lwl sum[N];
int a,b,wy;

lwl fr(){
    lwl x = 0, flag = 1;
    char t;
    t = getchar();
    while (t < 48 || t > 57){
        if (t == '-') flag = -1;
        t = getchar();
    }
    while (t >= 48 && t <= 57){
        x = x * 10 + t - 48;
        t = getchar();
    }
    return x*flag;
}

void fw(lwl x){
    if (x < 0) putchar('-'),x = -x;
    if (x > 9){
        fw(x / 10);
    }
    putchar(x % 10 + '0');
    return ;
}

int main(){
    wy = fr(),a = fr(),b = fr();
    int len = b - a;
    n = fr();
    for (int i = 1; i <= n; i ++) {
        wl[i] = fr();
        wr[i] = fr();
        sum[i] = sum[i - 1] + wr[i] - wl[i];
    }
    Q = fr();
    int x,y;
    double ans;
    while (Q --) {
        x = fr(),y = fr();
        double k = 1.0 * y / (y + abs(wy));
        
        double dxa = (a - x) * k + x,dxb = (b - x) * k + x;
        
        if (dxb <= wl[1] || dxa >= wr[n]) {
            wj;
            continue;
        }
        
        double L,R;
        int l = 1,r = n;
        while (l <= r) {
            int mid = (l + r) >> 1;
            if (wr[mid] <= dxa + zero) l = mid + 1;
            else r = mid - 1;
        }
        L = sum[l];
        L -= min((double)wr[l] - wl[l], wr[l] - dxa);
        
        l = 1,r = n;
        while (l <= r) {
            int mid = (l + r) >> 1;
            if (wl[mid] < dxb - zero) l = mid + 1;
            else r = mid - 1;
        }
        R = sum[n] - sum[r - 1];
        R -= min((double)wr[r] - wl[r], dxb - wl[r]);
        
        ans = 1.0 * len * (sum[n] - R - L) / (dxb - dxa);
        printf("%.15f",ans);
        ch;
    }
    return 0;
}

Rain of Fire

 不是杭师大是被codeforces拉黑了吗，今天做了两道codeforces的题，但是codeforces可以登上去的时间只有一个小时不到，到底什么时候可以交啊！

 代码写了，样例叶过了，但是没办法提交不知道对不对，交了之后再贴上来

 好好好过了过了过了，现在每次都争分多秒交 \(codeforces\)

#include<bits/stdc++.h>
#define kg putchar(' ')
#define ch puts("")
#define wj puts("-1")
#define se second
#define fi first
using namespace std;
typedef long long lwl;
typedef pair<int,int> pii;

const int N = 1e3 + 5, inf = 0x3f3f3f3f;

int n;
pii w[N];
map<pii,int> flag;
int h[N];
int id[5];
int a;

lwl fr(){
	lwl x = 0, flag = 1;
	char t;
	t = getchar();
	while (t < 48 || t > 57){
		if (t == '-') flag = -1;
		t = getchar();
	}
	while (t >= 48 && t <= 57){
		x = x * 10 + t - 48;
		t = getchar();
	}
	return x*flag;
}

void fw(lwl x){
	if (x < 0) putchar('-'),x = -x;
	if (x > 9){
		fw(x / 10);
	}
	putchar(x % 10 + '0');
	return ;
}

int min(int a,int b){
	if (a > b) return b;
	return a;
}

int max(int a,int b){
	if (a < b) return b;
	return a;
}

int dis(int i,int j) {
	return max(abs(w[i].fi- w[j].fi),abs(w[i].se - w[j].se));
}

int find(int x) {
	if (h[x] != x) h[x] = find(h[x]);
	return h[x];
}

bool check(int k) {
	for (int i = 1; i <= n; i ++) {
		h[i] = i;
	}
	for (int i = 1; i <= n; i ++) {
		for (int j = 1; j < i; j ++) {
			if (w[i].fi != w[j].fi && w[i].se != w[j].se)
				continue;
			if (dis(i,j) > k) continue;
			int ha = find(i),hb = find(j);
			if (ha != hb) {
				h[ha] = hb;
			}
		}
	}
	int cnt = 0;
	for (int i = 1; i <= n; i ++) {
		if (i == find(i)) {
			cnt ++;
			id[cnt] = i;
		}
	}
	if (cnt == 1) return true;
	if (cnt > 4) return false;
	if (cnt == 2) {
		for (int i = 1; i <= n; i ++) {
			for (int j = 1; j < i; j ++) {
				if (find(i) == find(j)) continue;
				if (dis(i,j) <= k)
						return true;
				if (w[i].se == w[j].se && 
					abs(w[i].fi - w[j].fi) <= 2 * k)
						return true;
				if (w[i].fi == w[j].fi &&
					abs(w[i].se - w[j].se) <= 2 * k)
						return true;
			}
		}
		return false;
	}
	if (cnt == 3) {
		int u[4] = {0,1,2,3};
		for (int qwq = 1; qwq <= 3; qwq ++) {
			swap(u[1],u[qwq]);
			a ++;
			for (int i = 1; i <= n; i ++) {
				if (find(i) != id[u[1]]) continue;
				for (int j = 1; j <= n ; j ++) {
					if (find(j) != id[u[2]]) continue;
					if (dis(i,j) <= k) {
						flag[{w[i].fi,w[j].se}] = a;
						flag[{w[j].fi,w[i].se}] = a;
					}
				}
			}
			for (int i = 1; i <= n; i ++) {
				if (find(i) != id[u[1]]) continue;
				for (int j = 1; j <= n; j ++) {
					if (find(j) != id[u[3]]) continue;
					if (dis(i,j) > k) continue;
					if (flag[{w[i].fi,w[j].se}] == a ||
						flag[{w[j].fi,w[i].se}] == a)
						return true;
				}
			}
		}
		return false;
	}
	if (cnt == 4) {
		int u[5] = {0,1,2,3,4};
		for (int qwq = 1; qwq <= 2; qwq ++) {
			a ++;
			swap(u[2],u[3]);
			for (int i = 1; i <= n; i ++) {
				if (find(i) != id[u[1]]) continue;
				for (int j = 1; j <= n; j ++) {
					if (find(j) != id[u[2]]) continue;
					if (dis(i,j) <= k) {
						flag[{w[i].fi,w[j].se}] = a;
						flag[{w[j].fi,w[i].se}] = a;
					}
				}
			}
			for (int i = 1; i <= n; i ++) {
				if (find(i) != id[u[3]]) continue;
				for (int j = 1; j <= n; j ++) {
					if (find(j) != id[u[4]]) continue;
					if (dis(i,j) > k) continue;
					if (flag[{w[i].fi,w[j].se}] == a ||
						flag[{w[j].fi,w[i].se}] == a)
						return true;
				}
			}
		}
		return false;
	}
	return false;
}

int main(){
	n = fr();
	for (int i = 1; i <= n; i ++) {
		w[i].fi = fr();
		w[i].se = fr();
	}
	for (int i = 1; i <= n; i ++) {
		h[i] = i;
	}
	int cnt = n;
	for (int i = 1; i <= n; i ++) {
		for (int j = 1; j < i; j ++) {
			if (w[i].fi != w[j].fi && w[i].se != w[j].se)
				continue;
			int ha = find(i),hb = find(j);
			if (ha != hb) {
				cnt --;
				h[ha] = hb;
			}
		}
	}
	if (cnt > 2) {
		wj;
		return 0;
	}
	int l = 0,r = 2e9 + 1;
	while (l <= r) {
		int mid = ((lwl)l + r) / 2;
		if (check(mid)) r = mid - 1;
		else l = mid + 1;
	}
	fw(l);
	return 0;
}

练习

 三道二分，真是二分复建练习。考的时候只做了两道，还有一道是看了 Richard_H 之后写的，最后一题骗分骗了7分

 今天有自己的笔记本可以登QQ，群里聊天聊飞了。最后一题太长了而且也没有什么时间看了，就输出了个样例然后随便输了个数，有七分的高分！

A.奇怪的矩阵

 因为询问的时候都是以列作为单位的，所以说一开始先将所有数排序并且去重，我用的是 \(set\) ，因为不太习惯用 \(unique\)

 然后算这个去重完的数组差分，也就是相邻的两个数之间的距离，也就是说这两个数经过一段距离后数字会重合。然后再对差分数组排个序，最后对这个差分数组求个前缀和，这样后面直接用就可以了。这里的前缀和就是如果距离超过了当前的差分值，那么这些行提供的贡献就是固定的 \(sum\) 值

 最后对于每次询问，都把它转化成区间形式，因为这个区间左右移动时，中间的不同的数的数量是不会变的。然后对于这个区间二分一下当前区间在差分数组的哪个位置，这里的二分就相当于手写 \(lowerbound\)

 最后再针对没有完全包括的区间单独算一下就可以了。

#include<bits/stdc++.h>
#define kg putchar(' ')
#define ch puts("")
using namespace std;
typedef long long lwl;

const int N = 1e5 + 5, inf = 0x3f3f3f3f;
const lwl m = 1e18;

int n;
lwl w[N];
map<lwl,lwl> h;
lwl cf[N];
lwl sum[N];

lwl fr(){
	lwl x = 0, flag = 1;
	char t;
	t = getchar();
	while (t < 48 || t > 57){
		if (t == '-') flag = -1;
		t = getchar();
	}
	while (t >= 48 && t <= 57){
		x = x * 10 + t - 48;
		t = getchar();
	}
	return x*flag;
}

void fw(lwl x){
	if (x < 0) putchar('-'),x = -x;
	if (x > 9){
		fw(x / 10);
	}
	putchar(x % 10 + '0');
	return ;
}

int main(){
	freopen("qwq.in","r",stdin);
	set<int> s;
	n = fr();
	for (int i = 1; i <= n; i ++) {
		s.insert(fr());
	}
	n = s.size();
	int idx = 0;
	for (auto i : s) {
		w[++ idx] = i;
	}
	for (int i = 1; i < n; i ++) {
		cf[i] = w[i + 1] - w[i];
	}
	sort(cf + 1,cf + n);
	for (int i = 1; i <= n; i ++) {
		sum[i] = sum[i - 1] + cf[i];
	}
	int Q = fr();
	while (Q --) {
		lwl l = fr(),r = fr();
		lwl y = r - l + 1;
		l = 1,r = idx;
		while (l <= r) {
			lwl mid = (l + r) >> 1;
			if (cf[mid] < y) l = mid + 1;
			else r = mid - 1;
		}
		if (r == n) r = n - 1;
		lwl ans = (n - r) * y + sum[r];
		fw(ans);
		ch;
	}
	return 0;
}

B.区间加法

 考虑贪心加二分。二分就是二分答案，然后这里二分答案的时候不能直接用 \(1e14\) ，不然会 \(TLE\) ，因为这里给的范围是 \(\sum\) ，所以我们对每一组数据都求一遍最大值。

 在 \(check\) 函数里面，求当前答案是否符合的时候，这里用的是树状数组，但是复杂度好像有点问题，可以直接标记用前缀和做，但还我懒得写了，如果改做法可以省掉一个 \(\log n\)

 但是这一题的数据好像不是很强，如果最大值取 \(1e8\) 都可以做，真是让人大吃一惊。

#include<bits/stdc++.h>
#define kg putchar(' ')
#define ch puts("")
#define wj puts("-1")
#define se second
#define fi first
using namespace std;
typedef long long lwl;
typedef pair<int,int> pii;

const int N = 2e5 + 100, inf = 0x3f3f3f3f;

priority_queue<int> q;
int n,m,k,b;
lwl w[N];
pii qj[N];
lwl tr[N];

lwl fr(){
	lwl x = 0, flag = 1;
	char t;
	t = getchar();
	while (t < 48 || t > 57){
		if (t == '-') flag = -1;
		t = getchar();
	}
	while (t >= 48 && t <= 57){
		x = x * 10 + t - 48;
		t = getchar();
	}
	return x*flag;
}

void fw(lwl x){
	if (x < 0) putchar('-'),x = -x;
	if (x > 9){
		fw(x / 10);
	}
	putchar(x % 10 + '0');
	return ;
}

lwl lowbit(lwl a) {
	return a & -a;
}

void add(int x,lwl k) {
	while (x <= n + 1) {
		tr[x] += k;
		x += lowbit(x);
	}
}

lwl sum(int x) {
	lwl ans = 0;
	while (x) {
		ans += tr[x];
		x -= lowbit(x);
	}
	return ans;
}

void change(int l,int r) {
	add(l,b);
	add(r + 1,-b);
}

bool check(lwl mid) {
	while (q.size()) q.pop();
	memset(tr,0,sizeof tr);
	queue<int> qq;
	for (int i = 1; i <= n; i ++) {
		if (w[i] < mid) qq.push(i);
	}
	int cnt = 0;
	int u = 1;
	while (qq.size()) {
		auto t = qq.front();
		qq.pop();
		
		while (u <= m && qj[u].fi <= t) {
			q.push(qj[u].se);
			u ++;
		}
		
		while (w[t] + sum(t) < mid) {
			cnt ++;
			if (cnt > k) return false;
			if (!q.size()) return false;
			
			auto tt = q.top();
			q.pop();
			
			change(t,tt);
		}
	}
	return true;
}

int main(){
	//freopen("qwq.in","r",stdin);
	int T = fr();
	while (T --) {
		n = fr(),m = fr(),k = fr(),b = fr();
		for (int i = 1; i <= n; i ++) {
			w[i] = fr();
		}
		for (int i = 1; i <= m; i ++) {
			qj[i].fi = fr();
			qj[i].se = fr();			
		}
		sort(qj + 1,qj + 1 + m);
		lwl l = 0,r = 1e9;
		while (l <= r) {
			lwl mid = (l + r) >> 1;
			if (check(mid)) l = mid + 1;
			else r = mid - 1;
		}
		fw(r);
		ch;
	}
	return 0;
}

标签：二分,fr,return,int,mid,lwl,define
From： https://www.cnblogs.com/jingyu0929/p/17545621.html

相关文章

  • poj 1064 高精度 二分
    CablemasterTimeLimit: 1000MSMemoryLimit: 10000KTotalSubmissions: 32191Accepted: 6888DescriptionInhabitantsoftheWonderlandhavedecidedtoholdaregionalprogrammingcontest.TheJudgingCommitteehasvolunteeredandhaspromisedtoorganizethe......
  • 浮点数二分模板
    题目给定一个浮点数$n$，求它的三次方根。输入格式共一行，包含一个浮点数$n$。输出格式共一行，包含一个浮点数，表示问题的解。注意，结果保留$6$位小数。数据范围$−10000≤n≤10000$输入样例：$1000.00$输出样例：$10.000000$思路浮点数二分可以直接分,无需考虑边界情况......
  • 整体二分学习笔记
    整体二分引入对于一堆询问，如果每个单独的询问都可以二分解决的话，时间复杂度为\(O(NM\logN)\)，但实际上每次二分都会有一些残留信息被我们扔掉，如果我们将所有询问一起二分，就可以最大时间的减小复杂度。讲解经典例题：区间第k大给定一个序列a和一个整数S，有2种操作：1.将a......
  • 6312: 河中跳房子 二分
    描述 每年奶牛们都要举办各种特殊版本的跳房子比赛，包括在河里从一个岩石跳到另一个岩石。这项激动人心的活动在一条长长的笔直河道中进行，在起点和离起点L远(1≤L≤1,000,000,000)的终点处均有一个岩石。在起点和终点之间，有N(0≤N≤50,000)个岩石，每个岩石与起点的距......
  • 6307: 网线主管 二分/分治
    描述 仙境的居民们决定举办一场程序设计区域赛。裁判委员会完全由自愿组成，他们承诺要组织一次史上最公正的比赛。他们决定将选手的电脑用星形拓扑结构连接在一起，即将它们全部连到一个单一的中心服务器。为了组织这个完全公正的比赛，裁判委员会主席提出要将所有选手的电脑等距离......
  • 质谱数据，二分类，bp神经网络
    importnumpyasnpimportpandasaspdfromsklearn.model_selectionimporttrain_test_splitdata=pd.read_pickle('ICC_rms.pkl')df=pd.DataFrame(data)X=df.iloc[:,0:510].values#所有样本的x值，0-510列矩阵（1544，510）由此得出样本个数1544个，特征510y=df.iloc[:,5......
  • 二分法查找目标元素在数组中的索引
    /***给定一个n个元素有序的（升序）整型数组nums和一个目标值target，写一个函数搜索nums中的target，*如果目标值存在返回下标，否则返回-1。*输入:nums=[-1,0,3,5,9,12],target=9*输出:4*解释:9出现在nums中并且下标为4......
  • STL-二分查找函数
    binary_serch:查找某个元素是否出现，返回bool型lower_bound:查找第一个>=某个元素的位置upper_bound:查找第一个>某个元素的位置binary_search(beg,end,val)返回一个bool变量，以二分法检索的方式在[beg,end]之间查找val，找到返回true，找不到返回false。lower_bound（beg,end,va......
  • 算法——二分查找
    1、在有序数组中查找元素的第一个和最后一个位置1classSolution{2publicint[]searchRange(int[]nums,inttarget){3intleftindex=binarySearch(nums,target);4intrightindex=binarySearch(nums,target+1)-1;5if(leftindex=......
  • 二分算法学习笔记与总结
    二分算法学习笔记与总结目录二分二分原理整数二分二分查找原理二分查找模板模板一模板二二分查找用法题目1（模板）（二分查找）题目大意题目分析CODE题目2（运用）（二分查找）题目大意题目分析CODESTL中的二分查找lower_bound()upper_bound()浮点二分浮点数二分模板浮点数二分答案模板题目......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99