二叉搜索树

二叉搜索树

二叉搜索树（Binary Search Tree，BST）是指一颗空树或者有下列性质的二叉树：

• 若任意节点的左子树不为空，那么左子树上所有节点的值均小于它的根节点的值；
• 若任意节点的右子树不为空，那么右子树上所有节点的值均小于它的根节点的值；
• 任意节点的左、右子树也分别为二叉搜索树；

二叉树的定义是从一个递归的角度来定义的，验证二叉树其实很简单，即中序遍历二叉树，节点的值从严格递增。换言之，二叉搜索树也可以定义成中序遍历时节点值严格递增的二叉树。

BST 的删除

对树的定义，我们采取 Leetcode 中的定义：

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode() :
        val(0), left(nullptr), right(nullptr) {
    }
    TreeNode(int x) :
        val(x), left(nullptr), right(nullptr) {
    }
    TreeNode(int x, TreeNode *left, TreeNode *right) :
        val(x), left(left), right(right) {
    }
};

首先，我们定义两个辅助函数 TreeNode *delMax(TreeNode *root, int key); 和 TreeNode *delMin(TreeNode *root, int key);，分别表示删除二叉树中的值最大的节点和值最小的节点。还需要辅助函数 int getMin(TreeNode *root); 和 int getMax(TreeNode *root)。

getMin 和 getMax 自不必多说，以 delMax 为例，都是利用递归进行处理，递归返回的是当前以 root 为根节点的树，删除了最大值之后的 root。递归终止条件即 root->right == nullptr，说明找到了树的最大值，此时返回 root->left。（以避免左子树不为空的情况，左子树为空则相当于返回了 nulltpr）

int getMax(TreeNode *root) {
    if (root->right == nullptr) {
        return root->val;
    }
    return getMax(root->right);
}

int getMin(TreeNode *root) {
    // 不考虑空树的情况
    if (root->left == nullptr) {
        return root->val;
    }
    return getMin(root->left);
}
TreeNode *delMax(TreeNode *root) {
    if (root == nullptr) {
        return root;
    }
    if (root->right == nullptr) {
        return root->left;
    }
    root->right = delMax(root->right);
    return root;
}
TreeNode *delMin(TreeNode *root) {
    if (root == nullptr) {
        return root;
    }
    if (root->left == nullptr) {
        return root->right;
    }
    root->left = delMin(root->left);
    return root;
}

那么，有了这几个辅助函数之后，我们要如何处理 BST 的删除节点呢。还是递归进行处理，递归返回的是将以当前节点为根节点的树删除 key 对应节点之后的根节点 root。

• 如果 key 小于当前节点值，那么递归删除左子树；
• 如果 key 大于当前节点值，那么递归删除右子树；
• 如果 key 等于当前节点值，分两种情况讨论：
  • 如果当前节点没有右子节点，那么返回当前节点的左子节点，即 return root->left;，这样也能处理左子树也为空的情况；
  • 如果当前节点的右子树不为空，那么我们将当前节点的值替换为右子树的最小值 val，val 相当于是满足 k > key 的最小的 k，然后对该右子树，执行 delMin。

当然，碰到 key 等于当前节点值的情况时，我们考虑左子节点也是可以的，与考虑右子节点是对称的。

TreeNode *del(int key, TreeNode *root) {
    if (root == nullptr) {
        return nullptr;
    }
    if (key < root->val) {
        root->left = del(key, root->left);
    } else if (key > root->val) {
        root->right = del(key, root->right);
    } else {
        // root->val == key
        if (root->right == nullptr) { // 没有右子树
            return root->left;
        }
        root->val = getMin(root->right);
        root->right = delMin(root->right);
    }
    return root;
}

BST 的时间复杂度分析

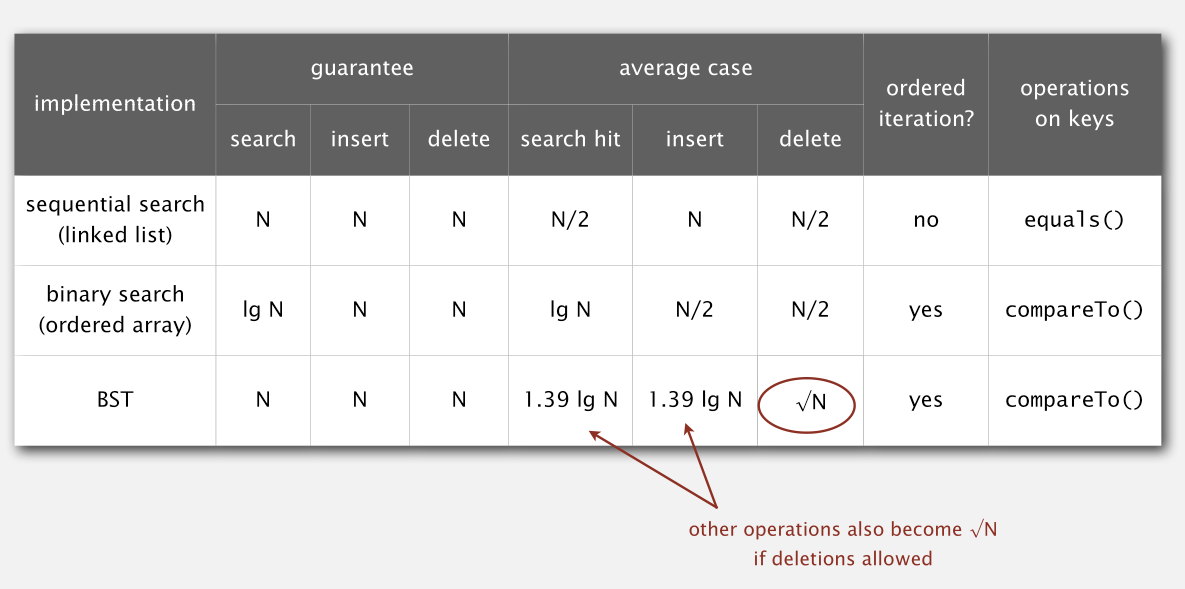
我们知道，假设 BST 没有额外的限制，那么，最坏情况下，它可能退化成一个有序链表，此时插入和查找的时间复杂度为 $O(n)$。

而我们如果利用插入节点，从无到有构造一棵 BST，并且插入的节点的值都是随机的，那么这棵 BST 的最大深度是 $O(\log n)$ 的（$n$ 为 BST 的节点数），即查找和插入的时间复杂度是 $O(\log n)$ 的。

但如果，我们除了执行随机节点的插入之外，还执行随机删除，那么 BST 的最大深度就会变成 $O(\sqrt n)$，即查找、插入、删除的时间复杂度变成了 $O(\sqrt n)$。