入门篇
字符串的基础概念及存储
基本概念不用多说,字符串就是一堆字符串在一起所构成的一个结构。
存储多有两种:
- 用c++自带的string
- 用字符数组char[]。(笔者习惯用这种方法)
如何输入/输出一个字符串?
//c++自带string
string s;
cin >> s;
cout << s;
//字符数组char
char s[];
scanf("%s", s);
printf("%s", s);
这算是最最基础的内容了,刚入门的小朋友也应该会。
字符串模拟
有关字符串的模拟。语法是大问题?
发现要读入空格,但是 cin 和 scanf 貌似都不能避免。可以使用 getline 函数。
基本定义
先了解一些形式化的字符串的定义。
\(\sum\) 代表字符集。字符集是一个建立了全序关系的集合。
\(s[l:r]\) 代表字符串 \(s\) 从 \(l\) 到 \(r\) 的这一段子串。本文字符串没有特殊说明均从 \(1\) 开始标号。
\(s[p_1,p_2,...p_m]\) 是子序列,是从 \(s\) 中提出这些位置的值并不改变相对顺序形成的字符串。
后缀 \(s[i:|s|]\),前缀 \(s[1:i]\)。
字典序,从前往后逐位比较字符大小,如果全部相等则长度较小的字典序更小。
回文串,正着读和反正读一样的字符串,即 \(s=s^{T}\)。
Hash
用来快速判断两个串是否相等。也就是把一个字符串映射成一个整数。
一般采用一个 \(\text{radix}\) 将串转成一个 \(\text{radix}\) 进制数,同时取模。
不要小看这个玩意,在大多数时候哈希可以减少码量和思维难度,是个不错的选择。
给定一个字符串 \(S\),求其可以被分解为多少个形如 \((AB)^rC\) 的形态。其中 \(F(A)<F(C)\),\(F(S)\) 表示字符串 \(S\) 中出现奇数次的字符的数量。
\(T\) 组询问,\(1\le T \le 5,1 \le |S| \le 2^{20}\)。
这里给出一个用字符串哈希做到 \(O(T(n\ln n+n\log{26})\) 的做法。线性做法在后面会提到。
考虑枚举 \(AB\) 然后枚举 \((AB)^r\),容易发现这是 \(O(n\ln n)\) 的。可以用字符串哈希来判断后面的部分是否也是 \(AB\)。接着将合法的 \(A\) 都加入树状数组,然后查询 \(C\) 即可,容易发现这是 \(O(n\ln n\log 26)\) 的。考虑 \(F(C)\) 只有两种取值,所以可以一起询问,复杂度正确。
如何卡掉字符串哈希?
卡自然溢出。
错误概率分析。
设模数是 \(M\),两字符串长度为 \(l\),\(f(s)\) 是字符串 \(s\) 的哈希函数。实际上这是 \(\mathbb{Z}_M[x]\) 上的一个多项式,依据选取的底数 b。
事实上,冲突等价于 \(b\) 是模意义方程的解,根据拉格朗日定理,这个解有 \(\Theta(|s|)\) 种,那随机情况下概率就约为 \(\frac{|s|}{M}\)。
更一般的分析,思考 \(k\) 个字符串都不相同的概率。
这些字符串的哈希值其实可以约看成 \(\mathbb Z_M\) 内的随机数。
那等价于 \(k\) 个随机数,互不相同的概率。
根据生日悖论,这个概率在 \(k<<M\) 的时候就能很大。
具体分析一下这个概率:\(1-\frac{M^{\underline{k}}}{M^k}\sim 1-e^{\frac{-k(k-1)}{2M}}\)。
字典树 Trie
Trie 树是一个树形结构,点称作状态,边称作转移,每个转移有一个字符。从根到某个节点的路径形成一个字符串。
字典树的构建非常简单,直接模拟暴力插入即可。复杂度为 \(O(\sum |S|)\)。现在你有一个指针 \(p\),指向 \(s[1:i]\) 这个前缀所代表的节点。如果存在一条转移边恰好是 \(s[i+1]\),那么直接将 \(p\) 转移过去。否则新建一个儿子和边,代表字符 \(s[i+1]\) 在 \(p\) 这个状态的转移。
检索字符串
貌似是最直接的一种应用。
给你 \(n\) 个字符串以及 \(m\) 个询问,每次询问需要回答:如果该询问的字符串没有在 \(n\) 个字符串里面出现过,输出“WRONG”,如果该询问的字符串出现过而且是第一次询问,输出“OK”,如果该询问的字符串出现过但不是第一次询问,输出“REPEAT”。
重复的可以考虑在trie上打标记。
01trie
给定一棵 \(n\) 个点的带权树,结点下标从 \(1\) 开始到 \(n\)。寻找树中找两个结点,求最长的异或路径。
异或路径指的是指两个结点之间唯一路径上的所有边权的异或。
考虑异或的性质,记 \(dis(a,b)\) 为路径异或值,\(1\) 为根,发现 \(dis(a,b)=dis(1,a)\bigoplus dis(1,b)\)。于是只需存一下 \(dis(1,u)\),然后枚举每个 \(u\),计算答案。
考虑贪心,从高位考虑。这时需要从高到底维护每个数的二进制表示,这可以用 01trie 来维护。查询如果能向当前位不同的子树走,就向那边走,否则没有选择。
01trie 维护全局异或和
01trie 还可用来维护异或和。支持插入、删除、全局加一。
从低到高维护 01trie。查询只需考虑这一层 \(1\) 的奇偶性。
考虑在trie上维护这么几个信息:
-
左儿子与右儿子
-
子树异或和 \(s\)
-
这个子树被插了几个数 \(w\)
然后考虑怎么做操作。
push_up
注意只需考虑 \(1\) 儿子的 \(w\) 的奇偶性。
void pushup(int now) {
w[now] = sxor[now] = 0;
if (son[now][0]) {
w[now] += w[son[now][0]];
sxor[now] ^= sxor[son[now][0]] << 1;
}
if (son[now][1]) {
w[now] += w[son[now][1]];
sxor[now] ^= (sxor[son[now][1]] << 1) | (w[son[now][1]] & 1);
}
}
- 插入
直接模拟,然后对叶子节点的 \(w\) 进行修改。
- 删除
和插入非常类似
void ins(int &now, int len, int v) {
if (!now) now = ++tot;
if (len > 20) {
w[now]++;
return;
}
ins(son[now][v & 1], len + 1, v >> 1);
pushup(now);
}
void del(int &now, int len, int v) {
if (len > 20) {
w[now]--;
return;
}
del(son[now][v & 1], len + 1, v >> 1);
pushup(now);
}
- 全局加一
思考每个数加一的过程——把最后一段 \(1\),变成 \(0\),然后把前面的 \(0\) 变成 \(1\)。这可以看成一个递归的过程。从低位往高位考虑。即把 \(0\) 和 \(1\) 的子树互换,然后递归进 \(1\) 的子树。
void add(int p) {
swap(son[p][0], son[p][1]);
if (son[p][0]) add(son[p][0]);
pu(p);
}
- trie的合并
可以把trie的合并与线段树合并看成一类。复杂度证明和写法都非常类似。
void merge(int x, int y) {
if (!x || !y) return x | y;
y -> x;
for (int i = 0; i < sigma; i++) {
son[x][i]=merge(son[x][i], son[y][i]);
}
return x;
}
VI 省选联考2020A卷 树
两道近乎板子的题。。。
可持久化trie
VII bzoj4212
给定 \(n\) 个字符串,\(m\) 次询问,每次询问给定两个串 \(s_1,s_2\),查询有多少个串的前缀是 \(s_1\),后缀是 \(s_2\)。
可持久化 trie 的方式和线段树一样,都是在修改的部分新建节点。
考虑对于每一个 \(s_1\) 插入 trie 树。然后要在 trie 树的子树内数数。经典结论子树的 dfs 序是一个区间,所以实际上是在区间里数数。这时直接用可持久化 trie 维护 \(s_2\) 即可。
复杂一点儿的应用
VIII AGC047B
不妨先求一个字符串 \(s\) 前有几个可以变成 \(s\),然后再倒过来求一遍一样的东西即可。除了字符串 \(s\) 的第一位其它位都必须紧贴前面的字符串的最后面。
那可以把所有前面的字符串反向建trie树,然后反过来在trie树上跑,如果不是第一位就走当前为,如果是第一位就随便走,如果走了当前为就返回。
可这样复杂度不对,考虑优化。对于每个trie树上的节点记录一下这个节点开始有几个字符串在前面有某个字符,然后如果是第一位就直接加上。那怎么维护呢,其实很简单,把插入变成递归插入,统计在回溯的时候记录一下当前哪些字符出现了,如果出现了某个字符回溯时就更新。
IX LG4036
因为有插入所以很难直接维护。考虑使用平衡树,用哈希值维护字符串之间的比较即可。查询是二分答案,平衡树维护子树哈希值。
X CF580E
众所周知,period 对应一个 border。所以如果一个区间 \([l,r]\) 有一个 \(r-l+1-d\) 的 吧 border 那么他就有一个长度为 \(d\) 的 period。而 border 的判断可以用哈希,接下来就是怎么维护哈希值了,其实就是一个很简单的区间修改,考虑使用线段树维护即可。
注意,千万不要在 cf 上用自然溢出,否则你会被卡得很惨。
XI AGC044C
观察到这个 \(N\) 非常的小。可以把所有三进制数插入一个 012trie,做类似 01trie 干的事情。对于此题的操作,交换 12 只需交换子树即可,又由于是静态的(最后才询问),所以打上懒惰标记即可。对于全局加一,发现他是直接省略高位,所以类似 01trie 的全局加一,找到一条以 2 结尾的链,然后以此与 0 交换。实现层面在每个结尾处记录一下这个地方是几号人即可。
XII CF464E
给定一张图,边权为 \(2^{x_i}\),求 \(s\to t\) 的最短路。\(1\le n,m,x_i\le 10^5\)。答案对 \(10^9+7\) 取模。
无法直接把路径长度记到数组里跑 dij。然后据说可以 Hash,我猜测是在比大小部分。但是我一直没有想到怎么去存储这个大数,于是我打开了题解,然后发现其实只要一个数据结构(线段树)就可以做了(因为要动态模拟)。
至于如何比较,其实就是比较两个二进制串的字典序,找到第一个不一样的位置,然后比较下一个位置即可。用线段树维护 Hash 值,时间复杂度 \(O(m\log n\log^2 x)\)。考虑在线段树上二分即可做到 \(O(m\log n\log x)\)
XIII CF504E
给定一棵 \(n\) 个节点的树,每个节点有一个小写字母。有 \(m\) 组询问,每组询问为树上 \(a \to b\) 和 \(c \to d\) 组成的字符串的最长公共前缀。
\(n \le 3 \times 10^5\),\(m \le 10^6\)。
感谢洛谷提供的翻译
因为这里是查询最长公共前缀,所以考虑使用二分+Hash来解决。首先找到 \(a,b\) 和 \(c,d\) 的 \(lca\),然后判断会不会转弯这里又有若干种(应该是四种)情况需要讨论。
貌似思路不是很难想但是代码貌似有点 ex(不是难写,只是单纯的烦)。
kmp
定义 字符串 border 为其前缀等于后缀的集合,也就是 \(S=\{i\mid i\in [1,|S|-1], s[1:i]=s[|S|-i+1:|S|]\}\)。
对于每个位置,统计 \(fail_i\) 为 \(s[1:i]\) 的最长 border,没有则为 \(0\)。
如果将 \(i\to fail_i\) 连一条边,会形成一条链。在求 \(fail_i\) 时显然所有 \(s[1:i]\) 的 border 都应该在 \(i-1\) 的那条链上。一个暴力的做法是直接在链上跳并判断。
下面来证明这个做法是正确的。考虑现在有一个势能函数 \(\Phi(n)\),每次更新最多只会增加一,而每次减少只会减少到 \(0\)。所以总的复杂度等于增加的长度和即为 \(O(n)\)。
利用 \(fail\) 数组,可以用类似的方法做字符串匹配。
kmp 自动机
定义 确定有限状态自动机(DFA)
对于每个状态,和字符集,都可以转移到另一个状态。
定义字符串每个位置为状态代表 \(s[:i]\),转移 \(ch_{i,c}\) 代表状态 \(i\) 加入字符 \(c\) 后的 border。可以利用 \(fail\) 数组在 \(O(n)\) 时间内构建 kmp 自动机。
XIV CF808G Anthem of Berland
给定 \(s\) 串和 \(t\) 串,其中 \(s\) 串包含小写字母和问号,\(t\) 串只包含小写字母。你需要给把每个问号变成一个小写字母,求出所有匹配中 \(t\) 匹配 \(s\) 次数的最大值。
\(|s|,|t|\le 10^5,|s|\cdot|t|\le 10^7.\)
有了两者长度乘积的限制就不难了,直接dp,设 \(f_{i,j}\) 代表 \(s\) 串前 \(i\) 位,最后 \(j\) 位匹配 \(t\) 的前 \(j\) 位且这是最大的,那么转移的时候枚举 \(?\) 位置放啥即可。
Boyer-Moore
Z-function
定义 最长公共前缀(lcp)
\(\text{lcp}(i,j)\) 为最长的 \(l\) 使得 \(s[i:i+l-1]=s[j:j+l-1]\)。
定义 \(z\) 数组为每个后缀与整个串的 lcp 即 \(z_i=\text{lcp}(1,i)\)。
\(z_1=|s|\),从 \(i=2\) 开始,同时维护两个指针 \(r,l\),分别指向历史最远匹配位置,和那次匹配的初始位置(是不是类似马拉车)。如果 \(i\le r\),根据已知信息可以得到\(z[i] \ge z_{i-l+1}\),可以先令 \(z_{i}=z_{i-l+1}\),然后再暴力匹配。
和马拉车一样,不能超过已知范围,所以还要和 \(r-i+1\) 取个 \(\min\)。
复杂度证明:显然只用分析暴力扩展那一部分,如果当前 \(z_i\) 匹配的部分都是未知的,那么复杂度显然为均摊 \(O(n)\)。如果匹配的是已知部分,由于继承了上一次的匹配,所以是均摊 \(O(r-l)\) 的,而由于每次变化的 \((l,r)\) 是不交的,所以总的复杂度是 \(O(n)\) 的。
void Z(char *s, int *z) {
int len = strlen(s + 1);
for (int i = 2, l = 1, r = 1; i <= len; i++) {
if (i <= r) z[i] = min(r - i + 1, z[i - l + 1]);
while (i + z[i] <= len && s[i + z[i]] == s[z[i] + 1]) z[i]++;
if (i + z[i] - 1 > r) {
l = i;
r = i + z[i] - 1;
}
}
}
如果第一个字符串的前缀 \(s_1[1:i]\)是环的话则必然有一个 \(1\le j<i\),满足 \(s_1[1:j]=s_2[j+1:i],s_1[j+1:i]=s_2[1:j]\)。
所以要做两遍 exkmp,定义 \(p_1\) 为 \(s_1\) 为文本串,\(s_2\) 为模式串的 \(lcp\),\(p_2\) 反过来定义。
现在找到一个位置 \(i\),则 \(s_2[1:{p_1}_{i}]=s_1[i:i+{p_1}_{i}-1]\),现在只要 \({p_2}_{{p_1}_{i}+1}\ge i-1\),即可以够到 \(i\) 即可满足条件。
将答案与 \(i+{p_1}_{i}-1\) 取 \(\max\),最后输出答案。即 \(ans=\max_{p2[p1[i]+1]\ge i-1}(i+p1[i]-1)\)。
XVI PKUSC2023 D1T1
给定 \(S,T\),对于每个 \(i\) 求 \(S_i\) 换为 \(T_i\) 后 \(S\) 的最长 Border。
枚举答案,如果 \(S[:i]\) 和 \(S[|S|-i+1:]\) 有大于等于三位不同,那么不可能成为答案。如果有两位不同,那一定是替换重叠的一位。如果只有一位不同就替换那一位即可。判断有几位不同使用 lcp 即可。
马拉车
马拉车算法是一个用来求最长回文子串的线性算法,由 Manacher 在 1975 年发明。
暴力求解最长回文子串的时间复杂度为 \(O(n^2)\),也可以用字符串哈希加二分做到 \(O(n \times \log{n})\),而 \(Manacher\)算法可以进一步优化到 \(O(n)\)。
因为回文串的长度可以为奇数,也可以为偶数。为了统一,可以在每个字符两边插入一个不再字符集内的字符,这样就不用分情况讨论了。
对于每个位置 \(i\) 求出 \(R_i\) 代表 \(i\) 位置的回文半径。并新增两个变量 \(mx, id\),\(mx\) 代表现在已匹配的回文串右端点最远能到达的位置的下一位,\(id\) 代表\(mx\) 的中心。
- \(mx<i\) 时,有 \(R_{i}\ge 1\)。
- \(mx\ge i\) 时,有 \(R_{i}\ge \min(mx-i,R_{2id-i})\)。
\(R_i\) 的增加和 \(mx\) 的增加是同时进行的,所以算法复杂度是 \(O(n)\)。
XVII LG6216 回文匹配
对于一对字符串 \((s_1,s_2)\),若 \(s_1\) 的长度为奇数的子串 \((l,r)\) 满足 \((l,r)\) 是回文的,那么 \(s_1\) 的“分数”会增加 \(s_2\) 在 \((l,r)\) 中出现的次数。
现在给出一对 \((s_1,s_2)\),请计算出 \(s_1\) 的“分数”。
答案对 \(2 ^ {32}\) 取模。
对于每个位置求是否匹配,然后对于一个回文中心,大概就是统计一个 \(f_l+\dots+f_{r}\),\(f_{l+1}+\dots+f_{r-1}\)。稍微化一下写成发现每个位置的贡献系数是自然数列,拆一下贡献即可。
XIX CF30E Tricky and Clever Password
一个长度为奇数的回文串可以写成 \(a+b+a'\) 的形式(\(a\) 可以为空),其中 \(a'\) 是 \(a\) 的反串。现在将它加密成 \(S\),变成了 \(x+a+y+b+z+a'\) 的形式,给出 \(S\),求最长可能的原串。
马拉车枚举所有奇数长度的回文串,然后观察到 \(a'\) 是一个后缀,直接反过来做 kmp,求出前缀函数。那么对于一个回文串 \(s[l:r]\),求出 \(mx_l\) 代表 \(s[1\dots l-1]\) 这一部分最长匹配长度,然后枚举一下即可。
XX CF17E Palisection
给定一个长度为 \(n\) 的小写字母串。问你有多少对相交的回文子 串(包含也算相交)。
统计不交的部分即可,对于每个位置 \(i\) 求出有多少个回文串 \(\le i\) 结尾以及多少个回文串 \(>i\) 结尾,两者相乘即为答案。
XXI CF1827C Palindrome Partition
称一个字符串是好的,当且仅当它是一个长度为偶数的回文串或由若干长度为偶数的回文串拼接而成。
给定一个长度为 \(n\) 的字符串 \(s\),求有多少 \(s\) 的子串是好的。\(1\le n\le5\times10^5\),\(s\) 仅包含小写字母。
对于一个偶回文串,如果他有一个偶回文后缀,那么他一定可以划分成更多的偶回文串。对于每个位置 \(i\),找出最短的以其为结尾的偶回文子串,转移即可。使用回文自动机可以直接记录,也可以使用 Manacher 是一个区间赋值的过程。其实是一个取 \(\min\) 的操作,可以单调栈维护。复杂度 \(O(n)\)。
THUPC2018 绿绿和串串
基础篇
AC 自动机
USACO15FEB Censoring G
USACO12JAN Video Game G
CF590E
NOI2011 阿狸的打字机
Indie Album
POI2000 病毒
CF1202E You Are Given Some Strings...
COCI2015 Divljak
C1400F x-prime Substrings
观察到 \(x\) 很小,我们跑一遍暴力发现所有 x-prime 数的长度的和最大也不超过 \(5000\)(实测应该是 \(x=19\) 时最大)。那问题就变成了总长度不超过 \(5000\) 的模式串和一个文本串问最少从文本串中删去几个字符可以使得文本串不包含任意一个模式串。
多串匹配问题想到 AC 自动机。这种问题又可以想到动态规划。设 \(dp_{i,j}\) 代表匹配到文本串第 \(i\) 位且当前在AC自动机上的状态 \(j\)。首先下个位置肯定可以删掉,所以 \(dp_{i+1,j}\) 可以为 \(dp_{i,j}+1\)。然后考虑不删下一个字符,则加上下一个字符后一定不能是某个模式串结尾,这可以在 \(fail\) 树上 \(dp\) 求得某个状态是不是某个模式串的结尾。如果不是,则其可以为 \(dp_{i,j}\)。最后的答案就是 \(min(dp_{n,所有状态})\)。
UOJ772 企鹅游戏
LOJ3396 GDSOI2019 novel 加强版
CF710F String Set Queries
CF1801G A task for substrings
后缀数组
Border 理论
回文自动机
后缀自动机
CF1276F
ZJOI2019 语言
提高篇
Lyndon 分解 & Runs
基本子串结构
本文决定重构,并与其他文章合并,更名为【字符串数据结构】
再探pam及其应用
扯淡
为什么要写这篇文章?因为一年前自己非常naive(虽然现在也很naive)的时候写了一篇,然后今年再看的时候发现毫无内容,所以决定再写一篇qwq。
本文其实主要还是2017年论文《回文树及其应用》の学习笔记,补了一些当时因为知识没学而没写的题。
还有就是我教练想让我讲这个内容然后发现之前那个根本拿不出手
LG日报好像只有一篇讲PAM怎么构建的(而且好像还只有基础插入算法),所以本文还想投日报
然而那篇日报貌似对初学者真的挺友好的,所以也推荐去看一下。
正文
1 一些基础记号的定义
我们用 \(\Sigma\) 来表示字符集,\(|\Sigma|\) 来表示字符集大小。
如果没有特殊说明,\(s\) 代表一个字符串,\(|s|\) 是字符串大小,\(s[i]\) 是字符串从一开始的第 \(i\) ,位\(s[l...r]\) 表示 \(s[l]\) 到 \(s[r]\) 这一段子串。
\(s^R\) 代表将 \(s\) 翻转,比如 \(s=akioi,a^R=ioika\)。如果 \(s=s^R\) 则称 \(s\) 是一个回文串。比如 \(s=lxl\)。
一般来讲 \(c\) 代表一个字符,\(sc\) 代表在一个字符串后加一个字符,\(cs,csc\) 同理。
我们定义 \(s\) 的回文后缀为回文且不等于 \(s\) 的后缀,如 \(ababa\) 中 \(aba\) 是回文后缀,但 \(ababa\) 和 \(baba\) 不是。定义最长回文后缀为其最长的回文后缀,比如 \(ababa\) 的最长回文后缀是 \(aba\)。
一般还会用PAM上的一个节点 \(i\) 代表一个回文串,\(f_i\) 是其父亲,\(fail_i\) 是其最长回文后缀所代表的点(为什么要记录下文会提到),\(go_{i,c}\) 为其出边为 \(c\) 的儿子。
2 结构与构造
2.1 结构
PAM 的状态和转移形成一个森林,它有两个根,一个叫奇根(odd),一个叫偶根(even)。树上每个节点除跟外和 \(s\) 的一个回文子串对应。特殊的,odd对应一个长度为 \(-1\) 的串,even对应空串。每个节点的每条儿子边对应一个字符 \(c\),满足 \(i=cf_ic\)。每个节点上记录三个信息 : 最长回文后缀 \(fail\) 指针,该节点回文串长度 \(len\) 和转移边 \(go[]\)。特殊的 \(fail_{odd}=fail_{even}=odd,len_{odd}=-1,len_{even}=0\)。
PAM上包括 \(s\) 的所有本质不同的回文子串,且大小最小。
画出 \(s=abba\) 的 PAM 与 \(fail\) 树。
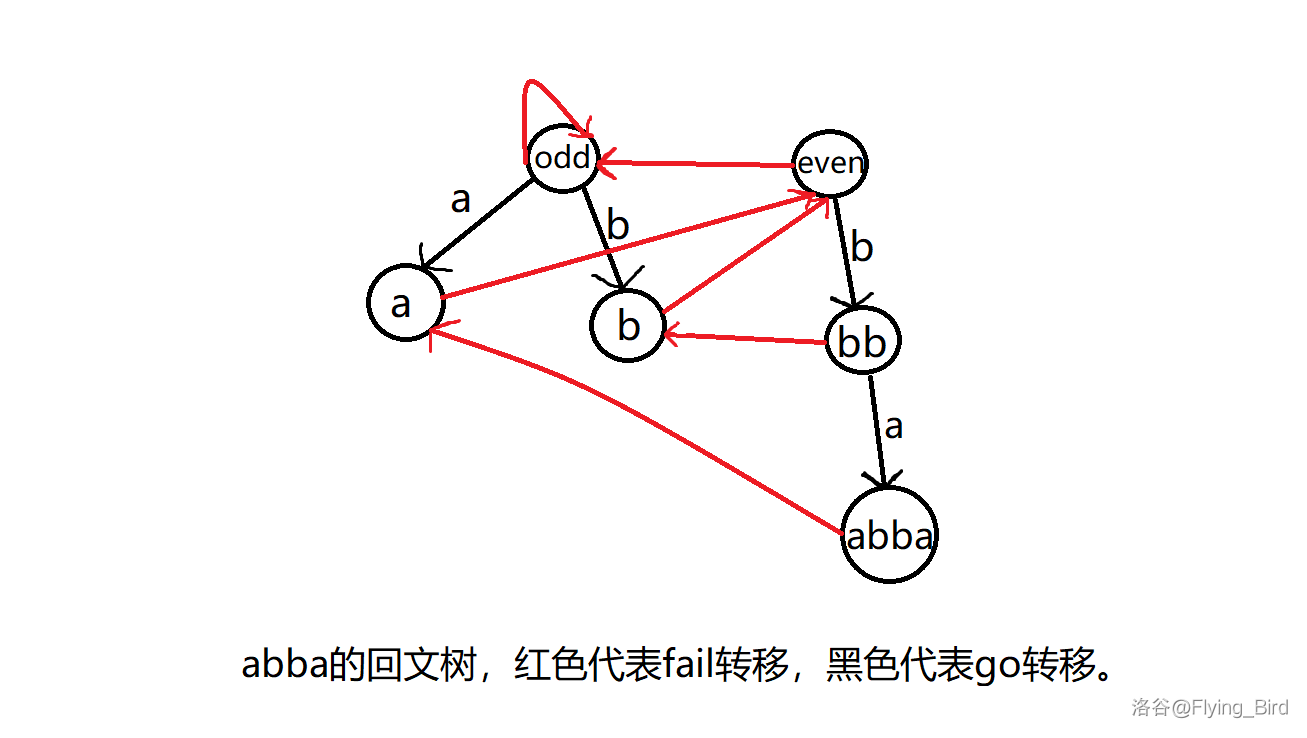
2.2 构造
定理1
\(|s|\) 本质不同的回文子串的个数是 \(O(|s|)\) 的!
证明
考虑在 \(s\) 后加一个字符 \(c\) 形成新的字符串 \(sc\),考虑其回文后缀的开始位置有 \(l_1,l_2...l_k\),从前往后排序。考虑回文串的性质,\(l_i,i>1\) 一定是 \(s[l_1...|sc|]\) 的后缀,又其是回文串,所以其一定在前面作为前缀倒着出现过。又 \(s[l_i...|sc|]\) 也是一个回文串,所以其倒着正着无所谓,那么它就一定在前面出现过。所以每加一个字符只会增加一个回文串。证毕!
容易发现增加一个字符后增加的回文串只会是新串的最长回文后缀。所以我们考虑用增量法构造(所以要记录 \(fail\))。
找到上次加入时的节点(也就是 \(s\) 的最长回文后缀,注意这里可以为 \(s\),记为 \(last\))。如果 \(s[i...|s|]c\) 是回文串,那么 \(s[i]=c\and s[i+1...|s|]\) 也是回文串,记为 \(s\) 的回文后缀。考虑 \(fail\) 的定义,整个 \(fail\) 链上的节点即为所有回文后缀。那么我们直接枚举所有 \(fail\) 链上节点,然后判断 \(s[i]\) 是否等于 \(c\) 即可。
这不是大暴力吗!!!下面证明它的复杂度也是 \(O(|s|)\) 的。
使用势能分析,考虑 \(lst\) 所在节点 \(fail\) 链长度的变化,显然每次最多增加 \(1\) (新建一个节点),由于加入是 \(O(|s|)\) 的,所以在 \(fail\) 链上跳的次数也是 \(O(|s|)\) 的。而空间复杂度显然是 \(O(|\Sigma||s|)\)
我们称这是最基础的算入算法。
2.3 代码实现
int fail[N],len[N],go[N][c];
void build(){
s[0]=-1;
len[1]=-1;len[0]=0;tot=1;lst=0;
fail[1]=fail[0]=1;//这里 1 是 odd 节点,0 是 even 节点
}
/*
* 为什么 0 为偶,1 为奇。因为这时如果最长回文后缀是空串就会直接指向 0,比较方便。
*/
void ins(int n,int c){
int p=lst;
while(s[n-len[p]-1]!=s[n])p=fail[p];
if(!go[p][c]){
//因为没有这个节点,所以还需考虑求出其 fail,复杂度分析同理
int v=++tot,k=fail[p];
len[v]=len[p]+2;
while(s[n-len[k]-1]!=s[n])k=fail[k];
fail[v]=go[k][c];
go[p][c]=v;
}
lst=go[p][c];
}
2.4 经典应用
给定一个字符串 \(s\)。保证每个字符为小写字母。对于 \(s\) 的每个位置,请求出以该位置结尾的回文子串个数。强制在线。\(1\le |s|\le 5\times 10^5\)
容易发现以某个位置为结尾的回文串为 \(s[1...i]\) 的所有回文后缀。也就是不停跳 \(fail\) 上的所有节点。所以答案为 \(fail\) 链的长度(除去两个根)。
给你一个字符串,求其所有回文子串出现次数\(\times\)长度的最大值。\(1 \leq |s| \leq 3 \times 10^5\)。
首先建出 \(s\) 的回文树,然后对于每一个回文子串,记录 \(cnt\) 为它出现的次数。
对于它 \(fail\) 树上的儿子,肯定都是它的子串(后缀),所以他出现了 \(cnt\) 次,它的后缀也会出现 \(cnt\) 次。
因为PAM的 feature 所以我们可以从后往前遍历,假设现在遍历到 \(i\),就使 \(cnt_{fail_i}\) 加上 \(cnt_i\)。
如果要动态维护 \(cnt\) 呢?
3 一些扩展
3.1 前后插入的PAM
写一个数据结构支持前端后端插入,输出回文子串个数以及位置不同的回文子串个数
由于回文串的 feature,所以回文串的最长回文后缀其实和最长回文前缀是一个东西,那么只用一个 \(fail\) 即可。注意需要维护当前串的最长回文前后缀,同时如果当前串是一个回文串,需要同时更新。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int base = 4 * 1e5 + 5;
const int maxn = 1e6 + 5;
char s[maxn], t[maxn];
int len[maxn], fail[maxn], go[maxn][26], tot, lstf, lstb, tot_len, dep[maxn];
ll ans;
void build() {
s[0] = -1; len[tot = 1] = -1; len[0] = 0; fail[1] = fail[0] = 1;
}
void ins_f(int n, int c) {
int p = lstf;
while (s[n + len[p] + 1] != s[n]) p = fail[p];
if (!go[p][c]) {
int v = ++tot, k = fail[p];
len[v] = len[p] + 2;
while (s[n + len[k] + 1] != s[n]) k = fail[k];
fail[v] = go[k][c];
dep[v] = dep[fail[v]] + 1;
go[p][c] = v;
}
lstf = go[p][c];
if (len[lstf] == tot_len) lstb = lstf;
ans += dep[lstf];
}
void ins_b(int n, int c) {
int p = lstb;
while (s[n - len[p] - 1] != s[n]) p = fail[p];
if (!go[p][c]) {
int v = ++tot, k = fail[p];
len[v] = len[p] + 2;
while (s[n - len[k] - 1] != s[n]) k = fail[k];
fail[v] = go[k][c];
dep[v] = dep[fail[v]] + 1;
go[p][c] = v;
}
lstb = go[p][c];
if (len[lstb] == tot_len) lstf = lstb;
ans += dep[lstb];
}
int main() {
scanf("%s", t + 1);
build();
int Len = strlen(t + 1);
for (int i = 1; i <= Len; i++) s[i + base] = t[i];
int l = base + 1, r = base + Len;
for (int i = l; i <= r; i++) tot_len++, ins_b(i, s[i] - 'a');
int Q;
scanf("%d", &Q);
while (Q--) {
int op;
scanf("%d", &op);
if (op == 1) {
scanf("%s", t + 1);
Len = strlen(t + 1);
for (int j = 1; j <= Len; j++) {
tot_len++; s[++r] = t[j];
ins_b(r, s[r] - 'a');
}
} else if (op == 2) {
scanf("%s", t + 1);
Len = strlen(t + 1);
for (int j = 1; j <= Len; j++) {
tot_len++; s[--l] = t[j];
ins_f(l, s[l] - 'a');
}
} else {
printf("%lld\n", ans);
}
}
return 0;
}
3.2 不基于势能分析的插入算法与可持久化
3.2.1 不基于势能分析的插入算法
每次插入一个字符 \(c\) 都要在最长回文后缀的 \(fail\) 上面找到第一个 \(v\) 使得 \(v\) 在 \(s\) 中的前驱是 \(c\)。而 \(v\) 一定在最长回文后缀中,这只与最长回文后缀有关与插入的位置无关。
我们在回文树上的每个节点在多存储一个失配转移数组 \(quick_c\),存储树上一个节点 \(t\) 最长的满足前驱为 \(c\) 的回文后缀。那么在插入时,我们只用判断当前最长回文后缀的前驱是否为 \(c\),若不是则合法的节点就是 \(quick_c\) 的 \(go_c\) 。
我们考虑如何维护 \(quick\)。对于一个节点 \(t\) 和 \(fail_t\) 的 \(quick\) 大部分都是相同的,可以直接复制 \(fail_t\) 的 \(quick\)。若 \(c\) 为 \(t\) 在 \(s\) 中的前驱,则用 \(fail_t\) 更新 \(t\) 的\(quick_c\)。
插入的时空复杂度都是 \(O(|\Sigma|)\)。
int fail[N],len[N],go[N][S],quick[N][S];
void build(){
s[0]=-1;
len[1]=-1;len[0]=0;tot=1;lst=0;
for(int i=0;i<26;i++)quick[0][i]=quick[1][i]=1;
fail[1]=fail[0]=1;//这里 1 是 odd 节点,0 是 even 节点
}
void ins(int n,int c){
int p=quick[lst][c];
if(!go[p][c]){
//因为没有这个节点,所以还需考虑求出其 fail,复杂度分析同理
int v=++tot
len[v]=len[p]+2;
fail[v]=go[quick[p][c]][c];
memcpy(quick[v],quick[fail[v]],sizeof(qucik[fail[v]]));
quick[v][s[n-len[fail[v]]-1]-'a']=fail[v];
go[p][c]=v;
}
lst=go[p][c];
}
3.2.1 后端删除
将 PAM 可持久化,然后删除即相当于查询历史版本。考虑将 \(go,fail,quick\) 都可持久化,对于一个节点的版本,记录其长度,当前版本对应 \(fail\) 的版本。如果用线段树来实现,每个叶子节点代表一个回文树上节点的信息,所以复杂度为 \(O(\log{|s|+|\Sigma|})\)。
然而这玩意似乎并不会有应用,因为出题人也不想搞这么毒瘤
3.3 在 trie 上建 PAM
https://www.codechef.com/problems/TREEPAL
给定一棵以 \(1\) 为根的 \(N\) 个点的树,树上每个点都有一个小写字母。对于树上每个点,求出从根到这个点形成的字符串的最长回文后缀,输出所有点的答案的和。
在 trie 上建 PAM 如果用基础插入算法的话复杂度容易证明是 \(O(\sum dep_{leaf})\)。所以要用不基于势能分析的插入方法。对于此题,我们不妨把整个 trie 的 PAM 建成广义 PAM。我们可以在每个节点都多记录一个值表示当前节点代表的字符串的最长回文后缀在回文树上对应的节点,每次扩展到儿子时只需要直接插入即可。
#include <iostream>
#include <cstdio>
using namespace std;
const int N = 100010;
struct node{
int pre, to;
}edge[N << 1];
int head[N], tt;
struct PAM{
int go[26], quick[26];
int fail;
long long len;
}tr[N];
int tot, cnt[N], Len, top, id[N];
long long ans;
char col[N], s[N];
long long mx[N];
void build() {
s[0] = -1;
tot = 0;
tr[++tot].len = -1;
tr[0].fail = tr[1].fail = 1;
for (int i = 0; i < 26; i++) tr[0].quick[i] = tr[1].quick[i] = 1;
}
int insert(int c, int n, int lst) {
int p = lst;
if (s[n - tr[p].len - 1] != s[n]) p = tr[p].quick[c];
if (!tr[p].go[c]) {
int v = ++tot;
tr[v].len = tr[p].len + 2;
tr[v].fail = tr[tr[p].quick[c]].go[c];
for (int i = 0; i < 26; i++) tr[v].quick[i] = tr[tr[v].fail].quick[i];
tr[v].quick[s[n - tr[tr[v].fail].len] - 'a'] = tr[v].fail;
tr[p].go[c] = v;
}
return tr[p].go[c];
}
void dfs(int x, int fa) {
s[++top] = col[x];
id[x] = insert(s[top] - 'a', top, id[fa]);
mx[x] = max(mx[fa], tr[id[x]].len);
ans += mx[x];
for (int i = head[x]; i; i = edge[i].pre) {
int y = edge[i].to;
if (y == fa) continue;
dfs(y, x);
}
top--;
}
void add(int u, int v) {
edge[++tot] = node{head[u], v};
head[u] = tot;
}
int main() {
cin >> Len;
scanf("%s", col + 1);
for (int i = 1, x, y; i < Len; i++) {
cin >> x >> y;
add(x, y);
add(y, x);
}
build();
dfs(1, 0);
cout << ans;
return 0;
}
3.4 前后插入删除PAM
咕咕咕
4 应用
GDKOI2013大山王国的城市规划(country)
给定一个长度为 \(n\) 的字符串 \(s\),现在要从 \(s\) 中选出尽量多的子串,满足选出的子串都是回文的,并且不存在一个串是另外一个串的子串的情况。(可以部分重叠) \(n \leq 10^5\)。
疑似错题(
首先考虑建出 \(s\) 的 PAM,然后考虑两个串之间如果被包含会有什么样的关系。我们发现如果对于每个点往其父亲和 \(fail\) 都连一条单向边,那么他能到的点就是他所包含的所有回文串。于是我们考虑在建出的 dag 里找最多的点使得其两两不能互相到达。也就是求这个 dag 的最大独立集,根据 dilworth 定理,最大独立集=最长反链=最小链覆盖=传递闭包后的最小路径覆盖。
所以我们先跑传递闭包,然后拆点二分图网络流求最小路径覆盖。
可是这复杂度不是爆炸吗(
如果有更好的方法可以在讨论里提出qwq。
对于一个字符串是 \(s\),考虑一个四元组 \((l,r,L,R)\),当 \(S_{l,r}\) 和 \(S_{L,R}\) 均为回文串时,且满足 $ \leq l \leq r < L \leq R \leq Len$ 时,我们称 \(S_{l,r}\) 和 \(S_{L,R}\) 为一对互不相交的回文串。本题所求,也即为这种四元组的个数。两个四元组相同当且仅当对应的 \(l,r,L,R\) 都相同。
直接考虑枚举 \(r\),然后 \(S_{l,r}\) 个数随便数,后面的部分做一个后缀和即可。
若要x是双倍回文,它的长度必须是4的倍数,而且x、x的前半部分、x的后半部分都要是回文的,你的任务是,对于给定的字符串,计算它的最长双倍回文子串的长度。 \(n \leq 5 \times 10^5\)。
在将这道题时我们需要引入一个新的指针 \(half\),\(half_p\) 指向 \(\leq \frac{len_p}{2}\) 的最长的回文后缀。
我们来看假如求出了这个 \(half\),那么双倍回文子串 \(p\) 即为满足 \(4|len_p\) 且 \(half_p=\frac{len_p}{2}\) 的回文子串。
那这个 \(half\) 怎么求呢?我们可以采用类似 \(fail\) 的求法。
-
若 \(len_p \leq 2\),则其 \(half\) 即为其 \(fail\)。
-
若 \(len_p > 2\),则在 \(f_i\) (\(i\)的父亲)的 \(half\) 的 \(fail\) 链上找,找到第一个 \(l\) ,满足 \(s_{|s|-len_l-1}=c\) (当前插入的字符)且 \(len_l+2 \leq \frac{len_p}{2}\),令 \(half_p=l\) 的 \(go_c\)。
时间复杂度为 \(O(|s|)\),证明类似基础插入算法的证明。
#include <iostream>
#include <cstdio>
using namespace std;
struct PAM{
int go[26], fail, len;
int half;
}pt[500010];
int lst, tot;
int len, ans;
char s[500010];
void build() { s[0] = -1; pt[++tot].len = -1; pt[0].fail = pt[1].fail = 1; }
void insert(int c, int n) {
int p = lst;
while (s[n] != s[n - pt[p].len - 1]) p = pt[p].fail;
if (!pt[p].go[c]) {
int v = ++tot, k = pt[p].fail, l = pt[p].half;
pt[v].len = pt[p].len + 2;
while (s[n] != s[n - pt[k].len - 1]) k = pt[k].fail;
pt[v].fail = pt[k].go[c];
if (pt[v].len > 2) {
while (s[n] != s[n - pt[l].len - 1] || pt[l].len + 2 > pt[v].len / 2) l = pt[l].fail;
pt[v].half = pt[l].go[c];
} else pt[v].half = pt[v].fail;
pt[p].go[c] = v;
lst = pt[p].go[c];
if (pt[lst].len % 4 == 0 && pt[pt[lst].ffail].len == pt[lst].len / 2) ans = max(ans, pt[lst].len);
}
lst = pt[p].go[c];
}
int main() {
scanf("%d%s", &len, s + 1);
build();
for (int i = 1; i <= len; i++) insert(s[i] - 'a', i);
printf("%d", ans);
return 0;
}
给你一个串,让你求出 \(k\) 阶回文子串有多少个。\(k\) 从 \(1\) 到 \(n\)。\(k\) 阶子串的定义是:子串本身是回文串,而且它的左半部分也是回文串。 首先明确: 1、如果一个字串是 \(k\) 阶回文,那他一定还是 \(k-1\) 阶回文。 2、如果一个串是 \(k\) 阶回文,那么这个串需要满足: 1.它本是是回文的。 2.他的左半部分是 \(k-1\) 回文的。
考虑求出所有回文串的最高阶,记为 \(f_i\)。那么当且仅当 \(len_{half_i}=\frac{len_i}{2}\) 时才满足第二个条件,\(f_i=f_{half_i}+1\),否则 \(f_i=1\)。然后做一个后缀和,再用一个堆统计即可。
#include <bits/stdc++.h>
using namespace std;
int go[5005][26], len[5005], fail[5005], dp[5005], cnt[5005], ans[5005], half[5005], lst, tot, Len;
char s[5005];
void build() { s[0] = -1; len[0] = 0; len[1] = -1; fail[0] = fail[1] = 1; tot=1; lst=0;}
void ins(int n, int c) {
int p = lst;
while (s[n - len[p] - 1] != s[n]) p = fail[p];
if (!go[p][c]) {
int v = ++tot, k = fail[p], o = half[p];
len[v] = len[p] + 2;
while (s[n - len[k] - 1] != s[n]) k = fail[k];
fail[v] = go[k][c];
go[p][c] = v;
if (len[v] <= 2) half[v] = fail[v];
else {
while (s[n - len[o] - 1] != s[n] || len[o] + 2 > len[v] / 2) o = fail[o];
half[v] = go[o][c];
}
if (len[half[v]] == len[v] / 2) dp[v] = dp[half[v]] + 1;
else dp[v] = 1;
} lst = go[p][c]; cnt[lst]++;
}
int main() { scanf("%s", s + 1); Len = strlen(s + 1); build();
for (int i = 1; i <= Len; i++) ins(i, s[i] - 'a');
for (int i = tot; i >= 2; i--) cnt[fail[i]] += cnt[i];
for (int i = 2; i <= tot; i++) ans[dp[i]] += cnt[i];
for (int i = Len - 1; i >= 1; i--) ans[i] += ans[i + 1];
for (int i = 1; i <= Len; i++) printf("%d ", ans[i]);
return 0;
}
初始有一个空串,利用下面的操作构造给定串\(S\)。 1、串开头或末尾加一个字符 2、串开头或末尾加一个该串的逆串 求最小化操作数, \(|S| \leq 10^5\)。
花费数量最少那肯定是 \(2\) 操作越多越好。答案一定是某一次 \(2\) 操作之后不停地一操作得来的(可以零次一操作)。
第二种操作后形成的字符串一定是回文串,考虑枚举 \(s\) 的回文子串 \(s[i...j]\),求出构造 \(s[i...j]\) 的代价在加上 \(n-(j-i+1)\) 即可。
建出 \(s\) 的回文树,现在要求构造出每个节点的花费,其实因为二操作后形成的回文串一定是偶回文串,所以我们只用考虑偶回文串。
考虑转移。
在由父节点更新子节点过程中,若直接前后增加一个字符,则花费为 \(2\);但如果在形成父节点前就先在前(或后)增加那个字符,再进行一次操作 \(2\),则花费可以减少 \(1\),也就是额外花费仅为 \(1\)。
所以有 \(dp[SON]=min(dp[SON], dp[FATHER]+1)\)。
我们还得考虑 \(fail\)链上的串。
显然这个值只有可能是不超过当前回文长度一半的最长回文后缀(即 \(half\) 数组,不知道怎么求的戳我),然后先通过操作 \(1\) 到达当前回文串的一半,最后通过操作 \(2\) 直接得到当前回文串。
总时间复杂度是\(O(n)\)。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
using namespace std;
struct node{
int go[4], fail, len;
int half;
}pt[500010];
int lst, tot, t, len, ans, dp[500010];
char s[500010];
int f(char ch) {
if (ch == 'A') return 0;
if (ch == 'C') return 1;
if (ch == 'G') return 2;
if (ch == 'T') return 3;
return 19260817;
}
void build() {
for (int i = 0; i <= tot; i++) for (int j = 0; j < 4; j++) pt[i].go[j] = 0;
tot = lst = 0;
s[0] = -1;
pt[++tot].len = -1;
pt[0].fail = pt[1].fail = 1;
}
void insert(int c, int n) {
int p = lst;
while (s[n] != s[n - pt[p].len - 1]) p = pt[p].fail;
if (!pt[p].go[c]) {
int v = ++tot, k = pt[p].fail;
pt[v].len = pt[p].len + 2;
while (s[n] != s[n - pt[k].len - 1]) k = pt[k].fail;
pt[v].fail = pt[k].go[c];
if (pt[v].len > 2) {
int l = pt[p].half;
while (s[n] != s[n - pt[l].len - 1] || pt[l].len + 2 > pt[v].len / 2) l = pt[l].fail;
pt[v].half = pt[l].go[c];
} else pt[v].half = pt[v].fail;
pt[p].go[c] = v;
dp[v] = pt[v].len;
if (pt[v].len % 2 == 0) {
dp[v] = min(dp[v], dp[p] + 1);
dp[v] = min(dp[v], dp[pt[v].half] + 1 + pt[v].len / 2 - pt[pt[v].half].len);
ans = min(ans, len - pt[v].len + dp[v]);
}
}
lst = pt[p].go[c];
}
int main() {
scanf("%d", &t);
while (t--) {
scanf("%s", s + 1);
len = strlen(s + 1);
ans = len;
build();
dp[0] = 1;
for (int i = 1; i <= len; i++) {
insert(f(s[i]), i);
}
printf("%d\n", ans);
}
return 0;
}
#1113. 秩序魔咒 & #1105. 快乐的 JYY[JSOI 2013]
双串最长公共回文子串。
求两个字符串的相等回文子串对子数。
建出两棵 PAM 然后直接在上面同时 dfs 即可。
//秩序魔咒
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
struct node{
int go[26], len, fail;
}pt[2][500010];//0:A ; 1:B
int Len[2], tot[2], lst[2], ans_len, ans_num;//长度 个数
char s[2][500010];
void build(int id) {
s[id][0] = -1;
pt[id][++tot[id]].len = -1;
pt[id][0].fail = pt[id][1].fail = 1;
}
void insert(int id, int c, int n) {
int p = lst[id];
while (s[id][n - pt[id][p].len - 1] != s[id][n]) p = pt[id][p].fail;
if (!pt[id][p].go[c]) {
int v = ++tot[id], k = pt[id][p].fail;
pt[id][v].len = pt[id][p].len + 2;
while (s[id][n - pt[id][k].len - 1] != s[id][n]) k = pt[id][k].fail;
pt[id][v].fail = pt[id][k].go[c];
pt[id][p].go[c] = v;
}
lst[id] = pt[id][p].go[c];
}
void init(int id) { for (int i = 1; i <= Len[id]; i++) {insert(id, s[id][i] - 'a', i); }
void solve(int x, int y) {
//第一棵树中的编号,第二棵树中的编号
if (pt[0][x].len > ans_len) ans_len = pt[0][x].len, ans_num = 1;
else if (pt[0][x].len == ans_len) ans_num++;
for (int i = 0; i < 26; i++) if (pt[0][x].go[i] && pt[1][y].go[i]) solve(pt[0][x].go[i], pt[1][y].go[i]);
}
int main() {
scanf("%d%d%s%s", &Len[0], &Len[1], s[0] + 1, s[1] + 1);
build(0); build(1);
init(0); init(1);
solve(1, 1); solve(0, 0);
printf("%d %d\n", ans_lne, ans_num);
return 0;
}
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
struct node{
int go[26], len, fail;
ll cnt;
}pt[2][50010];//0:A ; 1:B
int Len[2], tot[2], lst[2];
char s[2][50010];
ll ans;
void build(int id) {
s[id][0] = -1;
pt[id][++tot[id]].len = -1;
pt[id][0].fail = pt[id][1].fail = 1;
}
void insert(int id, int c, int n) {
int p = lst[id];
while (s[id][n - pt[id][p].len - 1] != s[id][n]) p = pt[id][p].fail;
if (!pt[id][p].go[c]) {
int v = ++tot[id], k = pt[id][p].fail;
pt[id][v].len = pt[id][p].len + 2;
while (s[id][n - pt[id][k].len - 1] != s[id][n]) k = pt[id][k].fail;
pt[id][v].fail = pt[id][k].go[c];
pt[id][p].go[c] = v;
}
pt[id][pt[id][p].go[c]].cnt++;
lst[id] = pt[id][p].go[c];
}
void init(int id) {
for (int i = 1; i <= Len[id]; i++) insert(id, s[id][i] - 'A', i);
for (int i = tot[id]; i > 1; i--) pt[id][pt[id][i].fail].cnt += pt[id][i].cnt;
}
void solve(int x, int y) {
for (int i = 0; i < 26; i++) {
if (pt[0][x].go[i] && pt[1][y].go[i]) {
ans += pt[0][pt[0][x].go[i]].cnt * pt[1][pt[1][y].go[i]].cnt;
solve(pt[0][x].go[i], pt[1][y].go[i]);
}
}
}
int main() {
scanf("%s%s", s[0] + 1, s[1] + 1);
Len[0] = strlen(s[0] + 1);
Len[1] = strlen(s[1] + 1);
build(0); build(1);
init(0); init(1);
solve(1, 1); solve(0, 0);
printf("%lld\n", ans);
return 0;
}
区间本质不同回文串个数,强制在线,\(n\le 10^5\)。
- 算法1 大力分块
不想讲了,就是一暴力。
-
算法2 利用回文 border 的性质
-
算法3 套用 LCT???做到 \(O(n\log{n})\)???
求 \(\sum_{1\le x\le y\le |s|}LCP(x,y)\),其中 \(LCP(x,y)\) 是前缀的最长公共回文后缀,动态加入字符,查询,强制在线。操作数 \(\le 10^5\)。
题目中的LCP其实就是fail树上的LCA,那么就好做了,考虑加入字符时的贡献。从其每个祖先入手,再转换为边的贡献,变量只有子树大小,用LCT维护即可。
5 回文串border
我不会,快去问 xwp 或 mhy。
根据字符串border性质,border构成 log 段等差数列。应用在回文串上即为回文后缀。
考虑求出每段等差数列的公差和首项
int ins(int c, int n) {
int p = lst;
while (s[n - len[p] - 1] != s[n]) p = fail[p];
if (!son[p][c]) {
int v = ++tot, k = fail[p];
len[v] = len[p] + 2;
while (s[n - len[k] - 1] != s[n]) k = fail[k];
fail[v] = son[k][c];
d[v] = len[v] - len[fail[v]];
top[v] = d[v] == d[fail[v]] ? top[fail[v]] : fail[v];
son[p][c] = v;
}
return lst = son[p][c];
}
https://codeforces.com/problemset/problem/906/E
3300
给定字符串 \(s,t\),可以翻转 \(t\) 的若干不相交的区间,使得 \(t=s\),求最少翻转几个区间?\(|s|,|t|\le 5\times 10^5\)
翻转区间相等看起来想一个回文串,我们重新构造,把 \(t\) 插入 \(s\),构造一个 \(s[1]t[1]s[2]t[2]...s[n]t[n]\) 这样的字符串。然后我们发现题目要求即为最小的偶回文划分。当然相同的部分会形成若干长度为 \(2\) 的回文串,这时我们需要特殊处理。
具体考虑 dp,设 \(f_i\) 代表前 \(i\) 个位置的最小花费。显然有 \(f_i=\min_{s[j+1...i] is palindrome} f_j + 1\),不过还有第二种转移,在 \(s[i]=s[i-1]\) 时可以不用任何花费从 \(f_{i-2]\) 转移过来。然后我们发现前者可以利用回文串 border 的性质优化,就 \(O(nlog{n})\) 了。
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e6 + 5;
int mark[maxn], pre[maxn], g[maxn], f[maxn], top[maxn], d[maxn], len[maxn], fail[maxn], go[maxn][26], tot, lst;
char t[maxn], tt[maxn], s[maxn];
void build() { s[0] = -1; len[tot = 1] = -1; len[0] = 0; fail[1] = fail[0] = 1; }
int ins(int n, int c) {
int p = lst;
while (s[n - len[p] - 1] != s[n]) p = fail[p];
if (!go[p][c]) {
int v = ++tot, k = fail[p];
len[v] = len[p] + 2;
while (s[n - len[k] - 1] != s[n]) k = fail[k];
fail[v] = go[k][c];
d[v] = len[v] - len[fail[v]];
top[v] = d[v] == d[fail[v]] ? top[fail[v]] : fail[v];
go[p][c] = v;
}
return lst = go[p][c];
}
int main() {
memset(f, 0x3f, sizeof(f));
f[0] = 0;
scanf("%s%s", t + 1, tt + 1);
int Len = strlen(t + 1);
for (int i = 1; i <= Len; i++) s[2 * i - 1] = t[i], s[2 * i] = tt[i];
Len <<= 1; build();
for (int i = 1; i <= Len; i++) {
ins(i, s[i] - 'a');
for (int j = lst; j > 1; j = top[j]) {
g[j] = i - len[top[j]] - d[j];
if (d[j] == d[fail[j]]) {
if (f[g[j]] > f[g[fail[j]]]) {
g[j] = g[fail[j]];
}
}
if (i % 2 == 0) {
if (f[g[j]] + 1 < f[i]) {
f[i] = f[g[j]] + 1;
pre[i] = g[j];
mark[i] = 1;
}
}
}
if (i % 2 == 0) {
if (s[i] == s[i - 1] && f[i - 2] < f[i]) {
f[i] = f[i - 2];
pre[i] = i - 2;
mark[i] = 0;
}
}
}
if (f[Len] >= 0x3f3f3f3f) {
puts("-1");
return 0;
}
printf("%d\n", f[Len]);
for (int i = Len; i; i = pre[i]) {
if (mark[i])
printf("%d %d\n", pre[i] / 2 + 1, i / 2);
}
return 0;
}
做题的收获?知道了翻转相等和回文串的转化关系;明白了为什么这么转移 \(g\) 是对的。
标签:pt,int,len,fail,go,字符串,回文 From: https://www.cnblogs.com/zcr-blog/p/17497223.html