题目描述:
在一个二维平面上,有一个镜面通道,由镜面 \(AC, BD\) 组成,\(AC, BD\) 长度相等,且都平行于 \(x\) 轴,\(B\) 位于 \((0,0)\)。
通道中有 \(n\) 个外表面为镜面的光学元件,光学元件 \(\alpha\) 为圆形,光学元件 \(\beta\) 为矩形(这些元件可以与其他元件和通道有交集,具体看下图)。光线可以在 \(AB\) 上任一点以任意角度射入通道,光线不会发生削弱。当出现元件与元件,元件和通道刚好接触的情况视为光线无法透过(比如两圆相切)。
现在给出通道中所有元件的信息(\(\alpha\) 元件包括圆心坐标和半径 \(x_i, y_i, r_i\),\(\beta\) 元件包括左下角和右上角坐标 \(x_1, y_1, x_2, y_2\))
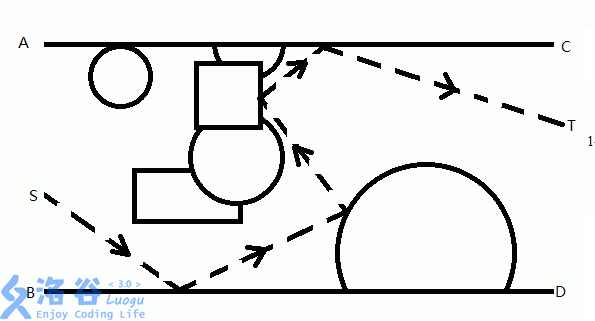
如上图,\(S\) 到 \(T\) 便是一条合法线路。

当然,显然存在光线无法透过的情况,现在交给你一个艰巨的任务,请求出至少拿走多少个光学元件后,存在一条光线线路可以从 \(CD\) 射出。
下面举例说明:
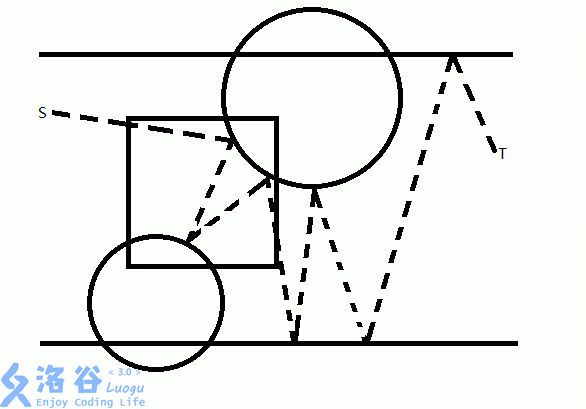
现在假设,取走中间那个矩形,那么就可以构造出一条穿过通道的光路,如图中的 \(S\) 到 \(T\)。
\(x\leq 10^5\),\(y\leq 1000\),\(n\leq 300\)。
题目分析:
有一个显然的结论:如果我们任意方向走可以走通,那么就有解,也就是只要镜面中间有缝可以过去就有解。
那么就考虑怎么判断,显然需要转化为图论模型,考虑对于每一个元件建一个点,对于有交的元件之间连边。
因为会发现这个有缝就可以理解为上下不连通也就是最小割模型,所以我们只需要将 AC 作为源点,BD 作为汇点跑一个最小割就好了
需要注意的就是:我们的操作为删点而非删边,所以我们应该将每一个点拆点,在拆成的两个点之间连流量为 \(1\) 的边,此时删边一定不比删点优,所以最小割都为删点。
代码:
(直接复制的题解的,因为计算几何部分太难写了)
点击查看代码
#include<bits/stdc++.h>
using namespace std;const double eps=1e-7;const int INF=1e9;
struct rnd{double x,y,r;int id;}a[1205];
struct squ{double x1,y1,x2,y2;int id;}b[1205];
struct edge{int to,w,nxt;}e[2000005];
double Cx,Cy;int n,et,s,t,head[1205],d[1205],cr[1205],ac,bc;
inline char chk(squ a,double x,double y) {return a.x1-eps<=x&&x<=a.x2+eps&&a.y1-eps<=y&&y<=a.y2+eps;}
inline char CHK(squ a,double y,double x1,double x2) {return (a.y1-eps<=y&&y<=a.y2+eps)||chk(a,x1,y)||chk(a,x2,y);}
inline char chk1(rnd a,double x,double y1,double y2)
{
if((a.x-x)*(a.x-x)+(a.y-y1)*(a.y-y1)<=a.r*a.r+eps) return 1;
if((a.x-x)*(a.x-x)+(a.y-y2)*(a.y-y2)<=a.r*a.r+eps) return 1;
if(!(a.x-x<=a.r+eps&&a.x-x>=a.r-eps)) return 0;
double dy=sqrt(a.r*a.r-(a.x-x)*(a.x-x)),Y1=a.y-dy,Y2=a.y+dy;
return (y1-eps<=Y1&&Y1<=y2+eps)||(y1-eps<=Y2&&Y2<=y2+eps);
}
inline char chk2(rnd a,double y,double x1,double x2)
{
if((a.x-x1)*(a.x-x1)+(a.y-y)*(a.y-y)<=a.r*a.r+eps) return 1;
if((a.x-x2)*(a.x-x2)+(a.y-y)*(a.y-y)<=a.r*a.r+eps) return 1;
if(!(a.y-y<=a.r+eps&&a.y-y>=-a.r-eps)) return 0;
double dx=sqrt(a.r*a.r-(a.y-y)*(a.y-y)),X1=a.x-dx,X2=a.x+dx;
return (x1-eps<=X1&&X1<=x2+eps)||(x1-eps<=X2&&X2<=x2+eps);
}
inline char operator+(rnd a,rnd b) {return (a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y)<=(a.r+b.r+eps)*(a.r+b.r+eps);}
inline char operator+(squ a,squ b) {return chk(a,b.x1,b.y1)||chk(a,b.x1,b.y2)||chk(a,b.x2,b.y1)||chk(a,b.x2,b.y2);}
inline char operator+(squ a,rnd b)
{
if((a.x1-b.x)*(a.x1-b.x)+(a.y1-b.y)*(a.y1-b.y)<=b.r*b.r+eps) return 1;
if((a.x2-b.x)*(a.x2-b.x)+(a.y1-b.y)*(a.y1-b.y)<=b.r*b.r+eps) return 1;
if((a.x1-b.x)*(a.x1-b.x)+(a.y2-b.y)*(a.y2-b.y)<=b.r*b.r+eps) return 1;
if((a.x2-b.x)*(a.x2-b.x)+(a.y2-b.y)*(a.y2-b.y)<=b.r*b.r+eps) return 1;
if(chk(a,b.x,b.y)) return 1;
if(chk1(b,a.x1,a.y1,a.y2)||chk1(b,a.x2,a.y2,a.y2)||chk2(b,a.y1,a.x1,a.x2)||chk2(b,a.y2,a.x1,a.x2)) return 1;
return 0;
}
inline void ADDE(int x,int y,int w) {e[++et]=(edge){y,w,head[x]},head[x]=et;}
inline void adde(int x,int y,int w) {ADDE(x,y,w),ADDE(y,x,0);}
inline char bfs(int s,int t)
{
queue<int>q;q.push(s),memset(d,0,sizeof(d)),d[s]=1;
while(!q.empty())
{
int x=q.front();q.pop();
for(int i=head[x];i;i=e[i].nxt) if(e[i].w&&!d[e[i].to]) d[e[i].to]=d[x]+1,q.push(e[i].to);
}
return !!d[t];
}
#define rev(x) ((((x)&1)?1:-1)+(x))
inline int dfs(int x,int t,int lim=INF)
{
int f=lim;if(x==t) return lim;
for(int i=cr[x];i;cr[x]=i=e[i].nxt) if(d[e[i].to]==d[x]+1&&e[i].w)
{
int g=dfs(e[i].to,t,min(f,e[i].w));f-=g;
e[i].w-=g,e[rev(i)].w+=g;if(!f) break;
}
return lim-f;
}
inline int dinic(int s,int t) {int r=0;while(bfs(s,t)) memcpy(cr,head,sizeof(cr)),r+=dfs(s,t);return r;}
int main()
{
scanf("%lf%lf%d",&Cx,&Cy,&n),et=0,memset(head,0,sizeof(head)),s=n<<1|1,t=s+1;
for(int i=1,fg;i<=n;i++)
{
scanf("%d",&fg);if(fg^2) ++ac,scanf("%lf%lf%lf",&a[ac].x,&a[ac].y,&a[ac].r),a[ac].id=i;
else bc++,scanf("%lf%lf%lf%lf",&b[bc].x1,&b[bc].y1,&b[bc].x2,&b[bc].y2),b[bc].id=i;
}
for(int i=1;i<=n;i++) adde(i,i+n,1);
for(int i=1;i<=ac;i++) if(chk2(a[i],0,0,Cx)) adde(s,a[i].id,1);
for(int i=1;i<=bc;i++) if(CHK(b[i],0,0,Cx)) adde(s,b[i].id,1);
for(int i=1;i<=ac;i++) if(chk2(a[i],Cy,0,Cx)) adde(a[i].id+n,t,1);
for(int i=1;i<=bc;i++) if(CHK(b[i],Cy,0,Cx)) adde(b[i].id+n,t,1);
for(int i=1;i<=ac;i++) for(int j=1;j<=ac;j++) if(i!=j&&a[i]+a[j]) adde(a[i].id+n,a[j].id,1);
for(int i=1;i<=bc;i++) for(int j=1;j<=ac;j++) if(i!=j&&b[i]+a[j]) adde(b[i].id+n,a[j].id,1);
for(int i=1;i<=ac;i++) for(int j=1;j<=bc;j++) if(i!=j&&b[j]+a[i]) adde(a[i].id+n,b[j].id,1);
for(int i=1;i<=bc;i++) for(int j=1;j<=bc;j++) if(i!=j&&(b[i]+b[j]||b[j]+b[i])) adde(b[i].id+n,b[j].id,1);
return printf("%d\n",dinic(s,t)),0;
}