首页 > 其他分享 >不要用define，会变得不幸

不要用define，会变得不幸

时间：2023-06-10 10:11:25浏览次数：43  
标签：rt ch int 不幸 fx id query 变得 define

[BJOI2014]大融合

题目描述

小强要在 \(N\) 个孤立的星球上建立起一套通信系统。这套通信系统就是连接 \(N\) 个点的一个树。

这个树的边是一条一条添加上去的。

在某个时刻，一条边的负载就是它所在的当前能够联通的树上路过它的简单路径的数量。

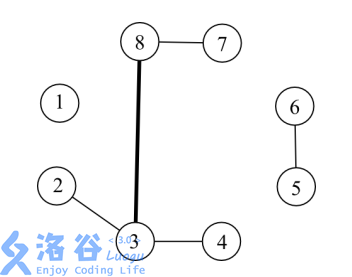
例如，在上图中，现在一共有了 \(5\) 条边。其中，\((3,8)\) 这条边的负载是 \(6\)，因为有六条简单路径 \(2-3-8\),\(2-3-8-7\),\(3-8,3-8-7\),\(4-3-8\),\(4-3-8-7\) 路过了 \((3,8)\)。

现在，你的任务就是随着边的添加，动态的回答小强对于某些边的负载的询问。

输入格式

第一行包含两个整数 \(N, Q\),表示星球的数量和操作的数量。星球从 \(1\) 开始编号。

接下来的 \(Q\) 行，每行是如下两种格式之一：

  • A x y 表示在 \(x\) 和 \(y\) 之间连一条边。保证之前 \(x\) 和 \(y\) 是不联通的。
  • Q x y表示询问 \((x,y)\) 这条边上的负载。保证 \(x\) 和 \(y\) 之间有一条边。

输出格式

对每个查询操作，输出被查询的边的负载。

样例 #1

样例输入 #1

8 6
A 2 3
A 3 4
A 3 8
A 8 7
A 6 5
Q 3 8

样例输出 #1

6

提示

对于所有数据，\(1≤N,Q≤10^5\)

思路不是很难，而且题解一大堆，就不写了。
在这里给我的朋友打个广告：传送门
今天主要是来说说我的代码出现的抽象问题。

第一版

#include<bits/stdc++.h>
using namespace std;
#define il inline
#define lol long long
#define rg register
const int Megellan=3e6;
const int DWDB_221E=1e5+50;
#define Croll(i,l,r) for(rg int i=l;i<=r;i++)
//////////
#define lid tr[id].ls
#define rid tr[id].rs
#define fx find(x)
#define fy find(y)
//////////
struct star{int v,nt;};
star o[DWDB_221E];
void add(int,int);
int head[DWDB_221E];
int tot;//add
//////////
struct line{int ls,rs;int num;};
line tr[Megellan];
int rt[Megellan];
void pushup(int);
int merge(int,int,int,int);
void update(int &,int,int,int);
lol query(int,int,int,int,int);
int cnt;//update
//////////
void dfs(int,int);
int siz[DWDB_221E];
int g[DWDB_221E];
int in[DWDB_221E];
int m;//in
//////////
int fa[DWDB_221E];
int find(int x){return x==fa[x]?x:fa[x]=find(fa[x]);}
//////////
struct offline{char op;int x,y;};
offline p[DWDB_221E];
int n,q;il int read();
//////////
int main()
{
    n=read();q=read();
    Croll(i,1,q)
    {
        char opt;cin>>opt;p[i].op=opt;
        p[i].x=read();p[i].y=read();
        if(opt=='A')
        {add(p[i].x,p[i].y);add(p[i].y,p[i].x);}
    }
    Croll(i,1,n)
        if(!in[i])
            dfs(i,0);
    Croll(i,1,n)
    {update(rt[i],1,m,in[i]);fa[i]=i;}
    Croll(i,1,q)
    {
        char opt=p[i].op;
        int x=p[i].x,y=p[i].y;
        if(opt=='A')
        {
            fa[fy]=fx;
            rt[fx]=merge(rt[fx],rt[fy],1,m);
        }
        else
        {
            if(g[x]==y)swap(x,y);
            lol ans1=query(rt[fx],1,m,in[y],in[y]+siz[y]-1);
            lol ans2=query(rt[fx],1,m,1,in[y]-1)
                    +query(rt[fx],1,m,in[y]+siz[y],n);
            lol ans=ans1*ans2;
            cout<<ans1<<"     "<<ans2<<endl;
            cout<<ans<<endl;
        }
    }
}
void dfs(int x,int father)
{
    siz[x]=1;g[x]=father;
    in[x]=++m;
    for(int i=head[x];i;i=o[i].nt)
    {
        int y=o[i].v;
        if(y==father)continue;
        dfs(y,x);siz[x]+=siz[y];
    }
}
void update(int &id,int l,int r,int x)
{
    if(!id)id=++cnt;
    if(l==r){tr[id].num=1;return;}
    int mid=(l+r)>>1;
    if(x<=mid)update(lid,l,mid,x);
    else update(rid,mid+1,r,x);
    pushup(id);
}
int merge(int id,int b,int l,int r)
{
   if(!id || !b)return id+b;
   if(l==r){tr[id].num+=tr[b].num;return id;}
   int mid=(l+r)>>1;
   lid=merge(lid,tr[b].ls,l,mid);
   rid=merge(rid,tr[b].rs,mid+1,r);
   pushup(id);return id;
}
lol query(int id,int l,int r,int x,int y)
{
    if(!id || y<l || x>r)  return 0;
    if(x<=l && r<=y)return tr[id].num;
    int mid=(l+r)>>1;
    return query(lid,l,mid,x,y)+query(rid,mid+1,r,x,y);
}
void pushup(int id)
{tr[id].num=tr[lid].num+tr[rid].num;}
il int read()
{
    int x=0,w=1;
    char ch;ch=getchar();
    while(ch<'0'||ch>'9') {if(ch=='-') w=-1;ch=getchar();}
    while(ch>='0'&&ch<='9') {x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
    return x*w;
}
il void add(int u,int v)
{
    tot++;
    o[tot].v=v;
    o[tot].nt=head[u];
    head[u]=tot;
}

第二份：

#include<bits/stdc++.h>
using namespace std;
#define il inline
#define lol long long
#define rg register
const int Megellan=3e7;
const int DWDB_221E=1e6+50;
#define Croll(i,l,r) for(rg int i=l;i<=r;i++)
//////////
#define lid tr[id].ls
#define rid tr[id].rs
//////////
struct star{int v,nt;};
star o[DWDB_221E];
void add(int,int);
int head[DWDB_221E];
int tot;//add
//////////
struct line{int ls,rs;int num;};
line tr[Megellan];
int rt[Megellan];
void pushup(int);
int merge(int,int,int,int);
void update(int &,int,int,int);
int query(int,int,int,int,int);
int cnt;//update
//////////
void dfs(int,int);
int siz[DWDB_221E];
int g[DWDB_221E];
int in[DWDB_221E];
int m;//in
//////////
int fa[DWDB_221E];
int find(int x){return x==fa[x]?x:fa[x]=find(fa[x]);}
//////////
struct offline{char op;int x,y;};
offline p[DWDB_221E];
int n,q;il int read();
//////////
int main()
{
    n=read();q=read();
    Croll(i,1,q)
    {
        char opt;cin>>opt;p[i].op=opt;
        p[i].x=read();p[i].y=read();
        if(opt=='A')
        {add(p[i].x,p[i].y);add(p[i].y,p[i].x);}
    }
    Croll(i,1,n)
        if(!in[i])
            dfs(i,0);
    Croll(i,1,n)
    {update(rt[i],1,m,in[i]);fa[i]=i;}
    Croll(i,1,q)
    {
        char opt=p[i].op;
        int x=p[i].x,y=p[i].y;
        int fx=find(x),fy=find(y);
        if(opt=='A')
        {
            fa[fy]=fx;
            rt[fx]=merge(rt[fx],rt[fy],1,m);
        }
        else
        {
            if(g[x]==y)swap(x,y);
            lol ans1=query(rt[fx],1,m,in[y],in[y]+siz[y]-1);
            lol ans2=query(rt[fx],1,m,1,in[y]-1)
                    +query(rt[fx],1,m,in[y]+siz[y],n);
            lol ans=ans1*ans2;
            //cout<<ans1<<"     "<<ans2<<endl;
            cout<<ans<<endl;
        }
    }
}
void dfs(int x,int father)
{
    siz[x]=1;g[x]=father;
    in[x]=++m;
    for(int i=head[x];i;i=o[i].nt)
    {
        int y=o[i].v;
        if(y==father)continue;
        dfs(y,x);siz[x]+=siz[y];
    }
}
void update(int &id,int l,int r,int x)
{
    if(!id)id=++cnt;
    if(l==r){tr[id].num=1;return;}
    int mid=(l+r)>>1;
    if(x<=mid)update(lid,l,mid,x);
    else update(rid,mid+1,r,x);
    pushup(id);
}
int merge(int id,int b,int l,int r)
{
   if(!id || !b)return id+b;
   if(l==r){tr[id].num+=tr[b].num;return id;}
   int mid=(l+r)>>1;
   lid=merge(lid,tr[b].ls,l,mid);
   rid=merge(rid,tr[b].rs,mid+1,r);
   pushup(id);return id;
}
int query(int id,int l,int r,int x,int y)
{
    if(!id || y<l || x>r)  return 0;
    if(x<=l && r<=y)return tr[id].num;
    int mid=(l+r)>>1;
    return query(lid,l,mid,x,y)+query(rid,mid+1,r,x,y);
}
void pushup(int id)
{tr[id].num=tr[lid].num+tr[rid].num;}
il int read()
{
    int x=0,w=1;
    char ch;ch=getchar();
    while(ch<'0'||ch>'9') {if(ch=='-') w=-1;ch=getchar();}
    while(ch>='0'&&ch<='9') {x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
    return x*w;
}
il void add(int u,int v)
{
    tot++;
    o[tot].v=v;
    o[tot].nt=head[u];
    head[u]=tot;
}

不能说一模一样，只能说完全一致。
但是第一份是错的，如果输出ans1和ans2的话，
ans1和ans2中的一个会在一个测试点里全爆零

仔细看的话，第一份在找x和y的fa[]时用了define，但第二份是直接int了一个变量。
有区别吗？有，而且很大。

简单来说，第一版在找fa[]时，是用一次找一次，也就是找现在的版本。
但是在opt== 'A'里，改变了fa[]的值，如果此后，再用fx（也就是merge里）就是改变之后的结果了。
那显然就是错的了，因为我们找的是原本的fa[]。

当然，也有人会说，既然改变fa[]会影响merge（），那就先merge（）再改变fa[]不就行了？

。。。
你说得对，但是（）

经测试，改变merge()和fa[]的顺序后，结果是正确的.可喜可贺，可喜可贺。

差不多结束了，本来就是篇碎碎念，没打算写多长。简单总结一下：
如果define里用的是一个函数，首先要注意的是，它是每用一次运行一次，所以可能会卡时间。
这道题可能对这点体现的不是很明显，因为并查集压缩路径了，每次询问是O（1）的；
即便不考虑时间复杂度，也要考虑作者在上文中出现的问题，因为它是现运行现找，返回的是现在的结果。如果你的代码里既有修改也有使用，要仔细考虑顺序。

最后感谢@admadm,@Flandreqwq，@midsu @Sonnety几位大佬的测试和讲解！万分感谢！！！

over.

标签：rt,ch,int,不幸,fx,id,query,变得,define
From： https://www.cnblogs.com/Cayde-6/p/17470832.html

相关文章

  • cv2 undefined symbol: g_date_copy (or qt.qpa.plugin: Could not load..)解决
    cv2undefinedsymbol:g_date_copyorqt.qpa.plugin:Couldnotload问题背景：这次就是想用Qt5在Ubuntu上做一个GUI，结果一运行就报这个：QObject::moveToThread:Currentthread(0x7fc0f7435300)isnottheobject’sthread(0x7fc0f9f02cc0).Cannotmovetotargetthread(0x7......
  • rosetta mpi运行错误，libcore.2.so undefined s 的
    重装的ubuntu2004，分别安装了openmpi4.1.1及openmpi1.6.5后编译mpi版本rosetta，运行rosetta_script.mpi.linuxgccrelease均出现libcore.2.so的报错，猜测是mpi版本问题或者是手动安装的mpi编译时出现的问题。后面使用apt重装了ubuntu自带的openmpi4.0.3及lib库，重新编译rosetta，发现能......
  • 报错：[Vue warn]: Error in render: "TypeError: Cannot read properties of undefined
    1.错误详情2.错误分析百度此错误发现，很多人可能忘记在main.js中引入store.js并挂载在vue实例上，或者state单词写错了我审查了很多遍代码，依然报错，读取不到state中的数据，后来想到可能是版本的问题此项目是vue2，要使用vuex3才能正常运行，我安装的时候没有指定版本，直接装的是最新的v......
  • VUE Error: Cannot call .tap() on a plugin that has not yet been defined. Call pl
    在对一个vue项目执行过“npmauditfix--force”命令之后，就出现了如下错误： ERROR Error:Cannotcall.tap()onapluginthathasnotyetbeendefined.Callplugin('preload').use(<Plugin>)first.有2个解决方法：方法一：删除之前的源码模块，重新下载后执行“npminstall......
  • JS通过 navigator.clipboard.writeText(textToCopy) 实现文本复制，navigator.clipboard
    问题描述代码：letgeometries=qChart.value.filter((e)=>e.geometry).map((e)=>e?.geometry);navigator.clipboard.writeText(JSON.stringify(geometries)).then(()=>{proxy.$modal.msgSuccess("已复制");}).catch(()=>{......
  • python打包后，执行报错：NameError: name ‘exit‘ is not defined
    try:file_name=os.path.basename(src)file_size=os.stat(src).st_sizeexceptException:print("源文件不存在:",src)exit()在ide使用中没有问题，但是封装成应用程序时就出现问题： NameError:name'exit'isnotdef......
  • Jmeter函数助手39-isPropDefined
    isPropDefined函数用于判断属性是否存在。变量的名称：填入属性名。如果属性名存在返回true，如果不存在返回false 1、jmeter的属性查看路径：测试计划右键“添加”->非测试元件->属性显示2、如果属性存在则返回true。${__isPropDefined(START.YMD)}3、如果属性不存在则返......
  • Jmeter函数助手38-isVarDefined
    isVarDefined函数用于判断变量是否存在。变量的名称：填入变量名称。如果变量存在返回true，如果不存在返回false 1、先一些定义变量${__isVarDefined(now)}，now变量是不存在的故函数结果会返回false${__isVarDefined(tody)} ，today变量是存在的故函数结果会返回true ......
  • [linux]undefined reference to `__gxx_personality_v0'
    linux程序 #include#include#includeintcount=0;voidctrl_c_count(int);intmain(void){intc;void(*old_handler)(int);old_handler=signal(SIGINT,ctrl_c_count);while((c=getchar()!=''));printf("Ctrl_Ccount=%d",count);......
  • The valid characters are defined in RFC 7230 and RFC 3986问题
    最近在ssm实践项目中遇到了ThevalidcharactersaredefinedinRFC7230andRFC3986这个问题，折腾了两天时间终于搞定了，记录一下心得。1、首先贴出报错日志：09-Apr-201914:55:11.427信息[http-nio-8089-exec-8]org.apache.coyote.http11.Http11Processor.serviceErrorpars......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99