题意:构造一张网格图,其中有些边不能跨过,使 \((1,1)\) 到 \((n,m)\) 恰有 \(k\) 边。
\(k \leq 10^{18}\)
考虑从 \(k\) 构造出 \(2k\) 或 \(2k+1\),我们就能用二进制拆分了!
让一圈 \(1\) 围着我们递推的地方,这样当我们需要 \(1\) 时就能随手开一道门让 \(1\) 流进来。
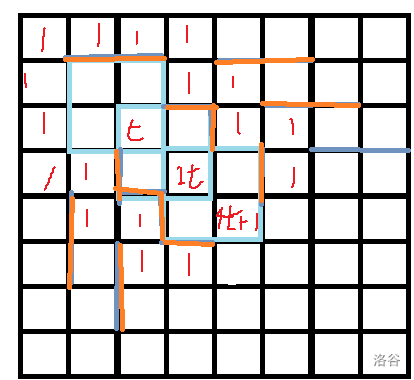
(那些蓝色的方格就是每次递推)
外面的橙墙保证外围的都是 \(1\)。
然而 \(2^{50}\) 不到 \(10^{18}\),我们需要优化!
把 \(2 \cdot 2\) 改成 \(3 \cdot 3\),继续开始优化。
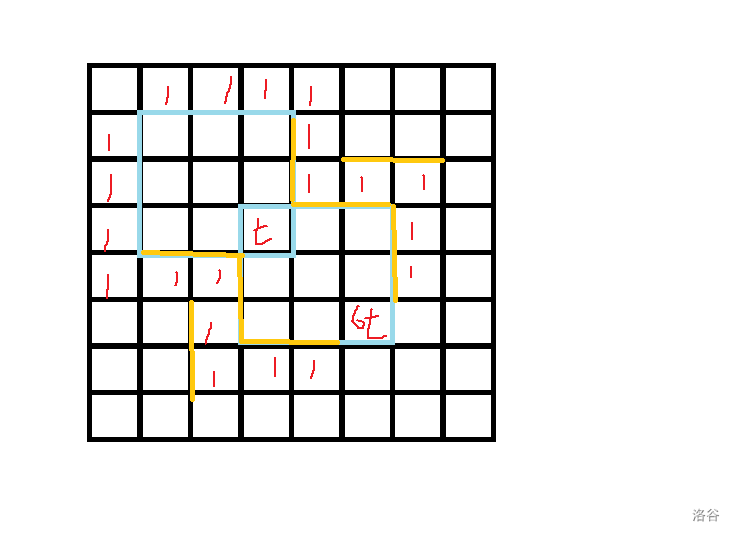
\(6t\) 有了,接着要凑出余数了。
注意到两边的黄门,把它们打开,就能增加 \(6t\)。
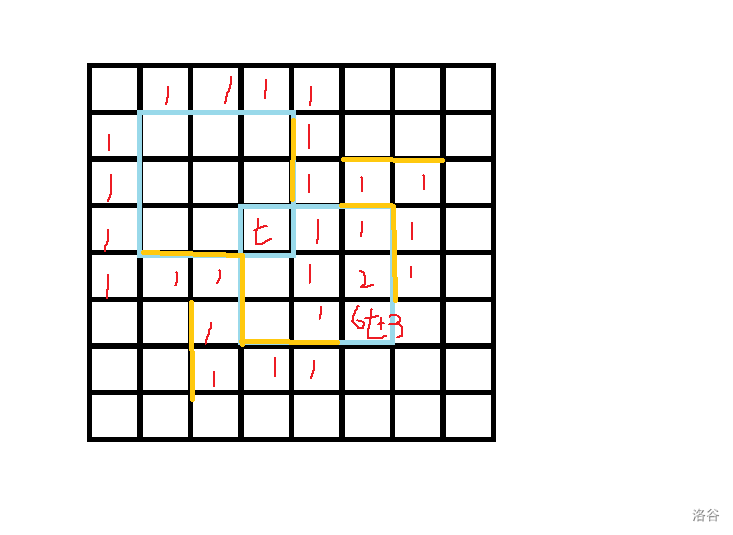
开这样的一扇门可以增加 \(3\),开与 \(6t\) 同行列的门可以增加 \(1\)。
于是就能拼出我们要的所有余数。
#include <cstdio>
#include <vector>
using namespace std;
const int M = 505;
struct tp {int x1, yy, x2, y2;};
int nx, ny; long long s; vector<tp> ans;
void dfs(long long k){
if(k == 0){
nx = 2; ny = 2;
ans.push_back({2, 1, 2, 2}); ans.push_back({1, 2, 2, 2});
return;
}
dfs(k/6);
ans.push_back({nx+2, ny-2, nx+2, ny-1}); ans.push_back({nx+3, ny-2, nx+3, ny-1});
ans.push_back({nx-2, ny+2, nx-1, ny+2}); ans.push_back({nx-2, ny+3, nx-1, ny+3});
ans.push_back({nx, ny+2, nx, ny+3}); ans.push_back({nx+1, ny+2, nx+1, ny+3});
ans.push_back({nx+2, ny, nx+3, ny}); ans.push_back({nx+2, ny+1, nx+3, ny+1});
int t = k % 6;
bool op[4] = {1, 1, 1, 1};
if(t >= 3) op[0] = 0, t -= 3;
if(t >= 1) op[1] = 0, --t;
if(t >= 1) op[3] = 0, --t;
if(op[0] == 1) ans.push_back({nx+1, ny-1, nx+1, ny});
if(op[1] == 1) ans.push_back({nx+2, ny-1, nx+2, ny});
if(op[2] == 1) ans.push_back({nx-1, ny+1, nx, ny+1});
if(op[3] == 1) ans.push_back({nx-1, ny+2, nx, ny+2});
nx += 2; ny += 2;
}
bool in(int x){
return 1 <= x && x <= nx;
}
int main(){
scanf("%lld", &s);
dfs(s);
printf("%d %d\n", nx, ny);
int cnt = 0;
for(int i = 0; i < ans.size(); i++){
if(in(ans[i].x1) && in(ans[i].yy) && in(ans[i].x2) && in(ans[i].y2)) ++cnt;
}
printf("%d\n", cnt);
for(int i = 0; i < ans.size(); i++){
if(in(ans[i].x1) && in(ans[i].yy) && in(ans[i].x2) && in(ans[i].y2))
printf("%d %d %d %d\n", ans[i].x1, ans[i].yy, ans[i].x2, ans[i].y2);
}
}