2023.4.7 Vergil 回归！

本次 Vergil 讲了很多很有意思的东西，今天我们来总结一下~

字典树 - Trie

顾名思义，一种像字典一样的树，用于应对字符串问题。

树的每一条边都代表一个字母，从根节点到任何一点的一条简单路径就代表了一个字符串。举个例子，从 \(1\) 到 \(13\) 的简单路径就对应了字符 cab。

简单？我们直接看一下 模板题 的代码。

朴素写法

首先，我们要建立单个字符到数字的映射关系，本题中包含 大小写字母 和 数字，当然，很多情况下只有小写字母，直接 -'a' 也是可以的。

建立映射：

int find(int x) {
	if(x>='0' && x<='9')	return x-'0'+1;
	else if(x>='A' && x<='Z')	return x-'A'+10+1;
	else if(x>='a' && x<='z')	return x-'a'+10+26+1;
}

接下来，我们要解决插入字符串，也很简单，遍历即可：

void insert(std::string s) {
	int now=1,len=s.length();
	for(int i=0;i<len;++i) {
		if(node[now][find(s[i])]) {
			now=node[now][find(s[i])];//node用于指向当前节点的子节点
			cnt[now]++;//cnt用于记录以从根到该点的路径所代表的字符串为前缀的字符串的数量
		}
		else {
			tot++;//tot用于记录总节点数
			now=node[now][find(s[i])]=tot;
			cnt[now]=1；
		}
	}
}

最后，查询，依然是简单粗暴的遍历：

int query(std::string s) {
	int now=1,len=s.length();
	for(int i=0;i<len;++i) {
		if(node[now][find(s[i])])	now=node[now][find(s[i])];
		else return 0;
	}
	return cnt[now];
}

这就是字典树的全部了……吗？

记住这是一道多测题，你需要初始化。什么？memset？相信我，你一定会 T 的。所以，我们有几种很新的方法。

优化：时间戳写法

这里我们引入一个新的变量 \(check_i\) ，记录节点 \(i\) 上一次更新是在哪一组数据。如果当前的数据组数与 \(check_i\) 不同，就初始化节点 \(i\)。选择性初始化时一个不错的降低复杂度的选择。

同时，我们初始化其实只需要重置 \(cnt\) 数组即可，因为我们可以一直沿用当前字典树结构。

\(AC \ CODE\)

#include<bits/stdc++.h>
const int N=3e6+6;
int node[N][65],cnt[N],tot=1,T,n,q,Time=0,check[N];
int find(int x) {
	if(x>='0' && x<='9')	return x-'0'+1;
	else if(x>='A' && x<='Z')	return x-'A'+10+1;
	else if(x>='a' && x<='z')	return x-'a'+10+26+1;
}
void insert(std::string s) {
	int now=1,len=s.length();
	for(int i=0;i<len;++i) {
		if(node[now][find(s[i])]) { 
			now=node[now][find(s[i])];
			if(check[now]==Time)	cnt[now]++;
			else	cnt[now]=1,check[now]=Time;
		}
		else {
			tot++;
			now=node[now][find(s[i])]=tot;
			cnt[now]=1,check[now]=Time;
		}
	}
}
int query(std::string s) {
	int now=1,len=s.length();
	for(int i=0;i<len;++i) {
		if(node[now][find(s[i])])	now=node[now][find(s[i])];
		else return 0;
	}
	return check[now]==Time?cnt[now]:0;
}
int main(){
	std::cin>>T;
	while(T--) {
		Time++;
		std::cin>>n>>q;
		for(int i=1;i<=n;++i) {
			std::string s;
			std::cin>>s;
			insert(s);
		}
		for(int i=1;i<=q;++i) {
			std::string s;
			std::cin>>s;
			std::cout<<query(s)<<'\n';
		}
	}
	return 0;
}

接下来我们见见更多的题。

更多题目

UVA11488 Hyper Prefix Sets

是的，我放的是洛谷的链接。因为考虑到 UVA 定时爆炸，放洛谷应该会方便些吧。这道题其实就是多了一个前缀长度，遍历所有节点算一下 \(cnt \times dep\) 的最大值就可以了。
不过不知道为什么我 T 了，后来改成 memset 奇迹的过了，所以推荐优化可以使用标记清空写法，时间戳有点费脑子。

HDU-1251 统计难题

放的 vjudge。没什么可说的，基本就是模板，但是注意因为判断插入和查询是空行，所以第一次输入可以用 getline，第二次记得让 while 循环停下来。

std::string s;
while(getline(std::cin,s)) {
	if(s=="")	break;
	insert(s);
}
while(getline(std::cin,s)) {
	if(s=="")	break;
	std::cout<<query(s)<<'\n';
}

P5335 [THUSC2016]补退选

这可是一道好题啊，好题啊。

我们考虑不需要上一次查询 ANS 的情况，如何查找前缀为 \(S\) 的学生数量超过要求 \(k\) 的最小事件数呢？

一种是暴力，一个事件查一次，复杂度爆炸；
另一种是我们可以使用一个 vector 记录，如 \(rec(i,k)\) 代表节点 \(i\) 第一次人数为 \(k\) 人时的事件数，最后查询要求的 \(rec(i,k)\) 即可。

接下来考虑在线，使用第二种方法，线性复杂度，绝对没问题。
建议在线查询，离线的话还需要判定你查询的结果是否大于当前事件数……挺难办的。

字典树就到这里了，接下来来说说搜索。

搜索

搜索也是讲了很多啊，一个一个来。

折半 - Meet in the Middle

考虑一个问题，有一个 \(n\) 个整数的集 \(S\)，问是否能从 \(S\) 中选取四个元素 \(a,b,c,d\)，使得 \(a+b+c+d=0\)。允许选取同一元素多次。

如果 \(n \leq 1000\)，直接暴力肯定就不好使了。\(n^4\) 必然会爆。所以，我们就要介绍一种新的方法：折半。

**前者是普通搜索，后者是折半搜索，是不是形象点了？

我们都知道，在搜索中，每迭代一层，其状态量是会指数级增加的。所以，控制住迭代的深度，就可以控制住时间复杂度。我们将这个集合分成两部分，分别进行遍历，然后再合并，得出结果，这个过程就是 折半。也可以理解为，我们通过存储中间信息，做到了空间换时间。因为折半搜索迭代层数只有暴力的一半，所以这道题中复杂度缩减到了 \(O(2n^2)\)。

代表性的题型是 P3067 [USACO12OPEN]Balanced Cow Subsets G。

具体过程就是先求前一半的所有方案，然后再求后一半，合并后判断是否合法。

\(AC \ CODE\)

#include<bits/stdc++.h>
const int N=22;
int n,a[N],ans=0,d[(1<<20)+10];
struct plan_board {
	struct node {int plan,sum;};
	std::vector<node> v[200000];
	void push_back(int plan,int sum) {
		const int mod=114511;
		int t=sum%mod;
		if(sum<0)	t+=mod;
		v[t].push_back({plan,sum});
	}
	void count(int plan,int sum) {
		const int mod=114511;
		int t=sum%mod;
		if(sum<0)	t+=mod;
		for(auto l:v[t]) {
			if(l.sum!=sum)	continue;
			d[(l.plan<<(n-n/2))+plan]=1;
		}
	}
}b;//类似于哈希的储存方法，通过状态压缩枚举计划
void dfs(int sum,int pos,int plan,int part) {
	if(part==1 && pos==n/2+1)	{b.push_back(plan,sum);	return;}
	if(part==2 && pos==n+1)	{b.count(plan,sum);		return;}
	dfs(sum,pos+1,plan<<1,part);//不放
	dfs(sum+a[pos],pos+1,(plan<<1)+1,part);//放在左边的集合
	dfs(sum-a[pos],pos+1,(plan<<1)+1,part);//放在右边的集合
	return;
}
int main(){
	std::ios::sync_with_stdio(0);
	std::cin.tie(0);std::cout.tie(0);
	std::cin>>n;
	for(int i=1;i<=n;++i)
		std::cin>>a[i];
	dfs(0,1,0,1);
	dfs(0,n/2+1,0,2);
	for(int i=1;i<(1<<n);++i)	ans+=d[i];
	std::cout<<ans;
	return 0;
}

还有一道题，P3878 [TJOI2010]分金币，也和这道差不多。

爬山算法

本质上是一种贪心，随机起点，每次随机方向，夸步幅度指数递减，如果比当前点更优就走，否则就不动。

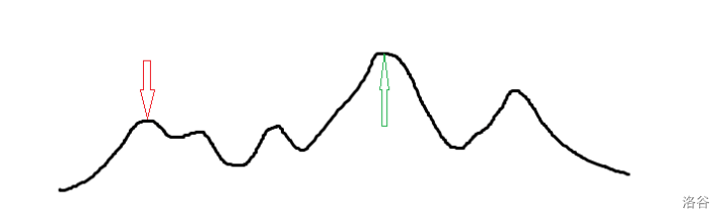
如图所示，登山其实是一种非常强的骗分方法，但是其容易受到次优解影响。所以，我们可以多次随机起点爬山，爬他个114514回。

模板是 P1337 [JSOI2004] 平衡点 / 吊打XXX，简直给我写精神内耗了。说一些要注意的点：

• 少用变量类型转换！转换同样费时间。
• rand() 的分布不一定均匀，所以数组中元素的顺序也会有关系。（指 dir 数组改一把顺序就 AC 了……活气死我。）你甚至可以写一个 srand((unsigned)time(0))，然后开始祈祷。
• 浮点型变量尽量少的使用中间变量，会造成精度损失。
• O2 对爬山枚举次数上限的提升特别大，不开 O2 这道题 80 次是比较保守的，开 O2 的话可以增加到 400 次，用时几乎一样（但是 \(rp\) 好的话 80 次就能 A）
• inline 是否任何时候都能提速，会不会反向优化，有待研究。
• 实在过不去，#define double long double 吧，你会很幸福。

\(AC \ CODE\)

#include<bits/stdc++.h>
#define sqr(x) ((x)*(x))
int dirx[8]={1,-1,0,0,1,-1,1,-1};
int diry[8]={0,0,1,-1,1,-1,-1,1};
int n,w[1005];
double x[1005],y[1005],cx[100],cy[100],ans[100];
inline double calc(int id,double nx,double ny) {
	double tmp=0;
	for(int i=1;i<=n;++i) {
		double dis=sqrt(sqr(x[i]-nx)+sqr(y[i]-ny));
		tmp+=dis*w[i];
		if(tmp>=ans[id]) break;
	}
	if(ans[id]>tmp) {cx[id]=nx,cy[id]=ny,ans[id]=tmp;}
	return tmp;
}
inline void climbing(int id) {
	ans[id]=1e20;
	cx[id]=rand()%20000-10000;
	cy[id]=rand()%20000-10000;
	ans[id]=calc(id,cx[id],cy[id]);
	for(double step=1e5;step>1e-4;step*=0.98) {
		int dir=rand()%8;
		calc(id,cx[id]+dirx[dir]*step,cy[id]+diry[dir]*step);
	}
}
int main(){
	std::ios::sync_with_stdio(0);
	std::cin.tie(0);std::cout.tie(0);
	std::cin>>n;
	for(int i=1;i<=n;++i)
		std::cin>>x[i]>>y[i]>>w[i];
	for(int i=1;i<=80;++i)	climbing(i);
	int id=1;
	for(int i=2;i<=80;++i) {
		if(ans[id]>ans[i]) id=i;
	}
	printf("%.3f %.3f\n",cx[id],cy[id]);
	return 0;
}

模拟退火 - Simulated Annealing, SA

“模拟退火算法来源于固体退火原理，是一种基于概率的算法，将固体加温至充分高，再让其徐徐冷却，加温时，固体内部粒子随温升变为无序状，内能增大，而徐徐冷却时粒子渐趋有序，在每个温度都达到平衡态，最后在常温时达到基态，内能减为最小。”

由上文可得，模拟退火相较于同为玄学的爬山算法比较墨迹，所以我们以后再学。（）

Vergil 讲述的新知识大概就是这些了，高二的 OI 生涯已经结束，新高一的我们将接过学长们的火炬，继续为 TSOI 而战！