拓扑排序 - TopoSort
前言
wcy 终于考上了心仪的大学,开启了精彩的大学生活!然而光是选课这一件事就把他难住了,因为一些课程包含先修课程:
| 课程编号 | 课程名称 | 先修课程 |
|---|---|---|
| C1 | 高等数学 | 无 |
| C2 | 程序设计基础 | 无 |
| C3 | 离散数学 | C1,C2 |
| C4 | 数据结构 | C2,C3 |
| C5 | 算法语言 | C2 |
| C6 | 编译技术 | C4,C5 |
| C7 | 操作系统 | C4,C9 |
| C8 | 普通物理 | C1 |
| C9 | 计算机原理 | C8 |
wcy 想排出一个顺序,让他可以丝滑地上完这九科课,那么这个顺序应该怎么排呢?
概念
AOV网
用节点表示活动,用弧表示活动之间的优先关系的有向图,叫做AOV网,即Activity On Vertex Network。
比如前言中给到的这个课程表,我们可以以图的形式把他画出来: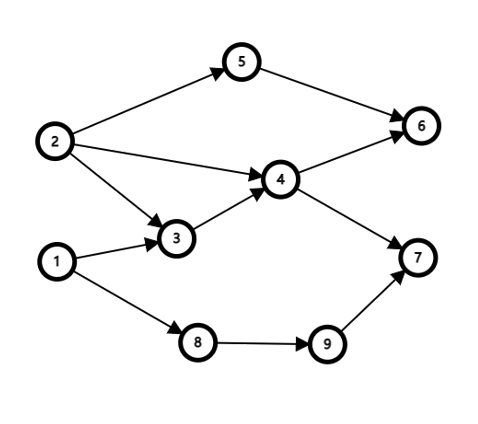
这就是一个AOV网。
拓扑排序
拓扑排序指将AOV网中的节点排成一个线性序列,该序列必须满足:若从节点 \(i\) 到节点 \(j\) 有一条路径,则在该序列中节点 \(i\) 一定在节点 \(j\) 之前。
不难发现,如果一个AOV网有环,就必然无法得到这个AOV网的拓扑排序,因为他必然出现自己是自己前驱的情况。
所以,对有向图的节点进行拓扑排序后,如果所有节点都在拓扑序列中,那么就可以说明这个AOV网必然无环。
该AOV网是无环有向图 & 该AOV网可进行拓扑排序 互为充要条件。
实践
实现方法
大致分为两步走:
- 找入度为0的点
- 将该点纳入拓扑序列,在图中删除该点和该点的所有边
重复这个操作。
其间,我们可能需要一个中间容器储存所有入度为零且尚未纳入序列的点。这个容器依使用情况而定,栈、队列、优先队列均可。(甚至有时候可以不需要中间容器,每次处理时都搜一次点,甚至可以通过用DFS辅助等方法排序,用好有奇效哦)
代码
以栈为例的代码附上:
#include<bits/stdc++.h>
using namespace std;
int n,m,topo[MAXN],indegree[MAXN];
bool edge[MAXN][MAXN];
stack<int> s;
void TopoSort()
{
int cnt=0;
for(int i=1;i<=n;++i)
{
if(indegree[i]==0)
s.push(i);
}
while(!s.empty())
{
int u=s.top();
s.pop();
topo[++cnt]=u;
for(int j=1;j<=n;++j)
if(edge[u][j])
if(--indegree[j]==0)
s.push(j);
}
}
int main()
{
scanf("%d%d",&n,&m);
memset(edge,0,sizeof(edge));
memset(indegree,0,sizeof(indegree));
for(int i=1;i<=m;++i)
{
int u,v;
scanf("%d%d",&u,&v);
edge[u][v]=1;
indegree[v]++;
}
TopoSort();
for(int i=1;i<=n;++i)
printf("%d ",topo[i]);
return 0;
}
将前言中的例子送进来,就可以得到他的一个拓扑序列如图:
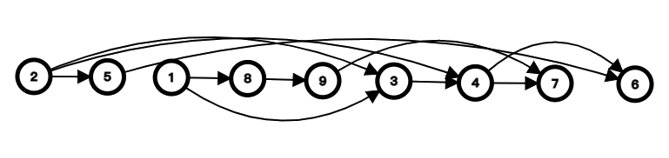
这样拓扑序列的特点就一目了然了。图中所有的箭头方向向后。
不唯一性
或者其实还有其他的拓扑序列:
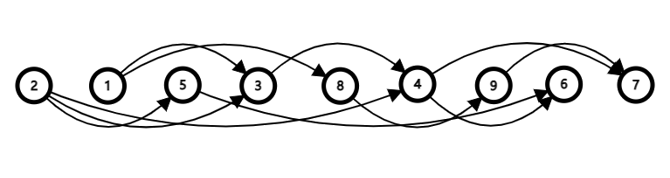
所以可见,一个AOV网的拓扑序列是不唯一的。
关于写法
其实拓扑的写法还是很自由的,所以我们还可以通过其他方法来实现toposort.
比如使用搜索的写法——dfs:
#include<bits/stdc++.h>
using namespace std;
int n,m,indegree[MAXN],topo[MAXN];
stack<int>s;
vector<int>edge[MAXN];
bool dfs(int dep)
{
if(dep>n) return 1;
if(dep==1)
for(int i=1;i<=n;++i)
if(!indegree[i])
s.push(i);
if(s.empty()) return 0;
int u=s.top();
s.pop();
indegree[u]=-1;
topo[dep]=u;
for(int i=0;i<edge[u].size();++i)
if(--indegree[edge[u][i]]==0)
s.push(edge[u][i]);
return dfs(dep+1);
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=m;++i)
{
int u,v;
scanf("%d%d",&u,&v);
edge[u].push_back(v);
indegree[v]++;
}
if(dfs(1))
for(int i=1;i<=n;++i)
printf("%d ",topo[i]);
else
printf("Impossible.");
return 0;
}
当然,你甚至可以每次搜一遍入度,抛弃中间容器,这里就展示一种:
bool dfs(int dep)
{
if(dep>n) return 1;
int temp=-1;
for(int i=1;i<=n;++i)
if(!indegree[i]) {temp=i; break;}
if(temp==-1) return 0;
indegree[temp]=-1;
topo[dep]=temp;
for(int i=0;i<edge[temp].size();++i)
indegree[edge[temp][i]]--;
return dfs(dep+1);
}
判断重边
对于邻接矩阵的存图方法,由于采用布尔值存图,重边会导致入度增加而邻接矩阵不变,必然出事。所以邻接矩阵请务必判重边。
if(!edge[u][v])
{
edge[u][v]=1;
indegree[v]++;
}
而邻接表,如 vector 存图则不需要判重,这是因为我们使用 vector 存图通常是存该点的子节点,所以在出现重边时该子节点在入度数组和 vector 中都会被记录两次,也就不会出现这个问题了。 (vector存图见上面dfs写法)
小题练手
NO.1 模板题 - 给火星人明明辈分
一道非常简单的板子题
NO.2 换个方式存图
反向建边,vector 存图,优先队列作容器,细节拉满。
NO.3 抓住 Toposort 的特点
这道题把握拓扑排序的核心步骤:检查入度为0的点。另外需要多测进行topo。
NO.4 Topo 全排列
Topo + DFS 可以想一下当初写全排列怎么写的
NO.5 拓上 DP(doge)
又是你们喜欢的DP哈哈哈哈哈
NO.6 绕个小弯
需要变通一下,非常有意思的一道题
NO.7 CCF 荣誉出品「君のNOIP」
果然是 NOIP 的题,,,就非常的离谱啊,他甚至卡 ull。所以现在面前的就只有四个选择了:
- 高精度
- 使用 64 位 GCCG++ 的
_int128 - 其实有一种方法,由于题中提到 \(d[i]≤5\) ,所以 其实所有出现的分数的分母都有且只有 2,3,5 这几个质因数,所以自然可以拆成这三个数的幂相乘的形式,也就解决了分母的高精危机。详见大佬123456zmy的题解 P7113 【排水系统】
聪明的放弃最后一个点,在写完gcd等一系列分数运算后用long long拿到 90pts 卷铺盖走人。