\(Preface\)
主要是想刷点咕值然后就写了一写。。。顺便扔到博客园这边。
题解
这道题嘛..主要还是找性质推规律。
拿到题,第一眼:噢噢爆搜啊。
第二眼:噢噢贪心啊。
第三眼:很好贪心假了。然后苦思冥想半个小时去看题解。
看到兔队的题解直接蚌了。二分图?
仔细思考了一下也是。\(x\text{、}y\) 坐标显然可以分成两个没有直接边相连的集合,而我们要做的就是将给出的点的 \(x\text{、}y\) 坐标连边,找规律。
考虑这样一张图。
# * * *
# # * *
* * * #
(#是已有的元素,*是空)
画成二分图是这样的:
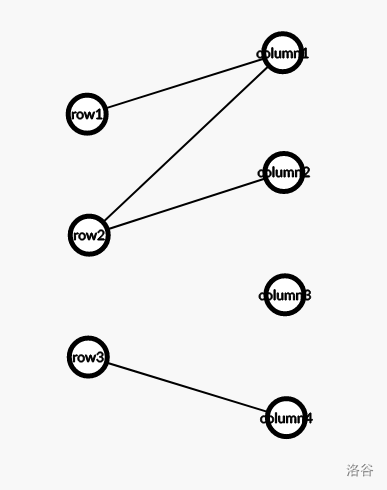
然后我们把能够合成的点都合成一下,变成了这样:
# # * *
# # * *
* * * #
再画一下二分图:
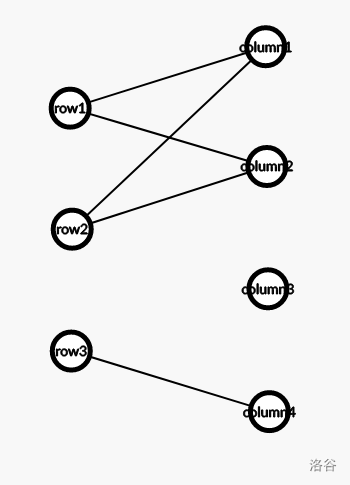
发现了一个小规律。就是说能够拓展的点加入后对原图的连通性不产生影响,不过似乎这个规律并不是我们想要找的最终规律,我们且称这个规律为规律一。
那么继续探索。
如果我们在 \(row_3\) 和 \(column2\) 之间连一条边,也就是买一个元素 \((3,2)\),图会变成这样:
# # * *
# # * *
* # * #
拓展一下变成:
# # * #
# # * #
# # * #
如果只画给出的点和新买的点,二分图为:
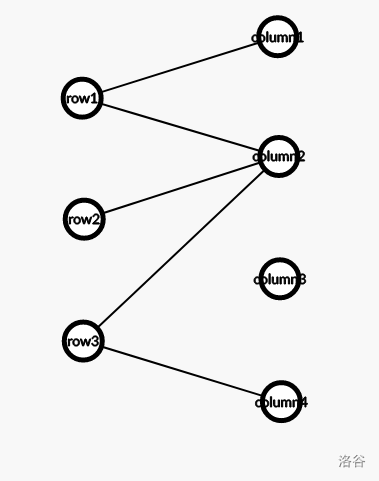
如果画上新拓展的点,二分图变为:
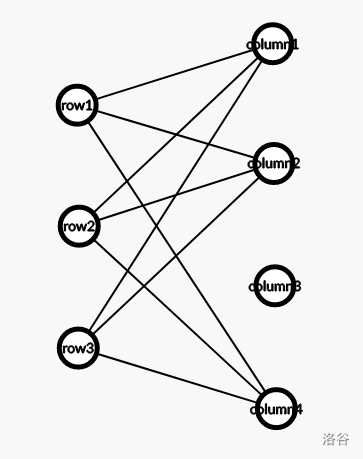
然后发现了规律:如果某一行和某一列是联通的(不一定直接有边相连),那么他们之间就将会有边直接相连。
考虑这个规律的实际意义。
有边直接相连就代表着这个点 \((row_i,column_j)\) 在图中是已经获得的元素。那么如果整张图是联通的,那是不是意味着所有的点就都是已经获得的元素?!
确实如此。那么称这个规律为规律二,这就是我们想要找的最终规律。
那么我们想要的答案就是使得原图变为一个连通图的最小连边数,也就是联通分量数 \(-1\)。
至此此题就基本做完了。首先按照规律一,我们无需多余地去拓展,只需要将给出的点进行建边。建好边后直接求一下联通分量个数就好了。
\(Ps\):其实没必要把边建出来,直接用一个并查集维护即可。
#include <iostream>
#define GMY (520&1314)
#define FBI_OPENTHEDOOR(x) freopen(#x ".in", "r", stdin), freopen(#x ".out", "w", stdout);
#define re register int
#define char_phi signed
#define N 200005
using namespace std;
inline void Fastio_setup(){ios::sync_with_stdio(false); cin.tie(NULL), cout.tie(NULL);}
int n, m, num, jia, final_ans;
int fa[N<<1];
int find(int x){return ((fa[x] == x) ? (x) : (fa[x] = find(fa[x])));}
inline void work(){
cin >> n >> m >> num; jia = n;
for (re i = 1 ; i <= n+m ; ++ i)
fa[i] = i;
for (re i = 1, x, y ; i <= num ; ++ i){
cin >> x >> y;
x = find(x), y = find(y+jia);
fa[x] = y;
}
for (re i = 1 ; i <= n+m ; ++ i)
if (fa[i] == i)
final_ans ++;
cout << final_ans-1 << endl;
}
// #define IXINGMY
char_phi main(){
#ifdef IXINGMY
FBI_OPENTHEDOOR(a);
#endif
Fastio_setup();
work();
return GMY;
}