首页 > 其他分享 >并查集概述

并查集概述

时间：2023-05-04 19:13:00浏览次数：43  
标签：查集 parent int 元素 find qRoot 概述 节点

 

 

并查集基础

一、概念及其介绍

并查集是一种树型的数据结构，用于处理一些不相交集合的合并及查询问题。

并查集的思想是用一个数组表示了整片森林（parent），树的根节点唯一标识了一个集合，我们只要找到了某个元素的的树根，就能确定它在哪个集合里。

二、适用说明

并查集用在一些有 N 个元素的集合应用问题中，我们通常是在开始时让每个元素构成一个单元素的集合，然后按一定顺序将属于同一组的元素所在的集合合并，其间要反复查找一个元素在哪个集合中。这个过程看似并不复杂，但数据量极大，若用其他的数据结构来描述的话，往往在空间上过大，计算机无法承受，也无法在短时间内计算出结果，所以只能用并查集来处理。

三、并查集的基本数据表示

如上图 0-4 下面都是 0，5-9 下面都是 1，表示 0、1、2、3、4 这五个元素是相连接的，5、6、7、8、9 这五个元素是相连的。

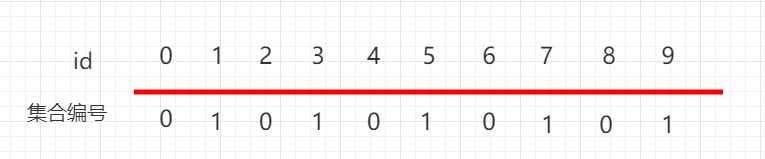
再如上图 0、2、4、6、8 下面都是 0 这个集合，表示 0、2、4、6、8 这五个元素是相连接的，1、3、5、7、9 下面都是 1 这个集合，表示 0，1、3、5、7、9 这五个元素是相连的。

构造一个类 UnionFind，初始化, 每一个id[i]指向自己, 没有合并的元素：

...
public UnionFind1(int n) {
        count = n;
        id = new int[n];
        // 初始化, 每一个id[i]指向自己, 没有合并的元素
        for (int i = 0; i < n; i++)
            id[i] = i;
    }
...

Java 实例代码

UnionFind.java 文件代码：

package runoob.union;

public class UnionFind{
    private int[] id;
    // 数据个数
    private int count;

    public UnionFind1(int n) {
        count = n;
        id = new int[n];
        for (int i = 0; i < n; i++)
            id[i] = i;
    }

}  

并查集快速查找

本小节基于上一小节并查集的结构介绍基础操作，查询和合并和判断是否连接。

查询元素所在的集合编号，直接返回 id 数组值，O(1) 的时间复杂度。

...
private int find(int p) {
    assert p >= 0 && p < count;
    return id[p];
}
...

合并元素 p 和元素 q 所属的集合， 合并过程需要遍历一遍所有元素, 再将两个元素的所属集合编号合并，这个过程是 O(n) 复杂度。

...
public void unionElements(int p, int q) {
    int pID = find(p);
    int qID = find(q);
    if (pID == qID)
        return;
    for (int i = 0; i < count; i++)
        if (id[i] == pID)
            id[i] = qID;
}
...

Java 实例代码

源码包下载：Download

UnionFind1.java 文件代码：

package runoob.union;

/**
 * 第一版union-Find
 */
public class UnionFind1 {
    // 我们的第一版Union-Find本质就是一个数组
    private int[] id;
    // 数据个数
    private int count;

    public UnionFind1(int n) {
        count = n;
        id = new int[n];
        // 初始化, 每一个id[i]指向自己, 没有合并的元素
        for (int i = 0; i < n; i++)
            id[i] = i;
    }

    // 查找过程, 查找元素p所对应的集合编号
    private int find(int p) {
        assert p >= 0 && p < count;
        return id[p];
    }

    // 查看元素p和元素q是否所属一个集合
    // O(1)复杂度
    public boolean isConnected(int p, int q) {
        return find(p) == find(q);
    }

    // 合并元素p和元素q所属的集合
    // O(n) 复杂度
    public void unionElements(int p, int q) {

        int pID = find(p);
        int qID = find(q);

        if (pID == qID)
            return;

        // 合并过程需要遍历一遍所有元素, 将两个元素的所属集合编号合并
        for (int i = 0; i < count; i++)
            if (id[i] == pID)
                id[i] = qID;
    }
}  

并查集快速合并

 

对于一组数据，并查集主要支持两个动作：

  • union(p,q) - 将 p 和 q 两个元素连接起来。

  • find(p) - 查询 p 元素在哪个集合中。

  • isConnected(p,q) - 查看 p 和 q 两个元素是否相连接在一起。

在上一小节中，我们用 id 数组的形式表示并查集，实际操作过程中查找的时间复杂度为 O(1)，但连接效率并不高。

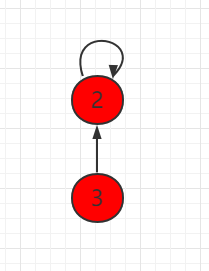
本小节，我们将用另外一种方式实现并查集。把每一个元素，看做是一个节点并且指向自己的父节点，根节点指向自己。如下图所示，节点 3 指向节点 2，代表 3 和 2 是连接在一起的，节点2本身是根节点，所以指向自己。

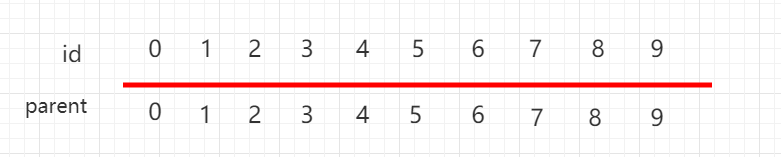
同样用数组表示并查集，但是下面一组元素用 parent 表示当前元素指向的父节点，每个元素指向自己，都是独立的。

如果此时操作 union(4,3)，将元素 4 指向元素 3：

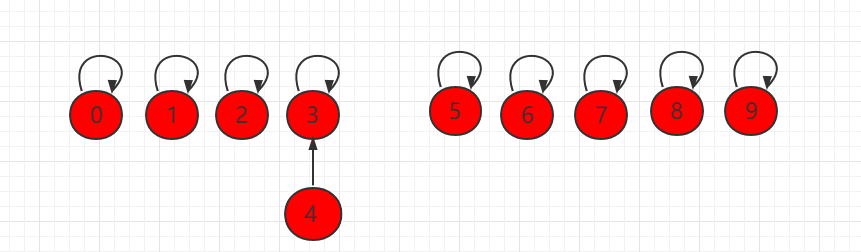
数组也进行相应改变：

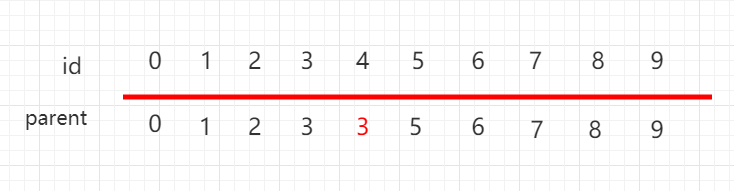
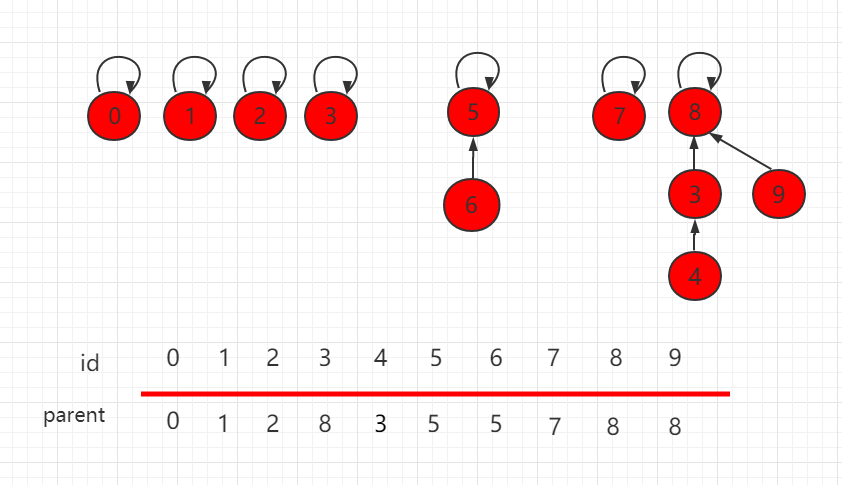
判断两个元素是否连接，只需要判断根节点是否相同即可。

如下图，节点 4 和节点 9 的根节点都是 8，所以它们是相连的。

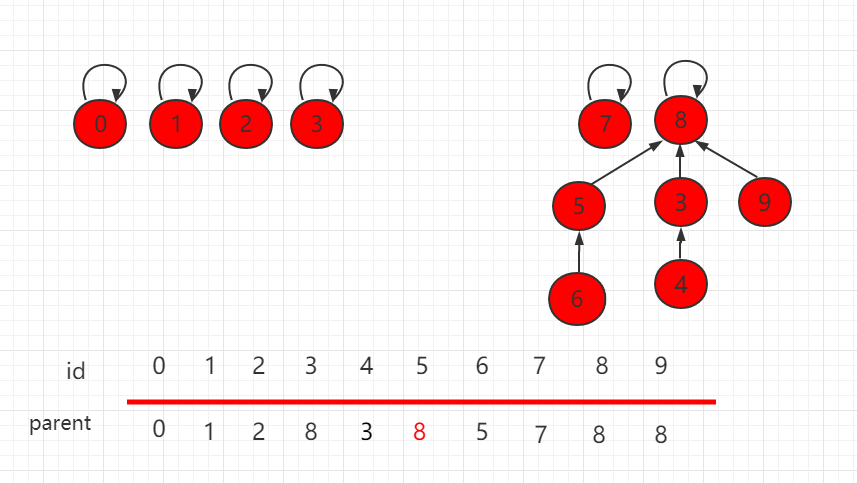
连接两个元素，只需要找到它们对应的根节点，使根节点相连，那它们就是相连的节点。

假设要使上图中的 6 和 4 相连，只需要把 6 的根节点 5 指向 4 的根节点 8 即可。

构建这种指向父节点的树形结构， 使用一个数组构建一棵指向父节点的树，parent[i] 表示 i 元素所指向的父节点。

...
private int[] parent;
private int count;  // 数据个数
...

查找过程, 查找元素 p 所对应的集合编号，不断去查询自己的父亲节点, 直到到达根节点，根节点的特点 parent[p] == p，O(h) 复杂度, h 为树的高度。

...
private int find(int p){
    assert( p >= 0 && p < count );
    while( p != parent[p] )
        p = parent[p];
    return p;
}
...

合并元素 p 和元素 q 所属的集合，分别查询两个元素的根节点，使其中一个根节点指向另外一个根节点，两个集合就合并了。这个操作是 O(h) 的时间复杂度，h 为树的高度。

public void unionElements(int p, int q){
    int pRoot = find(p);
    int qRoot = find(q);
    if( pRoot == qRoot )
        return;
    parent[pRoot] = qRoot;
}

Java 实例代码

源码包下载：Download

UnionFind2.java 文件代码：

package runoob.union;
/**
 * 第二版unionFind
 */
public class UnionFind2 {
    // 我们的第二版Union-Find, 使用一个数组构建一棵指向父节点的树
    // parent[i]表示第一个元素所指向的父节点
    private int[] parent;
    private int count;  // 数据个数
    // 构造函数
    public UnionFind2(int count){
        parent = new int[count];
        this.count = count;
        // 初始化, 每一个parent[i]指向自己, 表示每一个元素自己自成一个集合
        for( int i = 0 ; i < count ; i ++ )
            parent[i] = i;
    }
    // 查找过程, 查找元素p所对应的集合编号
    // O(h)复杂度, h为树的高度
    private int find(int p){
        assert( p >= 0 && p < count );
        // 不断去查询自己的父亲节点, 直到到达根节点
        // 根节点的特点: parent[p] == p
        while( p != parent[p] )
            p = parent[p];
        return p;
    }
    // 查看元素p和元素q是否所属一个集合
    // O(h)复杂度, h为树的高度
    public boolean isConnected( int p , int q ){
        return find(p) == find(q);
    }
    // 合并元素p和元素q所属的集合
    // O(h)复杂度, h为树的高度
    public void unionElements(int p, int q){
        int pRoot = find(p);
        int qRoot = find(q);
        if( pRoot == qRoot )
            return;
        parent[pRoot] = qRoot;
    }
}  

并查集 size 的优化

按照上一小节的思路，我们把如下图所示的并查集，进行 union(4,9) 操作。

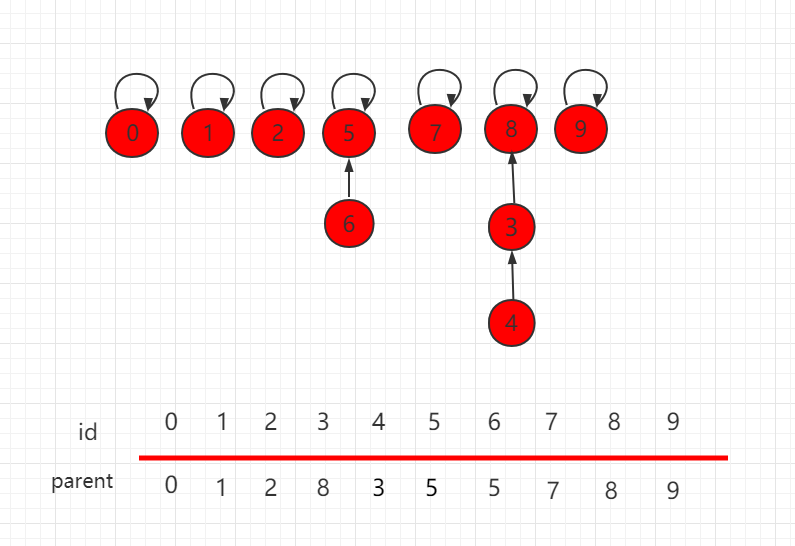
合并操作后的结构为：

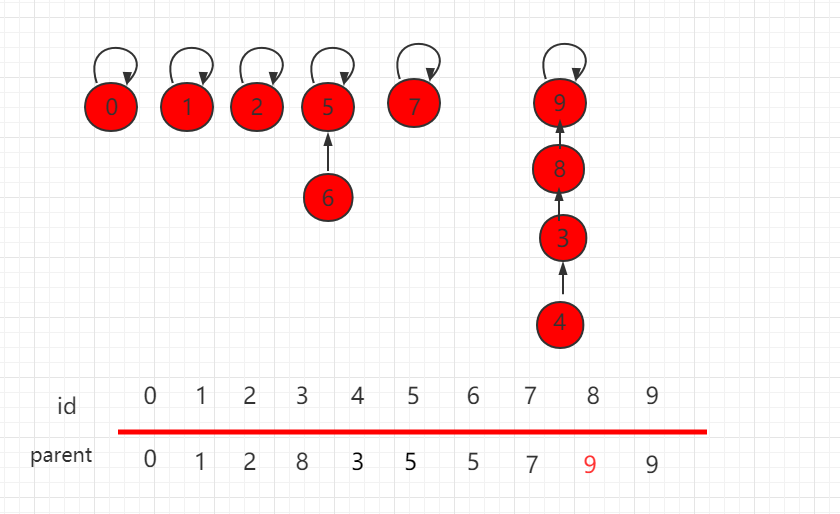
可以发现，这个结构的树的层相对较高，若此时元素数量增多，这样产生的消耗就会相对较大。解决这个问题其实很简单，在进行具体指向操作的时候先进行判断，把元素少的集合根节点指向元素多的根节点，能更高概率的生成一个层数比较低的树。

构造并查集的时候需要多一个参数，sz 数组，sz[i] 表示以 i 为根的集合中元素个数。

// 构造函数
public UnionFind3(int count){
    parent = new int[count];
    sz = new int[count];
    this.count = count;
    // 初始化, 每一个parent[i]指向自己, 表示每一个元素自己自成一个集合
    for( int i = 0 ; i < count ; i ++ ){
        parent[i] = i;
        sz[i] = 1;
    }
}

在进行合并操作时候，根据两个元素所在树的元素个数不同判断合并方向。

public void unionElements(int p, int q){
    int pRoot = find(p);
    int qRoot = find(q);
    if( pRoot == qRoot )
        return;
    if( sz[pRoot] < sz[qRoot] ){
        parent[pRoot] = qRoot;
        sz[qRoot] += sz[pRoot];
    }
    else{
        parent[qRoot] = pRoot;
        sz[pRoot] += sz[qRoot];
    }
}

优化后，合并结果如下，9 指向父节点 8。

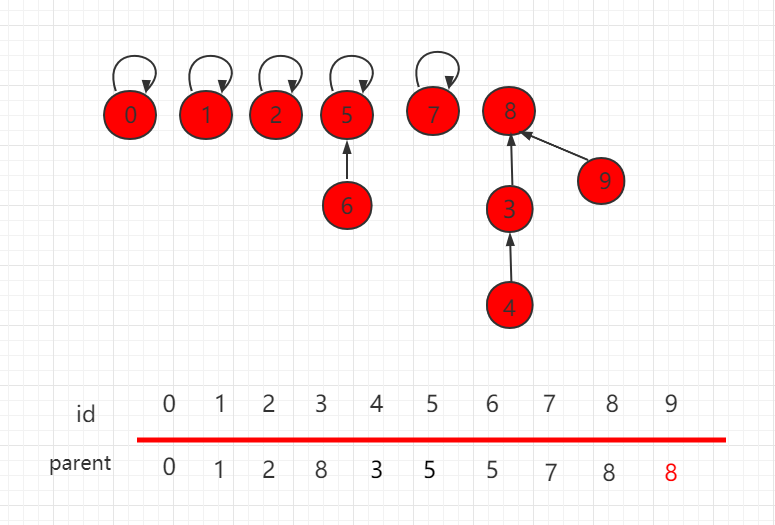
Java 实例代码

源码包下载：Download

UnionFind3.java 文件代码：

package runoob.union;

/**
 * 并查集size的优化
 */
public class UnionFind3 {
    // parent[i]表示第一个元素所指向的父节点
    private int[] parent;
    // sz[i]表示以i为根的集合中元素个数
    private int[] sz;
    // 数据个数
    private int count;

    // 构造函数
    public UnionFind3(int count){
        parent = new int[count];
        sz = new int[count];
        this.count = count;
        // 初始化, 每一个parent[i]指向自己, 表示每一个元素自己自成一个集合
        for( int i = 0 ; i < count ; i ++ ){
            parent[i] = i;
            sz[i] = 1;
        }
    }

    // 查找过程, 查找元素p所对应的集合编号
    // O(h)复杂度, h为树的高度
    private int find(int p){
        assert( p >= 0 && p < count );
        // 不断去查询自己的父亲节点, 直到到达根节点
        // 根节点的特点: parent[p] == p
        while( p != parent[p] )
            p = parent[p];
        return p;
    }

    // 查看元素p和元素q是否所属一个集合
    // O(h)复杂度, h为树的高度
    public boolean isConnected( int p , int q ){
        return find(p) == find(q);
    }

    // 合并元素p和元素q所属的集合
    // O(h)复杂度, h为树的高度
    public void unionElements(int p, int q){
        int pRoot = find(p);
        int qRoot = find(q);
        if( pRoot == qRoot )
            return;
        // 根据两个元素所在树的元素个数不同判断合并方向
        // 将元素个数少的集合合并到元素个数多的集合上
        if( sz[pRoot] < sz[qRoot] ){
            parent[pRoot] = qRoot;
            sz[qRoot] += sz[pRoot];
        }
        else{
            parent[qRoot] = pRoot;
            sz[pRoot] += sz[qRoot];
        }
    }
}    

并查集 rank 的优化

上一小节介绍了并查集基于 size 的优化，但是某些场景下，也会存在某些问题，如下图所示，操作 union(4,2)。

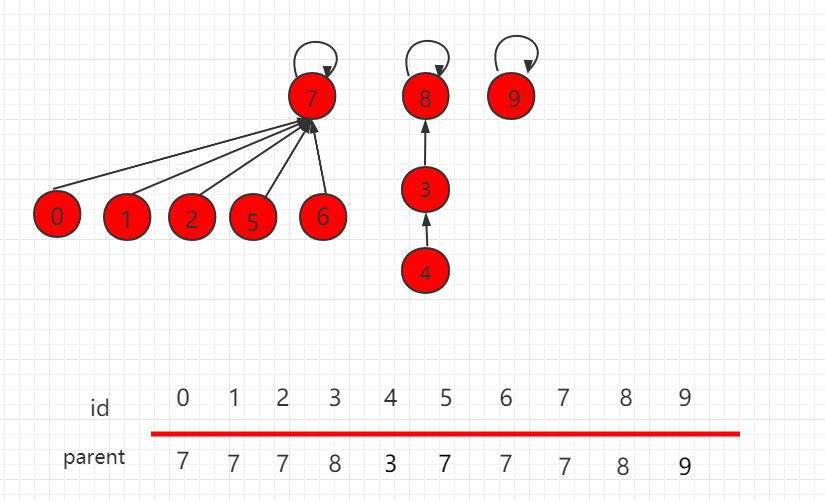
根据上一小节，size 的优化，元素少的集合根节点指向元素多的根节点。操完后，层数变为4，比之前增多了一层，如下图所示：

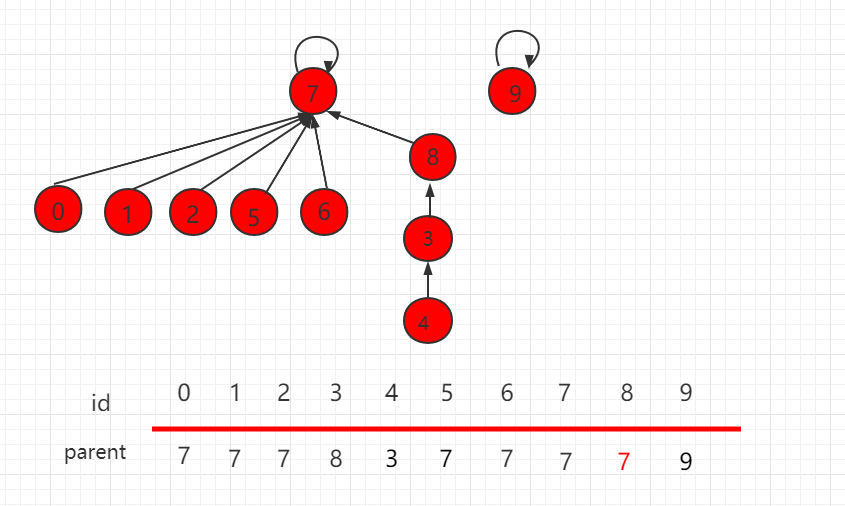
由此可知，依靠集合的 size 判断指向并不是完全正确的，更准确的是，根据两个集合层数，具体判断根节点的指向，层数少的集合根节点指向层数多的集合根节点，如下图所示，这就是基于 rank 的优化。

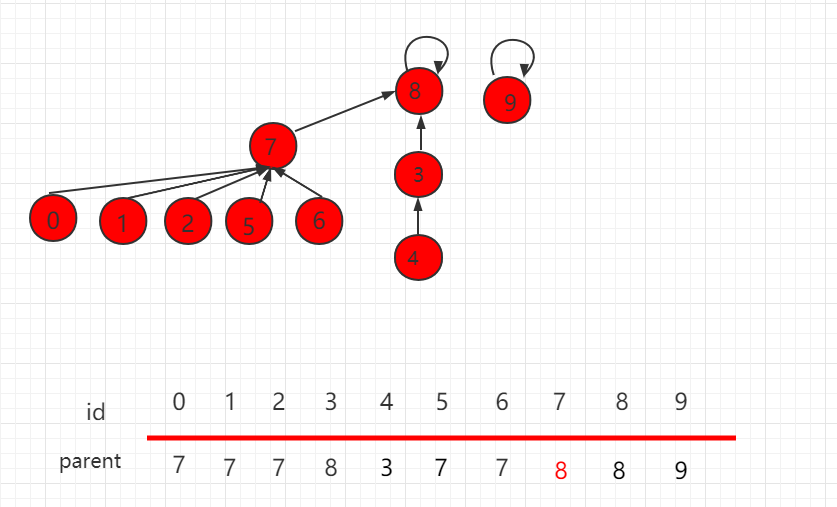
我们在并查集的属性中，添加 rank 数组，rank[i] 表示以 i 为根的集合所表示的树的层数。

...
private int[] rank;   // rank[i]表示以i为根的集合所表示的树的层数
private int[] parent; // parent[i]表示第i个元素所指向的父节点
private int count;    // 数据个数
...

构造函数相应作出修改：

...
// 构造函数
public UnionFind4(int count){
    rank = new int[count];
    parent = new int[count];
    this.count = count;
    // 初始化, 每一个parent[i]指向自己, 表示每一个元素自己自成一个集合
    for( int i = 0 ; i < count ; i ++ ){
        parent[i] = i;
        rank[i] = 1;
    }
}
...

合并两元素的时候，需要比较根节点集合的层数，整个过程是 O(h)复杂度，h为树的高度。

...
public void unionElements(int p, int q){
    int pRoot = find(p);
    int qRoot = find(q);
    if( pRoot == qRoot )
        return;

    if( rank[pRoot] < rank[qRoot] ){
        parent[pRoot] = qRoot;
    }
    else if( rank[qRoot] < rank[pRoot]){
        parent[qRoot] = pRoot;
    }
    else{ // rank[pRoot] == rank[qRoot]
        parent[pRoot] = qRoot;
        rank[qRoot] += 1;   // 此时, 我维护rank的值
    }
}
...

Java 实例代码

源码包下载：Download

UnionFind3.java 文件代码：

package runoob.union;
/**
 * 基于rank的优化
 */
public class UnionFind4 {
    private int[] rank;   // rank[i]表示以i为根的集合所表示的树的层数
    private int[] parent; // parent[i]表示第i个元素所指向的父节点
    private int count;    // 数据个数
    // 构造函数
    public UnionFind4(int count){
        rank = new int[count];
        parent = new int[count];
        this.count = count;
        // 初始化, 每一个parent[i]指向自己, 表示每一个元素自己自成一个集合
        for( int i = 0 ; i < count ; i ++ ){
            parent[i] = i;
            rank[i] = 1;
        }
    }
    // 查找过程, 查找元素p所对应的集合编号
    // O(h)复杂度, h为树的高度
    private int find(int p){
        assert( p >= 0 && p < count );
        // 不断去查询自己的父亲节点, 直到到达根节点
        // 根节点的特点: parent[p] == p
        while( p != parent[p] )
            p = parent[p];
        return p;
    }
    // 查看元素p和元素q是否所属一个集合
    // O(h)复杂度, h为树的高度
    public boolean isConnected( int p , int q ){
        return find(p) == find(q);
    }
    // 合并元素p和元素q所属的集合
    // O(h)复杂度, h为树的高度
    public void unionElements(int p, int q){
        int pRoot = find(p);
        int qRoot = find(q);
        if( pRoot == qRoot )
            return;
        if( rank[pRoot] < rank[qRoot] ){
            parent[pRoot] = qRoot;
        }
        else if( rank[qRoot] < rank[pRoot]){
            parent[qRoot] = pRoot;
        }
        else{ // rank[pRoot] == rank[qRoot]
            parent[pRoot] = qRoot;
            rank[qRoot] += 1;   // 维护rank的值
        }
    }
}  

并查集路径压缩

并查集里的 find 函数里可以进行路径压缩，是为了更快速的查找一个点的根节点。对于一个集合树来说，它的根节点下面可以依附着许多的节点，因此，我们可以尝试在 find 的过程中，从底向上，如果此时访问的节点不是根节点的话，那么我们可以把这个节点尽量的往上挪一挪，减少数的层数，这个过程就叫做路径压缩。

如下图中，find(4) 的过程就可以路径压缩，让数的层数更少。

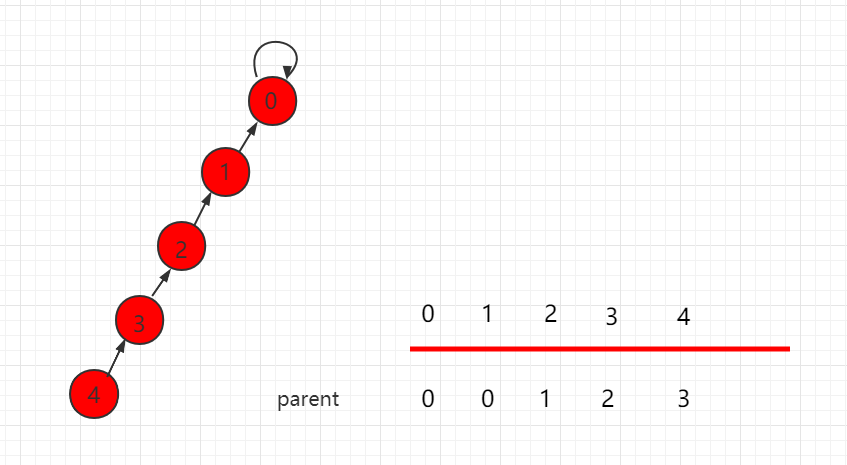
节点 4 往上寻找根节点时，压缩第一步，树的层数就减少了一层：

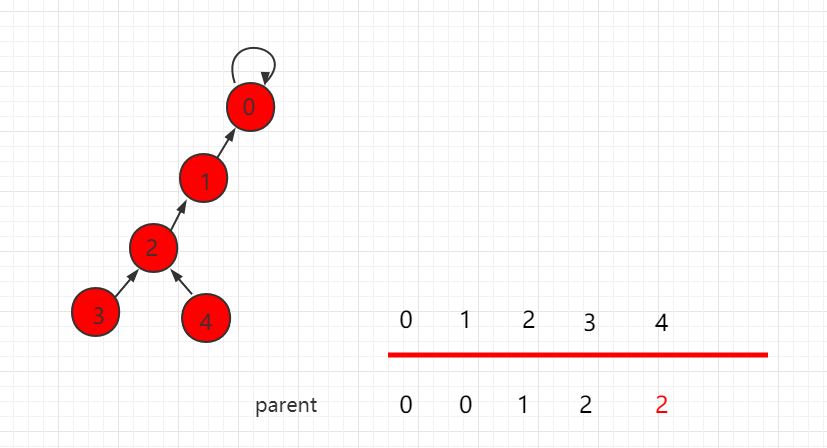
节点 2 向上寻找，也不是根节点，那么把元素 2 指向原来父节点的父节点，操后后树的层数相应减少了一层，同时返回根节点 0。

find 过程代码修改为 ：

// 查找过程, 查找元素p所对应的集合编号
// O(h)复杂度, h为树的高度
private int find(int p){
    assert( p >= 0 && p < count );

    // path compression 1
    while( p != parent[p] ){
        parent[p] = parent[parent[p]];
        p = parent[p];
    }
    return p;

}

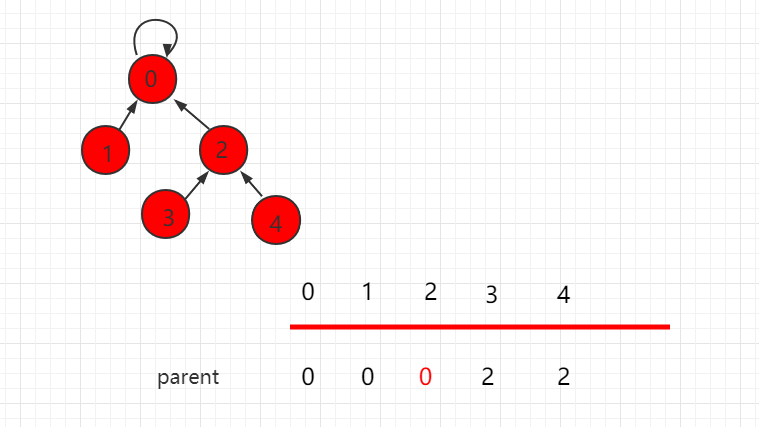
上述路径压缩并不是最优的方式，我们可以把最初的树压缩成下图所示，层数是最少的。

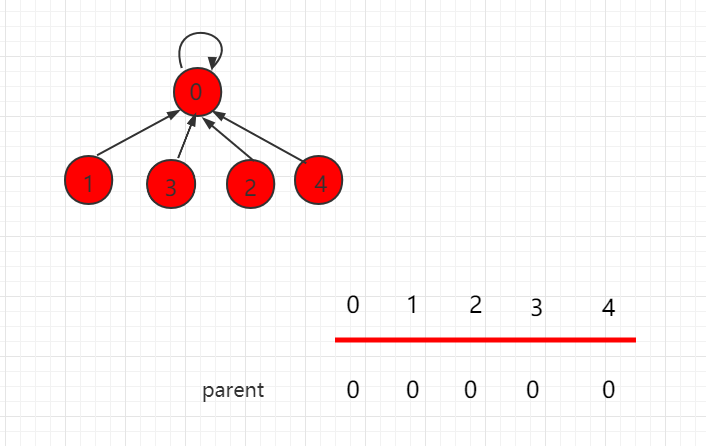
这个 find 过程代表表示为:

...
// 查找过程, 查找元素p所对应的集合编号
// O(h)复杂度, h为树的高度
private int find(int p) {
    assert (p >= 0 && p < count);

    //第二种路径压缩算法
    if (p != parent[p])
        parent[p] = find(parent[p]);
    return parent[p];
}
...

Java 实例代码

源码包下载：Download

UnionFind3.java 文件代码：

package runoob.union;

/**
 * 基于rank的优化
 */
public class UnionFind4 {

    private int[] rank;   // rank[i]表示以i为根的集合所表示的树的层数
    private int[] parent; // parent[i]表示第i个元素所指向的父节点
    private int count;    // 数据个数

    // 构造函数
    public UnionFind4(int count){
        rank = new int[count];
        parent = new int[count];
        this.count = count;
        // 初始化, 每一个parent[i]指向自己, 表示每一个元素自己自成一个集合
        for( int i = 0 ; i < count ; i ++ ){
            parent[i] = i;
            rank[i] = 1;
        }
    }

    // 查找过程, 查找元素p所对应的集合编号
    // O(h)复杂度, h为树的高度
    private int find(int p){
        assert( p >= 0 && p < count );
        // 不断去查询自己的父亲节点, 直到到达根节点
        // 根节点的特点: parent[p] == p
        while( p != parent[p] )
            p = parent[p];
        return p;

        //第二种路径压缩算法
        //if( p != parent[p] )
        //parent[p] = find( parent[p] );
        //return parent[p];
    }

    // 查看元素p和元素q是否所属一个集合
    // O(h)复杂度, h为树的高度
    public boolean isConnected( int p , int q ){
        return find(p) == find(q);
    }

    // 合并元素p和元素q所属的集合
    // O(h)复杂度, h为树的高度
    public void unionElements(int p, int q){

        int pRoot = find(p);
        int qRoot = find(q);

        if( pRoot == qRoot )
            return;

        if( rank[pRoot] < rank[qRoot] ){
            parent[pRoot] = qRoot;
        }
        else if( rank[qRoot] < rank[pRoot]){
            parent[qRoot] = pRoot;
        }
        else{ // rank[pRoot] == rank[qRoot]
            parent[pRoot] = qRoot;
            rank[qRoot] += 1;   // 维护rank的值
        }
    }
}

 

 

标签：查集,parent,int,元素,find,qRoot,概述,节点
From： https://www.cnblogs.com/shoshana-kong/p/17372223.html

相关文章

  • DAX：概述EARLIEST和EARLIER函数
    EARLIER函数用于访问外层行上下文，即使用外层行上下文，而不是最内层的行上下文检索列的值。EARLIER(<column>,<number>)EARLIEST(<column>)注意：EARLIER函数的第二个参数是可选的，默认值是1，表示要跳过的层数，可以向外跳过2层或多层行上下文。EARLIEST函数直接访问最外层的行上......
  • MySQL（十八）MySQL事务(一)：事务的概述与使用
    MySQL事务(一)：事务的概述与使用1数据库事务概述​ 事务是数据库区别于文件系统的重要特性之一，当我们有了事务就会让数据库始终保持一致性，同时我们还能通过事务的机制恢复到某个时间点，这样可以保证已提交到数据库的修改不会因为系统崩溃而丢失。1.1存储引擎支持情况​ show......
  • SAP系统PM模块概述-OVERVIEW
    1.SAP系统PM模块概述2.PM模块(含服务采购)组织架构3.PM模块主数据4.维护业务处理流程5.服务采购业务流程6.预防性维护业务流程7.信息系统&报表分析下一篇：SAPPM配置清单......
  • [Week 19]每日一题（C++，数学，并查集，动态规划）
    目录[Daimayuan]T1倒数第n个字符串（C++，进制）输入格式输出格式样例输入样例输出解题思路[Daimayuan]T2排队（C++，并查集）输入格式输出格式样例输入1样例输出1样例输入2样例输出2样例输入3样例输出3数据规模解题思路[Daimayuan]T3素数之欢（C++，BFS）数据规模输入格式输出格式样例输入样......
  • 第一章：概述
    1，因特网概述1.网络、互联网和英特网网络(Network)由若干结点(Node)和连接这些结点的链路(Link)组成。多个网络还可以通过路由器互连起来，这样就构成了一个覆盖范围更大的网络，即互联网（或互连网)。因此，互联网是“网络的网络(NetworkofNetworks)"。因特网(Internet)是世界......
  • 并查集的操作
    //并查集#include<stdio.h>#defineSIZE100intUFSets[SIZE];voidinitial(intS[])//初始化并查集全部设为-1即每一个元素都是独立的{for(inti=0;i<SIZE;i++){S[i]=-1;}}intFind(intS[],intx)//查找元素操作返回x所属根节点x指的是......
  • 带权并查集
    做了cf上一道题后发现我对并查集的理解不够深刻，顺带把带权并查集学一下。并查集初始化：对于一个集合A的所有元素，我们知道对于其中任意一个元素i，i€A。此时，我们可以认为i与A之间存在一条虚边，如果有新的元素要加入集合A，将该元素与A建一条边即可。这条边我们用数组fa[i]......
  • 三、JVM-运行时数据区概述及线程(基础篇)
    一、前言本节主要讲的是运行时数据区，也就是下图这部分，它是在类加载完成后的阶段当我们通过前面的：类的加载->链接(验证->准备->解析->)->初始化这几个阶段完成后，就会用到执行引擎对我们的类进行使用，同时执行引擎将会使用到我们运行时数据区也就是大厨做饭，我们把大厨后......
  • 01 ETH-以太坊概述
    《区块链技术与应用》课程链接：https://www.bilibili.com/video/BV1Vt411X7JF/?spm_id_from=333.337.search-card.all.click01ETH-以太坊概述目录01ETH-以太坊概述比特币区块链1.0，以太坊区块链2.0。比特币出块时间10分钟，以太坊出块时间十几秒，以太坊基于GHOST的共识协议改进......
  • 【pandas基础】--概述
    Pandas是一个开源的Python数据分析库。它提供了快速，灵活和富有表现力的数据结构，旨在使数据清洗和分析变得简单而快速。Pandas是基于NumPy数组构建的，因此它在许多NumPy函数上提供了直接的支持。它还提供了用于对表格数据进行操作的数据结构，例如Series和DataFrame。Pandas提供了......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99