题目
点这里看题目。
对于一个长度为 \(m\) 的、由互不相同整数组成的序列 \(a\),其为“连续”的当且仅当 \(\max a-\min a=m-1\),也即 \(a\) 的值构成整数上一个连续的区间。
给定正整数参数 \(n\),有 \(T\) 次询问。每次询问给出一个长度为 \(n\) 的正整数序列 \(L\),你需要求出满足下列条件的 \(1\sim n\) 的排列 \(p\) 的个数:
- 对于任意的 \(1\le r\le n\),\(p\) 以 \(r\) 结尾的“连续”区间的最大长度为 \(L_r\)。
答案对 \(998244353\) 取模。注意可能不存在符合条件的排列。
所有数据满足 \(1\le T\le 100, 1\le n\le 5\times 10^4\)。
分析
首先研究一下“连续”区间的性质:如果 \(I_1=[l_1,r_1]\) 和 \(I_2=[l_2,r_2]\) 是“连续”区间,且 \(I_1\cap I_2\neq \varnothing\),则 \(I_1\cup I_2\) 与 \(I_1\cap I_2\) 都是“连续”区间。
这说明,集合 \(\{[r-L_r+1,r]|1\le r\le n\}\) 中的两个区间要么包含,要么不交,那么一定会产生树形结构。
所以,如果 \(L_n\neq n\),或者区间之间不形成树形结构,答案就是 \(0\)。否则,一定可以构造出符合条件的排列。
我们进一步观察计数方法。首先考虑 \([1,n]\) 下面的儿子区间:
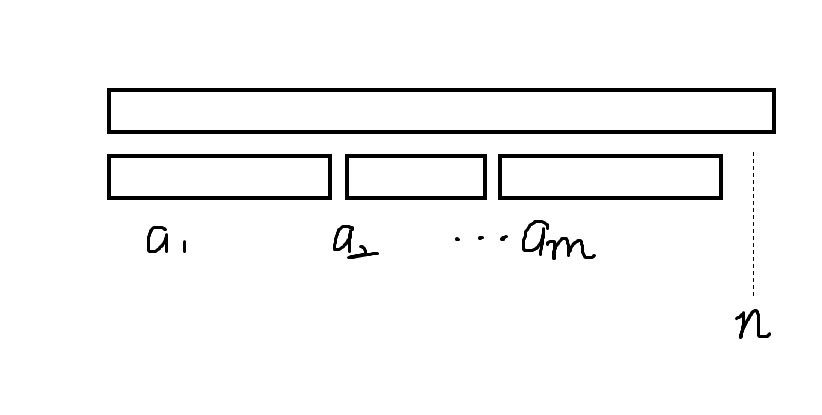
假如有 \(m\) 个儿子,长度分别为 \(a_1,a_2,\dots,a_m\),子树内部的方案数分别为 \(c_1,c_2,\dots,c_m\)。每个儿子区间对应的值区间均连续,因此我们仅需要考虑儿子的值区间的相对大小关系。当我们考虑跨儿子的区间时,首先肯定要求任意一段儿子区间并起来后不“连续”;其次,该条件满足后,可以证明不存在跨儿子区间的“连续”区间。那么,这一部分的方案数,就应该等于“令 \(n=m+1\),\(L_{m+1}=m+1\) 且 \(\forall 1\le i\le m,L_i=1\) 时,原问题的答案”,记其为 \(g_m\)。于是,此处答案就是 \(g_m\prod_{k=1}^mc_k\)。
注意到儿子的结构完全同构于 \([1,n]\) 处的结构。因此记 \(s_r\) 为区间 \([r-L_r+1,r]\) 下的儿子个数,答案就是 \(\prod_{r=1}^ng_r\)。
现在着力计算 \(g\)。我们注意到刚刚的讨论给出了一个递归构造排列的过程。设 \(F(x)=\sum_{n\ge 1}n!x^n\),也即非空排列的 OGF。那么,根据上述构造,我们可以知道 \(n!=[x^{n-1}]\sum_{m=0}^{n-1}g_mF(x)^m\)(对于 \(n\ge 1\))。于是,设 \(G(x)=\sum_{m\ge 0}g_mx^m\),我们不难得到复合方程:
\[xG[F(x)]=F(x) \]进一步地,改写成 \(x=\frac{F(x)}{G[F(x)]}\) 的形式,我们可知 \(H=\frac{x}{G}\) 为 \(F\) 的复合逆。此时就可以导出一个 \(O(n^2)\) 的算法。
你说得对,但是常数小估计也过不去。
复合方程很难处理,我们尝试转化成熟悉的微分方程的形式。
怎么下手呢?对于 \(G\) 直接求导只会让人更加困惑,并且丢掉了“复合”的联系。同时,我们注意到 \(F\) 有一个很简洁的微分方程(然而不是我注意到的):
\[F=x^2F'+xF+x \]能不能从它入手给出 \(G\) 的微分方程呢?Positive! 以下是详细推导:
\[\begin{aligned} x^2\frac{\text dF}{\text dx}+xF+x&=F\\ \frac{x^2}{G^2}\cdot \frac{\text dx}{\text d\frac{x}{G}}+\frac{x^2+x}{G}&=x\\ \frac{x^2}{G^2}\cdot \frac{G^2}{G-xG'}+\frac{x^2+x}{G}&=x\\ x^2G+(x^2+x)(G-xG')&=G(G-xG')x\\ G^2-xG'G-(2x+1)G+(x^2+x)G'&=0 \end{aligned} \]Remark.
对于变量间关系要有这样的理解......对于 OIer 来说还是太超前了一点
标签:le,const,int,领主,return,CTSC2018,inline,青蕈,mod From: https://www.cnblogs.com/crashed/p/17368120.html