2023-05-01:给你一个整数 n ,
请你在无限的整数序列 [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ...]
中找出并返回第 n 位上的数字。
1 <= n <= 2^31 - 1。
输入:n = 11
输出:0
解释:第 11 位数字在序列 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ... 里是 0 ,它是 10 的一部分。
答案2023-05-01:
该程序的大体过程:
1.定义数组 under 和 help,分别用于存储数字位数对应能处理的数的个数和指示各位数之间的跨度。
2.实现函数 findNthDigit,其输入为整数 n,表示要查找的数字在整数序列中的位置。根据 under 数组,找到包含第 n 个数字的区间长度 len,并返回调用子函数 number 的结果。
3.实现函数 number,其输入为当前路径 path、数字的位数 len、最高位的权重 offset、最低位的权重 all 和从开始算起剩余的第几个数字 nth。如果 offset 等于 0,则说明已经到达最低位,直接返回路径经过的值中的第 nth 个数字;否则,计算出当前节点 cur 取值(这可能需要根据 offset 来进行特殊处理),根据 all 和 offset 计算下一个节点的路径 cur*(all/offset)+path,并递归地调用 number 函数。
4.在 main 函数中,定义一个整数变量 n 表示要查找的数字在整数序列中的位置,调用 findNthDigit 函数查找第 n 个数字,并输出结果。
时间复杂度和空间复杂度如下:
1.findNthDigit 函数中的循环需要遍历数组 under,时间复杂度为 O(1) 平均时间复杂度为 O(log n);
2. number 函数实现了一个递归结构,每次递归除去常数项的时间复杂度为 O(1), 递归深度为 O(log n),所以总时间复杂度为 O(log n);
3.数组 under 和 help 的空间复杂度分别为 O(1),而递归调用 number 函数时,栈空间的最大使用量也为 O(log n)。因此,总的空间复杂度为 O(log n)。
综上所述,该算法的时间复杂度和空间复杂度均为 O(log n)。
go完整代码如下:
package main
var under = []int64{
0, 9, 189, 2889, 38889, 488889, 5888889, 68888889, 788888889, 8888888889, 98888888889,
}
var help = []int{
0,
1, // 1
10, // 2
100, // 3
1000, // 4
10000,
100000,
1000000,
10000000,
100000000,
1000000000,
}
func findNthDigit(n int) int {
l := 0
for i := 1; i < len(under); i++ {
if under[i] >= int64(n) {
l = i
break
}
}
return number(0, l, help[l], help[l], n-int(under[l-1]))
}
// path : 路径 左(低) <- 右(高)
// len : n -> 5位数 len = 5 固定!
// offset : 10000 目前要决定的是高1位
// 1000 目前要决定的是高2位
// 10 目前要决定的是高2位
// 可变
// all : 10000 固定
// nth : 第几个
func number(path, len, offset, all, nth int) int {
if offset == 0 {
return (path / help[nth]) % 10
} else {
j := (nth - 1) / (len * offset)
cur := 0
if offset == all {
cur = 1
}
cur += j
return number(cur*(all/offset)+path, len, offset/10, all, nth-j*len*offset)
}
}
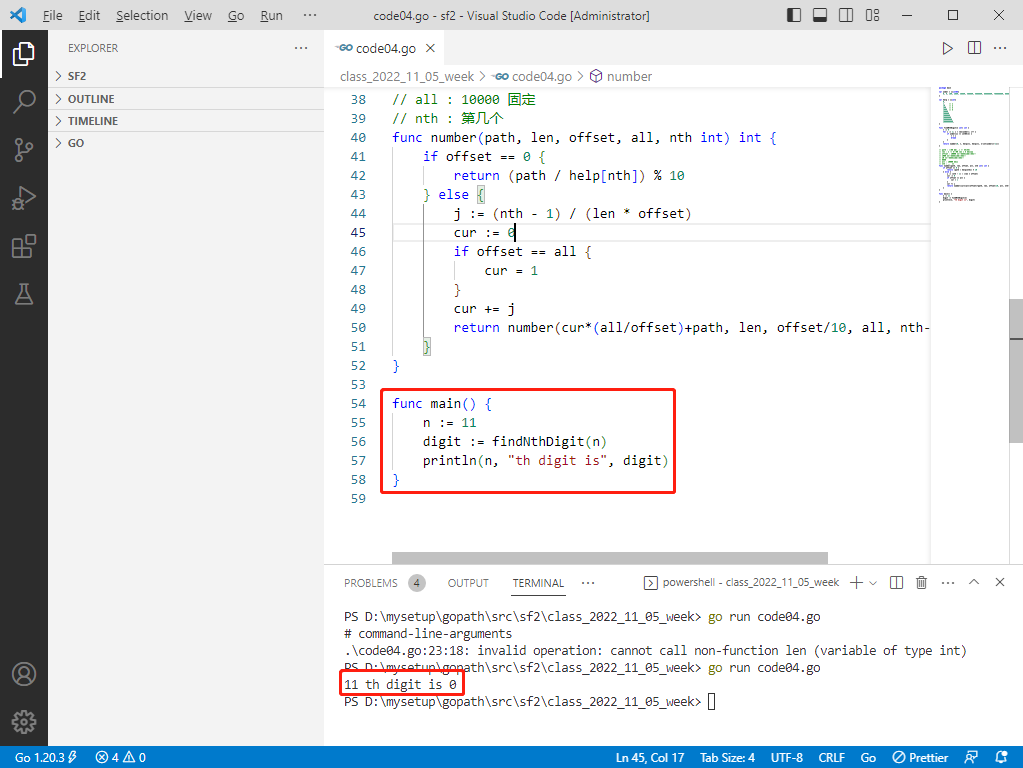
func main() {
n := 11
digit := findNthDigit(n)
println(n, "th digit is", digit)
}
rust完整代码如下:
static mut UNDER: [i64; 11] = [
0,
9,
189,
2889,
38889,
488889,
5888889,
68888889,
788888889,
8888888889,
98888888889,
];
static mut HELP: [i32; 11] = [
0, 1, 10, 100, 1000, 10000, 100000, 1000000, 10000000, 100000000, 1000000000,
];
fn find_nth_digit(n: i32) -> i32 {
let under: &[i64; 11];
let help: &[i32; 11];
unsafe {
under = &UNDER;
help = &HELP;
}
let mut len = 0;
for i in 1..under.len() {
if under[i] >= n as i64 {
len = i;
break;
}
}
number(0, len, help[len], help[len], (n - under[len - 1] as i32))
}
// path : 路径 左(低) <- 右(高)
// len : n -> 5位数 len = 5 固定!
// offset : 10000 目前要决定的是高1位
// 1000 目前要决定的是高2位
// 10 目前要决定的是高2位
// 可变
// all : 10000 固定
// nth : 第几个
fn number(path: i32, len: usize, offset: i32, all: i32, nth: i32) -> i32 {
let help: &[i32; 11];
unsafe {
help = &HELP;
}
if offset == 0 {
return (path / help[nth as usize]) % 10;
} else {
let j = (nth - 1) / (len as i32 * offset);
let cur = if offset == all { 1 } else { 0 } + j;
return number(
cur * (all / offset) + path,
len,
offset / 10,
all,
nth - j * len as i32 * offset,
);
}
}
fn main() {
unsafe {
let n = 11;
let digit = find_nth_digit(n);
println!("{}th digit is {}", n, digit);
}
}

c完整代码如下:
#include <stdio.h>
const long under[] = {
0L, // 0位数,一共能解决几个位
9L, // 1位数,一共能解决几个位
189L, // 1~2位数,一共能解决几个位
2889L, // 1~3位数,一共能解决几个位
38889L,
488889L,
5888889L,
68888889L,
788888889L,
8888888889L,
98888888889L
};
const int help[] = {
0,
1, // 1
10, // 2
100, // 3
1000, // 4
10000,
100000,
1000000,
10000000,
100000000,
1000000000
};
int findNthDigit(int n) {
int len = 0;
for (int i = 1; i < sizeof(under) / sizeof(long); i++) {
if (under[i] >= n) {
len = i;
break;
}
}
return number(0, len, help[len], help[len], n - under[len - 1]);
}
// path : 路径 左(低) <- 右(高)
// len : n -> 5位数 len = 5 固定!
// offset : 10000 目前要决定的是高1位
// 1000 目前要决定的是高2位
// 10 目前要决定的是高2位
// 可变
// all : 10000 固定
// nth : 第几个
int number(int path, int len, int offset, int all, int nth) {
if (offset == 0) {
return (path / help[nth]) % 10;
}
else {
int j = (nth - 1) / (len * offset);
int cur = (offset == all ? 1 : 0) + j;
return number(cur * (all / offset) + path, len, offset / 10, all, nth - j * len * offset);
}
}
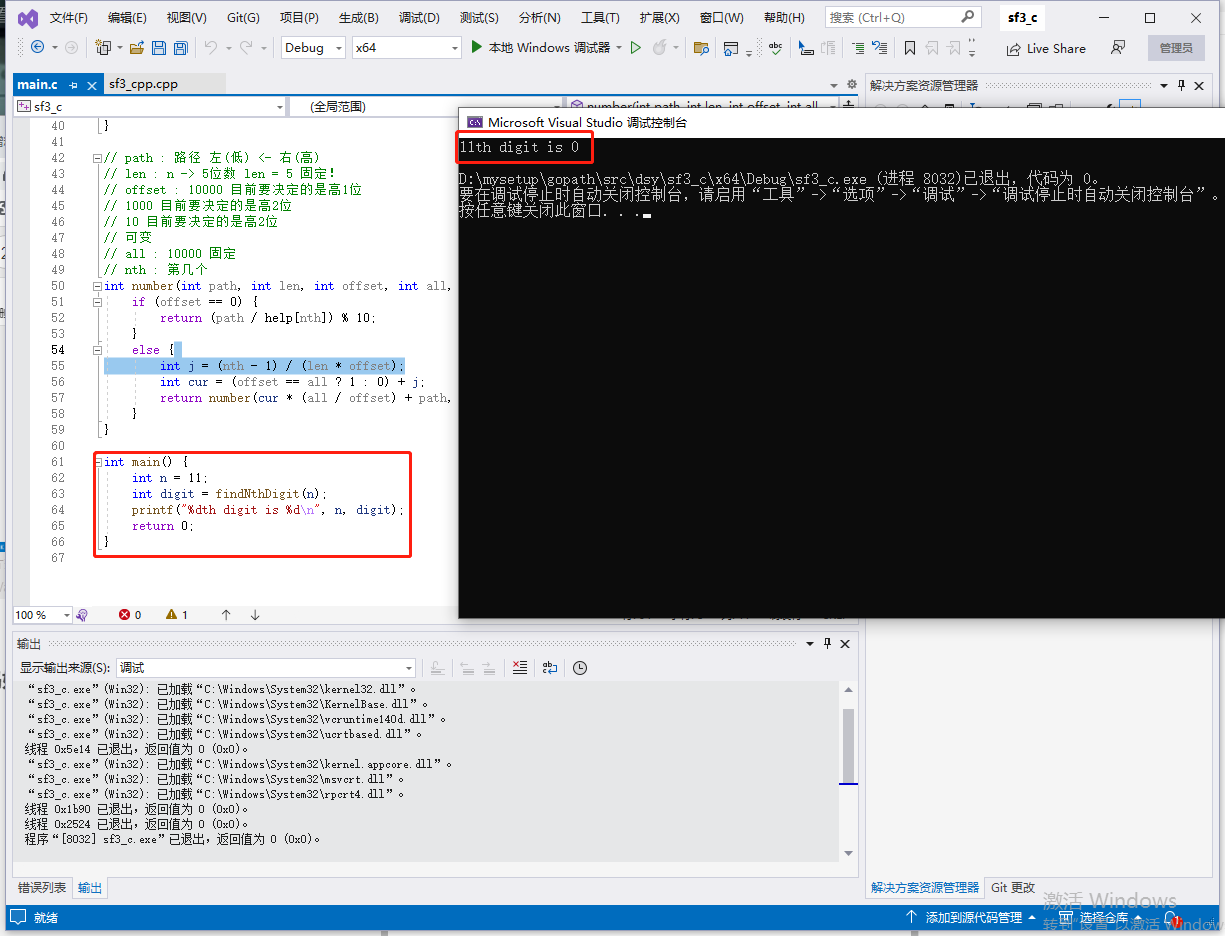
int main() {
int n = 11;
int digit = findNthDigit(n);
printf("%dth digit is %d\n", n, digit);
return 0;
}
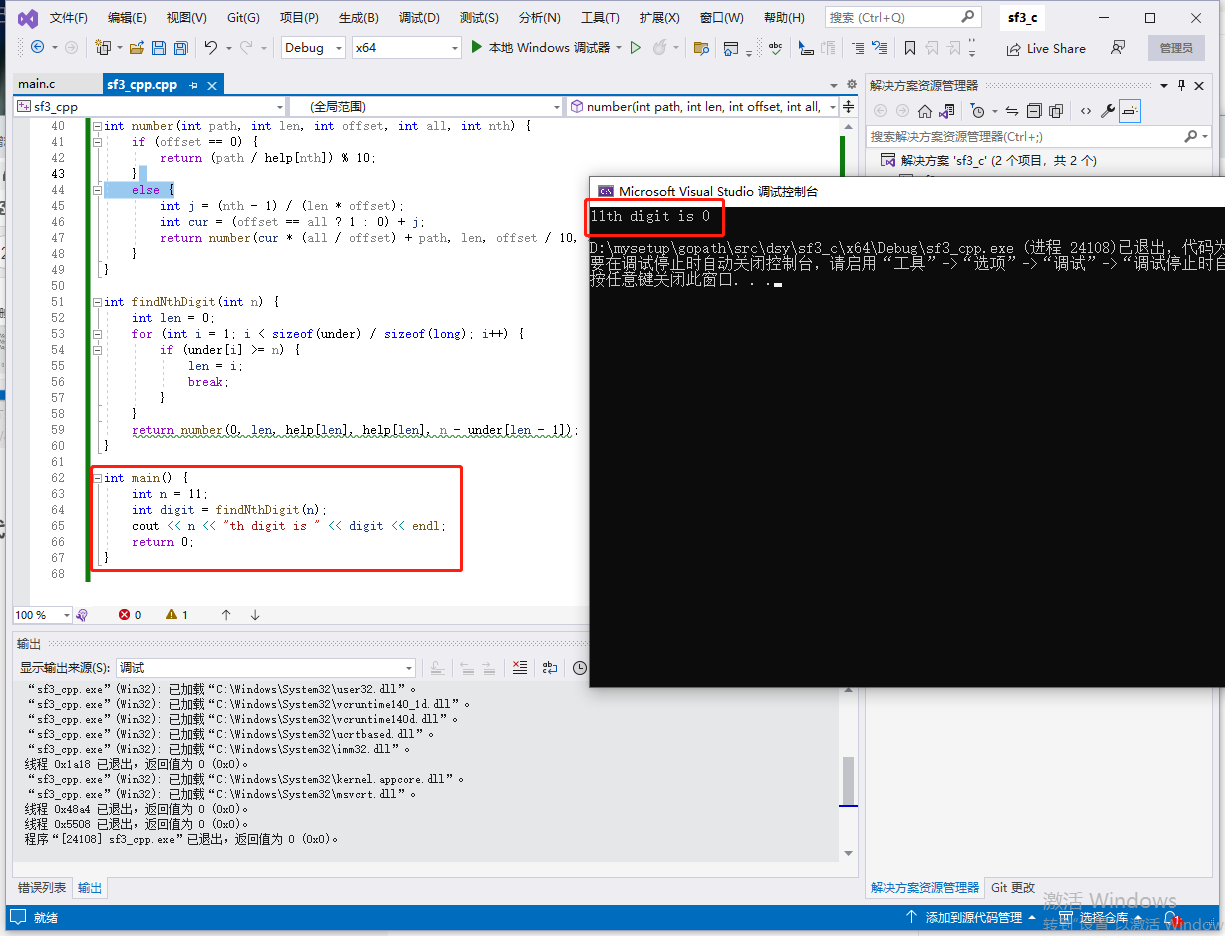
c++完整代码如下:
#include <iostream>
using namespace std;
const long under[] = {
0L, // 0位数,一共能解决几个位
9L, // 1位数,一共能解决几个位
189L, // 1~2位数,一共能解决几个位
2889L, // 1~3位数,一共能解决几个位
38889L,
488889L,
5888889L,
68888889L,
788888889L,
8888888889L,
98888888889L
};
const int help[] = {
0,
1, // 1
10, // 2
100, // 3
1000, // 4
10000,
100000,
1000000,
10000000,
100000000,
1000000000
};
// path : 路径 左(低) <- 右(高)
// len : n -> 5位数 len = 5 固定!
// offset : 10000 目前要决定的是高1位
// 1000 目前要决定的是高2位
// 10 目前要决定的是高2位
// 可变
// all : 10000 固定
// nth : 第几个
int number(int path, int len, int offset, int all, int nth) {
if (offset == 0) {
return (path / help[nth]) % 10;
}
else {
int j = (nth - 1) / (len * offset);
int cur = (offset == all ? 1 : 0) + j;
return number(cur * (all / offset) + path, len, offset / 10, all, nth - j * len * offset);
}
}
int findNthDigit(int n) {
int len = 0;
for (int i = 1; i < sizeof(under) / sizeof(long); i++) {
if (under[i] >= n) {
len = i;
break;
}
}
return number(0, len, help[len], help[len], n - under[len - 1]);
}
int main() {
int n = 11;
int digit = findNthDigit(n);
cout << n << "th digit is " << digit << endl;
return 0;
}