T1 游戏
对于树上三点 \((u,v,w)\) ,一定存在一个点 \(p\) 满足 \(p\to u\) 与 \(p\to v\) 与 \(p\to w\) 的路径两两不重合,考虑枚举 \(p\) 计算答案,由于题目给定 \(\operatorname{dis}(u,v),\operatorname{dis}(u,w),\operatorname{dis}(v,w)\) ,因此我们首先用解方程的方法求解 \(\operatorname{dis}(u,p),\operatorname{dis}(v,p),\operatorname{dis}(w,p)\) ,不妨钦定 \(\operatorname{dis}(u,p)\ge\operatorname{dis}(v,p)\ge\operatorname{dis}(w,p)\) ,预处理每个点为根时最长的三条路径,满足三条路径两两不重合,对于每个点可以得到三元组 \((x,y,z)\) ,此时我们需要找到一个三元组满足 \(\operatorname{dis}(u,p)\le x,\operatorname{dis}(v,p)\le y,\operatorname{dis}(w,p)\le z\) ,经典的三维偏序问题,直接扫描线维护即可。
code
#include <cstdio>
#include <vector>
#include <algorithm>
#include <utility>
using namespace std;
const int max1 = 2e5;
const int inf = 0x3f3f3f3f;
int n, q;
vector <int> edge[max1 + 5];
struct Question
{
int id, x, y, z;
bool operator < ( const Question &A ) const
{ return x > A.x; }
} qus[max1 + 5], tmp[max1 + 5];
int siz[max1 + 5], deep[max1 + 5], father[max1 + 5], son[max1 + 5];
int dfn[max1 + 5], rk[max1 + 5], top[max1 + 5], dfs_clock;
vector < pair <int, int> > f[max1 + 5];
pair <int, int> max_dis[max1 + 5];
int id[max1 + 5], ans[max1 + 5][3];
void Find_Heavy_Edge ( int now, int fa, int depth )
{
siz[now] = 1, deep[now] = depth, father[now] = fa, son[now] = 0;
f[now].clear();
f[now].push_back(make_pair(0, now));
f[now].push_back(make_pair(0, now));
f[now].push_back(make_pair(0, now));
int max_siz = 0;
for ( auto v : edge[now] )
{
if ( v == fa )
continue;
Find_Heavy_Edge(v, now, depth + 1);
if ( siz[v] > max_siz )
max_siz = siz[v], son[now] = v;
siz[now] += siz[v];
f[now].push_back(make_pair(f[v].front().first + 1, f[v].front().second));
sort(f[now].begin(), f[now].end());
reverse(f[now].begin(), f[now].end());
f[now].resize(3);
}
return;
}
void Connect_Heavy_Edge ( int now, int ancestor )
{
top[now] = ancestor;
dfn[now] = ++dfs_clock;
rk[dfs_clock] = now;
if ( son[now] )
Connect_Heavy_Edge(son[now], ancestor);
for ( auto v : edge[now] )
{
if ( v == father[now] || v == son[now] )
continue;
Connect_Heavy_Edge(v, v);
}
return;
}
void Redfs ( int now, int fa )
{
for ( auto v : edge[now] )
{
if ( v == fa )
continue;
max_dis[v] = make_pair(max_dis[now].first + 1, max_dis[now].second);
for ( auto val : f[now] )
{
if ( val.second != -1 && dfn[val.second] >= dfn[v] && dfn[val.second] <= dfn[v] + siz[v] - 1 )
continue;
max_dis[v] = max(max_dis[v], make_pair(val.first + 1, val.second));
}
Redfs(v, now);
}
return;
}
bool Cmp ( const int &x, const int &y )
{
return f[x].front() > f[y].front();
}
struct Segment_Tree
{
#define lson(now) ( now << 1 )
#define rson(now) ( now << 1 | 1 )
pair <int, int> tree[max1 * 4 + 5];
void Build ( int now, int l, int r )
{
tree[now] = make_pair(-inf, -1);
if ( l == r )
return;
int mid = l + r >> 1;
Build(lson(now), l, mid);
Build(rson(now), mid + 1, r);
return;
}
void Insert ( int now, int l, int r, int pos, const pair <int, int> &val )
{
if ( l == r )
{ tree[now] = max(tree[now], val); return; }
int mid = l + r >> 1;
if ( pos <= mid )
Insert(lson(now), l, mid, pos, val);
else
Insert(rson(now), mid + 1, r, pos, val);
tree[now] = max(tree[lson(now)], tree[rson(now)]);
return;
}
pair <int, int> Query ( int now, int l, int r, int ql, int qr )
{
if ( l >= ql && r <= qr )
return tree[now];
int mid = l + r >> 1;
pair <int, int> ans = make_pair(-inf, -1);
if ( ql <= mid )
ans = max(ans, Query(lson(now), l, mid, ql, qr));
if ( qr > mid )
ans = max(ans, Query(rson(now), mid + 1, r, ql, qr));
return ans;
}
}Tree;
int Get_Lca ( int u, int v )
{
while ( top[u] != top[v] )
{
if ( deep[top[u]] < deep[top[v]] )
swap(u, v);
u = father[top[u]];
}
if ( deep[u] > deep[v] )
swap(u, v);
return u;
}
int Get_Dis ( int u, int v )
{
return deep[u] + deep[v] - deep[Get_Lca(u, v)] * 2;
}
int Kth_Ancestor ( int u, int k )
{
while ( deep[u] - deep[top[u]] + 1 <= k )
k -= deep[u] - deep[top[u]] + 1, u = father[top[u]];
return rk[dfn[u] - k];
}
int Get_Point ( int u, int v, int k )
{
int lca = Get_Lca(u, v);
if ( deep[v] - deep[lca] >= k )
return Kth_Ancestor(v, k);
k = deep[u] + deep[v] - deep[lca] - deep[lca] - k;
return Kth_Ancestor(u, k);
}
int main ()
{
freopen("game.in", "r", stdin);
freopen("game.out", "w", stdout);
int sum, d[3], dis[3];
scanf("%d", &n);
for ( int i = 1, u, v; i <= n - 1; i ++ )
scanf("%d%d", &u, &v), edge[u].push_back(v), edge[v].push_back(u);
scanf("%d", &q);
for ( int i = 1; i <= q; i ++ )
{
qus[i].id = i;
scanf("%d%d%d", &qus[i].x, &qus[i].y, &qus[i].z);
sum = qus[i].x + qus[i].y + qus[i].z >> 1;
d[0] = sum - qus[i].x, d[1] = sum - qus[i].y, d[2] = sum - qus[i].z;
sort(d, d + 3);
reverse(d, d + 3);
tmp[i].id = i;
tmp[i].x = d[0], tmp[i].y = d[1], tmp[i].z = d[2];
}
Find_Heavy_Edge(1, 0, 1);
Connect_Heavy_Edge(1, 1);
max_dis[1] = make_pair(-inf, -1);
Redfs(1, 0);
for ( int i = 1; i <= n; i ++ )
{
f[i].push_back(max_dis[i]);
sort(f[i].begin(), f[i].end());
reverse(f[i].begin(), f[i].end());
f[i].resize(3);
id[i] = i;
}
sort(id + 1, id + 1 + n, Cmp);
sort(tmp + 1, tmp + 1 + q);
Tree.Build(1, 0, n);
int now = 1;
for ( int i = 1; i <= q; i ++ )
{
while ( now <= n && f[id[now]].front().first >= tmp[i].x )
{
if ( f[id[now]][1].first >= 0 && f[id[now]][2].first >= 0 )
Tree.Insert(1, 0, n, f[id[now]][1].first, make_pair(f[id[now]][2].first, id[now]));
++now;
}
int k = Tree.Query(1, 0, n, tmp[i].y, n).second;
ans[tmp[i].id][0] = Get_Point(f[k][0].second, k, tmp[i].x);
ans[tmp[i].id][1] = Get_Point(f[k][1].second, k, tmp[i].y);
ans[tmp[i].id][2] = Get_Point(f[k][2].second, k, tmp[i].z);
}
for ( int i = 1; i <= q; i ++ )
{
d[0] = 0, d[1] = 1, d[2] = 2;
do
{
dis[0] = Get_Dis(ans[i][d[0]], ans[i][d[1]]), dis[1] = Get_Dis(ans[i][d[0]], ans[i][d[2]]), dis[2] = Get_Dis(ans[i][d[1]], ans[i][d[2]]);
if ( dis[0] == qus[i].x && dis[1] == qus[i].y && dis[2] == qus[i].z )
{
printf("%d %d %d\n", ans[i][d[0]], ans[i][d[1]], ans[i][d[2]]);
break;
}
} while ( next_permutation(d, d + 3) );
}
return 0;
}
T2 马戏团里你最忙
首先考虑 dp ,设 \(f_{i,s}\) 表示当前考虑了前 \(i\) 个数,第 \(i\) 个数为 \(s\) 时价值的期望,设 \(g_{i,s}\) 表示概率,转移有:
\[\begin{aligned} p(f_{i,s}+g_{i,s}C_{t\operatorname{or}s})&\to f_{i+1,t\operatorname{or}s}\\ (1-p)(f_{i,s}+g_{i,s}C_{t\operatorname{and}s})&\to f_{i+1,t\operatorname{and}s}\\ pg_{i,s}&\to g_{i+1,s\operatorname{or}t}\\ (1-p)g_{i,s}&\to g_{i+1,s\operatorname{and}t} \end{aligned} \]显然转移可以用 FWT 优化。
题解非常神奇的发现 \(f_{i,s}=\sum_{j=1}^m a_jf_{i-j,s}\) ,这满足线性递推,并且 \(m\) 的范围为 \(O(n)\) ,因此我们可以暴力求解 \(f_{i,s}\) 中 \(i\) 的前 \(2m\) 项,建立线性方程组,高斯消元求解 \(a\) ,然后矩阵快速幂即可。
code
#include <cstdio>
#include <algorithm>
#include <iostream>
#include <ctime>
using namespace std;
const int max1 = 17, max2 = 1 << 17;
const int mod = 998244353;
int n, p, k, x0, inv, mid, lim, c[max2 + 5];
int Quick_Power ( int base, int p )
{
int res = 1;
while ( p )
{
if ( p & 1 )
res = 1LL * res * base % mod;
p >>= 1;
base = 1LL * base * base % mod;
}
return res;
}
struct Poly
{ int f[max2 + 5]; };
void FWT_OR ( Poly &A )
{
for ( int i = 0; i < n; i ++ )
for ( int j = 0; j < 1 << i; j ++ )
for ( int k = 0; k < 1 << n; k += 1 << i + 1 )
A.f[1 << i | j | k] = ( 0LL + A.f[1 << i | j | k] + A.f[1 << i | j | k] + A.f[j | k] ) % mod;
return;
}
void FWT_AND ( Poly &A )
{
for ( int i = 0; i < n; i ++ )
for ( int j = 0; j < 1 << i; j ++ )
for ( int k = 0; k < 1 << n; k += 1 << i + 1 )
A.f[j | k] = ( 0LL + A.f[1 << i | j | k] + A.f[j | k] + A.f[j | k] ) % mod;
return;
}
void OR ( const Poly &A, const Poly &B, Poly &C )
{
for ( int s = 0; s < 1 << n; s ++ )
C.f[s] = B.f[s];
FWT_OR(C);
for ( int s = 0; s < 1 << n; s ++ )
C.f[s] = 1LL * C.f[s] * A.f[s] % mod;
return;
}
void AND ( const Poly &A, const Poly &B, Poly &C )
{
for ( int s = 0; s < 1 << n; s ++ )
C.f[s] = B.f[s];
FWT_AND(C);
for ( int s = 0; s < 1 << n; s ++ )
C.f[s] = 1LL * C.f[s] * A.f[s] % mod;
return;
}
Poly A, B, C, D, tmp1, tmp2, tmp3, tmp4, F[75], G[75];
struct Matrix
{
int matrix[75][75];
void Identity ()
{
for ( int i = 1; i <= mid; i ++ )
for ( int j = 1; j <= mid; j ++ )
matrix[i][j] = i == j;
return;
}
Matrix operator * ( const Matrix &A ) const
{
Matrix res;
for ( int i = 1; i <= mid; i ++ )
{
for ( int j = 1; j <= mid; j ++ )
{
res.matrix[i][j] = 0;
for ( int k = 1; k <= mid; k ++ )
res.matrix[i][j] = ( res.matrix[i][j] + 1LL * matrix[i][k] * A.matrix[k][j] ) % mod;
}
}
return res;
}
void Gauss ()
{
int tmp = mid;
for ( int i = 1; i <= mid; i ++ )
{
int pos = i;
for ( int j = i + 1; j <= mid; j ++ )
if ( matrix[j][i] > matrix[pos][i] )
pos = j;
swap(matrix[pos], matrix[i]);
if ( !matrix[i][i] )
{ mid = i - 1; break; }
for ( int j = 1; j <= mid; j ++ )
{
if ( j == i )
continue;
int P = 1LL * matrix[j][i] * Quick_Power(matrix[i][i], mod - 2) % mod;
for ( int w = 1; w <= mid + 1; w ++ )
matrix[j][w] = ( matrix[j][w] - 1LL * matrix[i][w] * P % mod + mod ) % mod;
}
}
for ( int i = 1; i <= mid; i ++ )
matrix[i][i] = 1LL * matrix[i][tmp + 1] * Quick_Power(matrix[i][i], mod - 2) % mod;
lim = mid << 1;
return;
}
}val;
Matrix Quick_Power ( Matrix base, int p )
{
Matrix res;
res.Identity();
while ( p )
{
if ( p & 1 )
res = res * base;
p >>= 1;
base = base * base;
}
return res;
}
int main ()
{
freopen("busy.in", "r", stdin);
freopen("busy.out", "w", stdout);
scanf("%d%d%d%d", &n, &p, &k, &x0);
inv = Quick_Power(1 << n, mod - 2);
for ( int s = 0; s < 1 << n; s ++ )
scanf("%d", &c[s]);
for ( int s = 0; s < 1 << n; s ++ )
{
A.f[s] = 1LL * p * inv % mod;
B.f[s] = 1LL * ( 1 - p + mod ) * inv % mod;
C.f[s] = 1LL * A.f[s] * c[s] % mod;
D.f[s] = 1LL * B.f[s] * c[s] % mod;
F[0].f[s] = 0;
G[0].f[s] = s == x0;
}
mid = 36, lim = mid << 1;
for ( int i = 1; i <= lim; i ++ )
{
OR(A, F[i - 1], tmp1), OR(C, G[i - 1], tmp2), AND(B, F[i - 1], tmp3), AND(D, G[i - 1], tmp4);
for ( int s = 0; s < 1 << n; s ++ )
F[i].f[s] = ( 0LL + tmp1.f[s] + tmp2.f[s] + tmp3.f[s] + tmp4.f[s] ) % mod;
OR(A, G[i - 1], tmp1), AND(B, G[i - 1], tmp2);
for ( int s = 0; s < 1 << n; s ++ )
G[i].f[s] = ( tmp1.f[s] + tmp2.f[s] ) % mod;
}
cerr << "ok1 " << (double)clock() / CLOCKS_PER_SEC << endl;
for ( int i = mid + 1; i <= lim; i ++ )
{
for ( int j = i - 1; j >= i - mid; j -- )
val.matrix[i - mid][i - j] = F[j].f[0];
val.matrix[i - mid][mid + 1] = F[i].f[0];
}
val.Gauss();
for ( int i = 1; i <= mid; i ++ )
val.matrix[1][i] = val.matrix[i][i];
for ( int i = 2; i <= mid; i ++ )
val.matrix[i][i - 1] = 1, val.matrix[i][i] = 0;
cerr << "ok2 " << (double)clock() / CLOCKS_PER_SEC << endl;
val = Quick_Power(val, k - 1);
cerr << "ok3 " << (double)clock() / CLOCKS_PER_SEC << endl;
for ( int s = 0; s < 1 << n; s ++ )
{
int ans = 0;
for ( int i = 1; i <= mid; i ++ )
ans = ( ans + 1LL * val.matrix[mid][i] * F[mid - i + 1].f[s] ) % mod;
printf("%d ", ans);
}
printf("\n");
return 0;
}
T3 树
由于答案设计加法和异或运算,一定难以进行维护,因此我们对位分开进行考虑,首先考虑一条链的情况,设 \(f_{i,j}\) 表示从第 \(i\) 个位置开始向后走 \(2^j\) 步中所有点关于 \(i\) 的距离与点权异或值的和,比较显然转移有:
\[f_{i,j}=f_{i,j-1}+f_{i+2^{j-1},j-1}+\sum_{k=i+2^{j-1}}^{i+2^j-1}2^{j-1}-2^j[v_k第j-1位为1] \]考虑树上的情况,先给一张图:
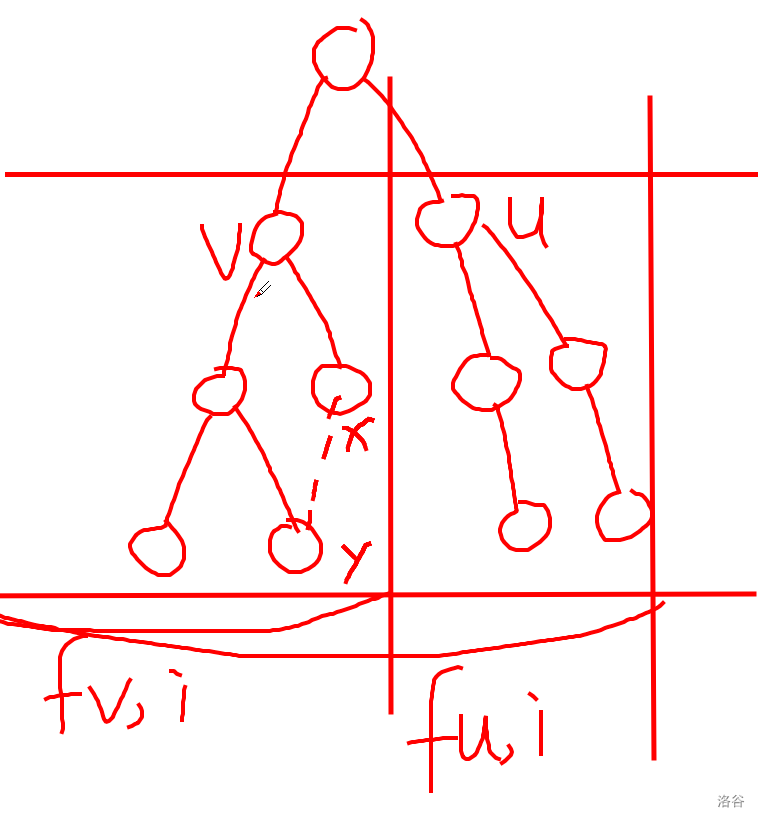
仍然沿用链上求解的思路,设 \(f_{u,i}\) 表示从 \(u\) 节点一直走最靠右的儿子为界,同层的左侧节点的权值之和,此时一次查询显然可以被差分为 \(u\) 的贡献减去 \(v\) 的贡献,特殊的如果一个节点没有右儿子,这个节点的右儿子被定义为如果这个节点有右儿子时,右儿子 bfs 序的上一个节点,例如 \(x\) 的右儿子为 \(y\) ,简单 dp 求解即可。
code
#include <cstdio>
#include <vector>
#include <queue>
#include <iostream>
using namespace std;
const int max1 = 1e6;
int n, q, val[max1 + 5], father[max1 + 5];
vector <int> son[max1 + 5];
queue <int> que;
int bfn[max1 + 5], rk[max1 + 5], bfs_clock, deep[max1 + 5], sum_cnt[20], size[max1 + 5], cnt[max1 + 5][20], Rson[max1 + 5][20];
long long f[max1 + 5][20], sum_val[max1 + 5];
int Get_Rson ( int u, int k )
{
for ( int i = 19; i >= 0; i -- )
if ( ( 1 << i ) <= k && Rson[u][i] )
u = Rson[u][i], k -= 1 << i;
return u;
}
long long Solve ( int u, int k, int R )
{
int t = __lg(k);
long long ans = f[u][t];
if ( k - ( 1 << t ) )
ans += Solve(Rson[u][t], k - ( 1 << t ), R) + ( 1LL << t ) * ( size[Rson[u][t]] - size[Rson[R][0]] ) - ( 1LL << t + 1 ) * ( cnt[Rson[u][t]][t] - cnt[Rson[R][0]][t] );
return ans;
}
int main ()
{
freopen("tree.in", "r", stdin);
freopen("tree.out", "w", stdout);
scanf("%d", &n);
for ( int i = 1; i <= n; i ++ )
scanf("%d", &val[i]);
for ( int i = 2; i <= n; i ++ )
scanf("%d", &father[i]), son[father[i]].push_back(i);
cerr << "ok0 " << (double) clock() / CLOCKS_PER_SEC << endl;
que.push(1);
while ( !que.empty() )
{
int now = que.front();
que.pop();
bfn[now] = ++bfs_clock;
rk[bfs_clock] = now;
int pre = rk[bfn[now] - 1];
deep[now] = deep[father[now]] + 1;
if ( deep[now] != deep[pre] )
for ( int i = 0; i < 20; i ++ )
sum_cnt[i] = 0;
for ( int i = 0; i < 20; i ++ )
sum_cnt[i] += val[now] >> i & 1;
sum_val[deep[now]] += val[now];
size[now] = 1;
if ( deep[now] == deep[pre] )
size[now] += size[pre];
for ( int i = 0; i < 20; i ++ )
cnt[now][i] = sum_cnt[i];
if ( son[now].empty() )
Rson[now][0] = deep[now] == deep[pre] ? Rson[pre][0] : 0;
else
Rson[now][0] = son[now].back();
f[now][0] = sum_val[deep[now]];
for ( auto v : son[now] )
que.push(v);
}
cerr << "ok1 " << (double) clock() / CLOCKS_PER_SEC << endl;
for ( int w = n; w >= 1; w -- )
{
int now = rk[w];
size[now] += size[Rson[now][0]];
for ( int i = 0; i < 20; i ++ )
cnt[now][i] += cnt[Rson[now][0]][i];
}
cerr << "ok1.333" << (double) clock() / CLOCKS_PER_SEC << endl;
for ( int w = n; w >= 1; w -- )
{
int now = rk[w];
for ( int i = 1; Rson[Rson[now][i - 1]][i - 1]; i ++ )
Rson[now][i] = Rson[Rson[now][i - 1]][i - 1];
}
cerr << "ok1.666" << (double) clock() / CLOCKS_PER_SEC << endl;
for ( int w = n; w >= 1; w -- )
{
int now = rk[w];
for ( int i = 1; Rson[father[Rson[now][i - 1]]][i - 1]; i ++ )
f[now][i] = f[now][i - 1] + f[Rson[now][i - 1]][i - 1] + ( 1LL << i - 1 ) * ( size[Rson[now][i - 1]] - size[Rson[now][i]] ) - ( 1LL << i ) * ( cnt[Rson[now][i - 1]][i - 1] - cnt[Rson[now][i]][i - 1] );
}
cerr << "ok2 " << (double) clock() / CLOCKS_PER_SEC << endl;
int u, k, R;
long long ans;
scanf("%d", &q);
while ( q -- )
{
scanf("%d%d", &u, &k);
R = Get_Rson(u, k);
ans = Solve(u, min(k + 1, deep[R] - deep[u] + 1), R);
if ( deep[rk[bfn[u] - 1]] == deep[u] )
{
u = rk[bfn[u] - 1];
R = Get_Rson(u, k);
ans -= Solve(u, min(k + 1, deep[R] - deep[u] + 1), R);
}
printf("%lld\n", ans);
}
cerr << "ok3 " << (double) clock() / CLOCKS_PER_SEC << endl;
return 0;
}