Cards
题意
有 \(N\) 张卡片,每张卡片上都写有两个数字,第 \(i\) 张卡片上的数字分别为 \(P_i, Q_i\)。
同时,\(P = (P_1, P_2, \dots, P_N)\) 和 \(Q = (Q_1, Q_2, \dots, Q_N)\) 都是 \((1, 2, \dots, N)\) 的全排列。
我们需要在 \(N\) 张卡片中选出一些卡片,并且 \(1, 2, \dots, N\) 都出现在至少一张选出的卡片上。
请求出选卡片的方法数,答案对 \(998244353\) 取模。
数据范围
- \(1 \le N \le 2 \times 10^5\)
- \(1 \le P_i, Q_i \le N\),\(P\) 和 \(Q\) 是 \((1, 2, \dots, N)\) 的全排列。
思路
这题需要一定的联想能力。
首先,这些卡牌可以看作构成了一个图,每次将 \(P_i\) 和 \(Q_i\) 连边,可以发现必然会出现环,每个环的方案数就是选择环上的某些边使得环分成的每个连通块的大小都不小于 \(2\) 的方案数。
环与环之间都是独立的,所以要用乘法原理。
问题是,怎样求出每个环的方案数呢?
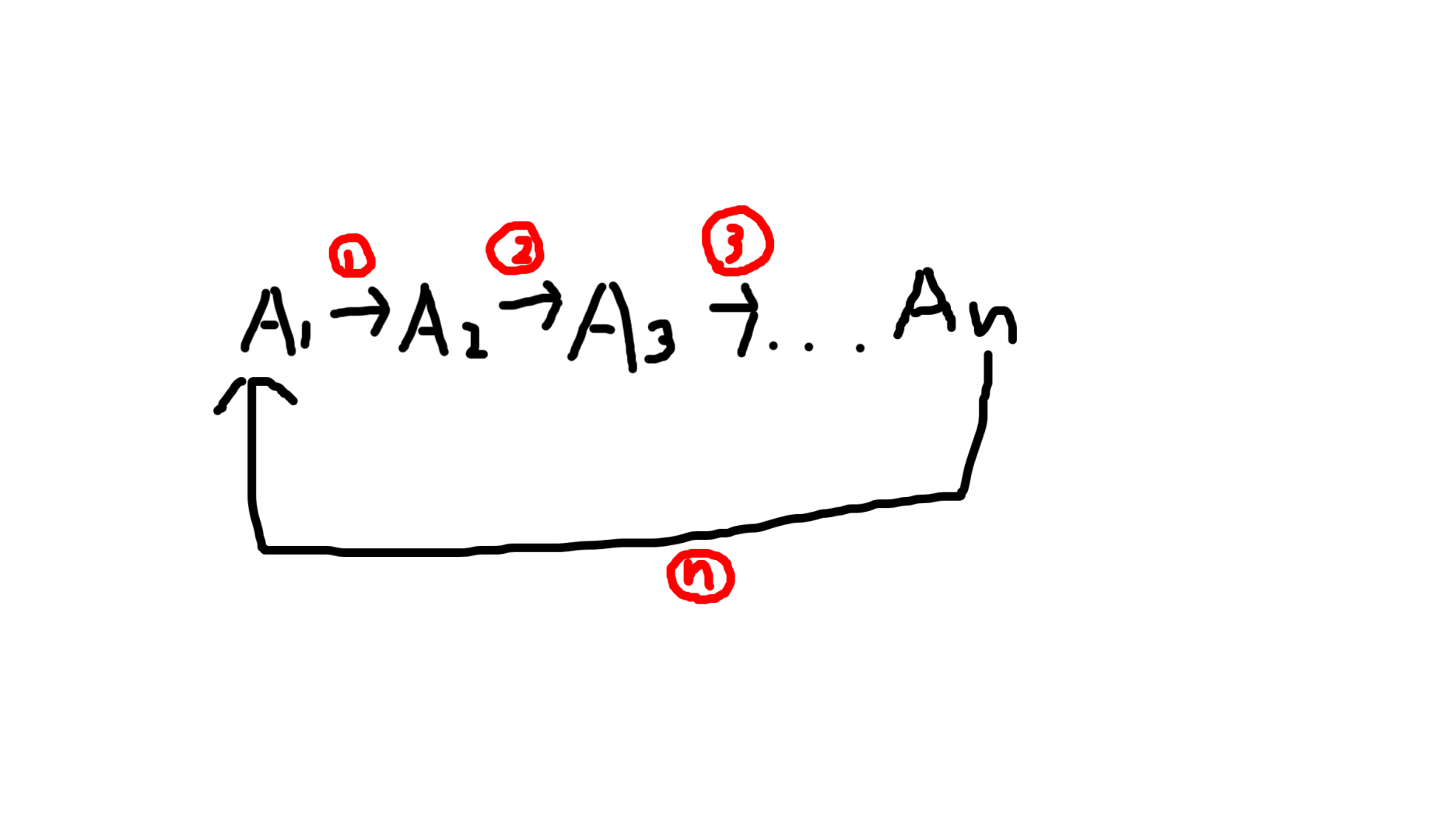
首先,我们有一个小小的环。
然后,我们先来整一个 dp:
- 环的大小为 \(i\),令大小为 \(i\) 的环的方案数为 \(f_i\)。
- \(dp_{i,0}\),边 \(1\) 和边 \(i\) 都不选,不合法。
- \(dp_{i,1}\),选边 \(i\) 而不选边 \(1\),\(dp_{i,1}=dp_{i-1,1}+dp_{i-2,1}\)。
- \(dp_{i,2}\),选边 \(1\) 而不选边 \(i\),\(dp_{i,2}=dp_{i-1,3}\)
- \(dp_{i,3}\),边 \(1\) 和 \(i\) 都选。\(dp_{i,3}=dp_{i-1,3}+dp_{i-2,3}\)
- 那么,\(\color{red}{f_i=dp_{i,1}+dp_{i,2}+dp_{i,3}=dp_{i-1,1}+dp_{i-2,1}+dp_{i-1,3}+dp_{i-1,3}+dp_{i-2,3}=(dp_{i-1,1}+dp_{i-1,3}+dp_{i-1,2})+(dp_{i-2,1}+dp_{i-2,3}+dp_{i-3,3})=f_{i-1}+(dp_{i-2,1}+dp_{i-2,3}+dp_{i-2,2})=f_{i-1}+f_{i-2}}\)(备注:\(dp_{i-2,3}=dp_{i-1,2},dp_{i-3,3}=dp_{i-2,2}\))
- 特别的,通过手推我们发现 \(f_1=1,f_2=3\)。
\(f_i\) 递推一下即可。
复杂度
- 时间:\(O(n)\)
- 空间:\(O(n)\)
Code
点击查看代码
#include <iostream>
using namespace std;
const int N = 2e5 + 10, mod = 998244353;
int n, a[N], b[N], f[N], dp[N];
long long ans = 1;
int dfs (int x) { // 找环
if (f[x]) { // 找到重复点了
return 0;
}
f[x] = 1;
return dfs(b[x]) + 1;
}
int main () {
ios::sync_with_stdio(0), cin.tie(0);
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> a[i];
}
for (int i = 1; i <= n; i++) {
cin >> b[a[i]];
}
dp[1] = 1, dp[2] = 3; // f数组的递推
for (int i = 3; i <= n; i++) {
dp[i] = (dp[i - 1] + dp[i - 2]) % mod; // 记得取模
}
for (int i = 1; i <= n; i++) {
if (!f[i]) {
ans = ans * dp[dfs(i)] % mod; // 乘法原理
}
}
cout << ans;
return 0;
}