标签：结点 struct log2n 链表 二叉树 数据结构 节点

〽️ 数据结构

顺序结构

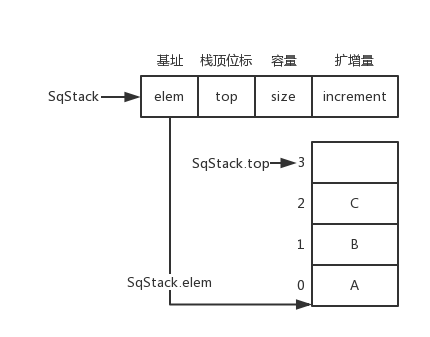
顺序栈（Sequence Stack）

SqStack.cpp

顺序栈数据结构和图片

typedef struct {
	ElemType *elem;
	int top;
	int size;
	int increment;
} SqStack;

队列（Sequence Queue）

队列数据结构

typedef struct {
	ElemType * elem;
	int front;
	int rear;
	int maxSize;
}SqQueue;

非循环队列

非循环队列图片

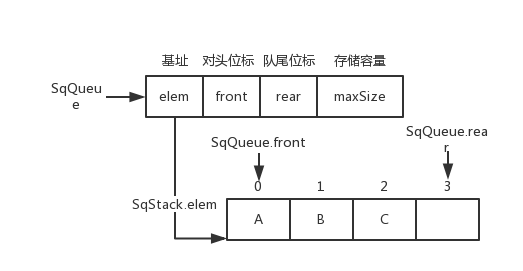
SqQueue.rear++

循环队列

循环队列图片

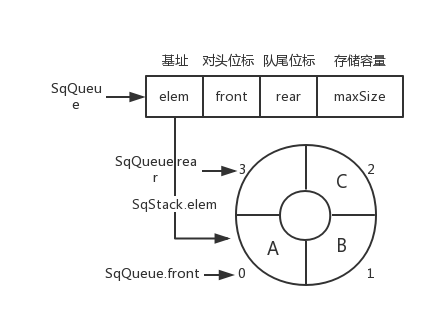
SqQueue.rear = (SqQueue.rear + 1) % SqQueue.maxSize

顺序表（Sequence List）

SqList.cpp

顺序表数据结构和图片

typedef struct {
	ElemType *elem;
	int length;
	int size;
	int increment;
} SqList;

链式结构

LinkList.cpp

LinkList_with_head.cpp

链式数据结构

typedef struct LNode {
    ElemType data;
    struct LNode *next;
} LNode, *LinkList; 

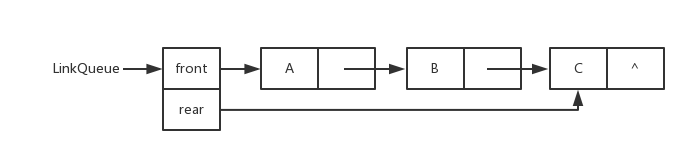
链队列（Link Queue）

链队列图片

线性表的链式表示

单链表（Link List）

单链表图片

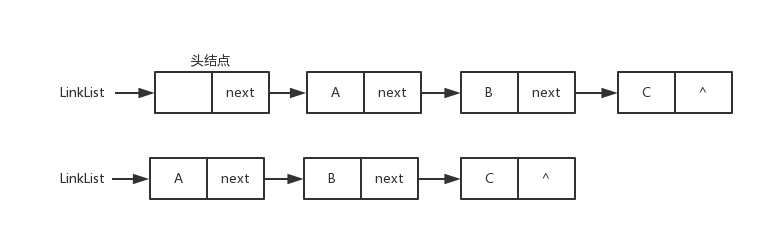
双向链表（Du-Link-List）

双向链表图片

循环链表（Cir-Link-List）

循环链表图片

哈希表

HashTable.cpp

概念

哈希函数：H(key): K -> D , key ∈ K

构造方法

• 直接定址法
• 除留余数法
• 数字分析法
• 折叠法
• 平方取中法

冲突处理方法

• 链地址法：key 相同的用单链表链接
• 开放定址法
  • 线性探测法：key 相同 -> 放到 key 的下一个位置，Hi = (H(key) + i) % m
  • 二次探测法：key 相同 -> 放到 Di = 1^2, -1^2, ..., ±（k)^2,(k<=m/2）
  • 随机探测法：H = (H(key) + 伪随机数) % m

线性探测的哈希表数据结构

线性探测的哈希表数据结构和图片

typedef char KeyType;

typedef struct {
	KeyType key;
}RcdType;

typedef struct {
	RcdType *rcd;
	int size;
	int count;
	bool *tag;
}HashTable;

递归

概念

函数直接或间接地调用自身

递归与分治

• 分治法
  • 问题的分解
  • 问题规模的分解
• 折半查找（递归）
• 归并排序（递归）
• 快速排序（递归）

递归与迭代

• 迭代：反复利用变量旧值推出新值
• 折半查找（迭代）
• 归并排序（迭代）

广义表

头尾链表存储表示

广义表的头尾链表存储表示和图片

// 广义表的头尾链表存储表示
typedef enum {ATOM, LIST} ElemTag;
// ATOM==0：原子，LIST==1：子表
typedef struct GLNode {
    ElemTag tag;
    // 公共部分，用于区分原子结点和表结点
    union {
        // 原子结点和表结点的联合部分
        AtomType atom;
        // atom 是原子结点的值域，AtomType 由用户定义
        struct {
            struct GLNode *hp, *tp;
        } ptr;
        // ptr 是表结点的指针域，prt.hp 和 ptr.tp 分别指向表头和表尾
    } a;
} *GList, GLNode;

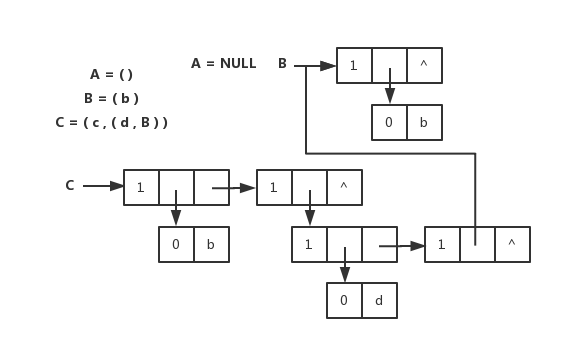
扩展线性链表存储表示

扩展线性链表存储表示和图片

// 广义表的扩展线性链表存储表示
typedef enum {ATOM, LIST} ElemTag;
// ATOM==0：原子，LIST==1：子表
typedef struct GLNode1 {
    ElemTag tag;
    // 公共部分，用于区分原子结点和表结点
    union {
        // 原子结点和表结点的联合部分
        AtomType atom; // 原子结点的值域
        struct GLNode1 *hp; // 表结点的表头指针
    } a;
    struct GLNode1 *tp;
    // 相当于线性链表的 next，指向下一个元素结点
} *GList1, GLNode1;

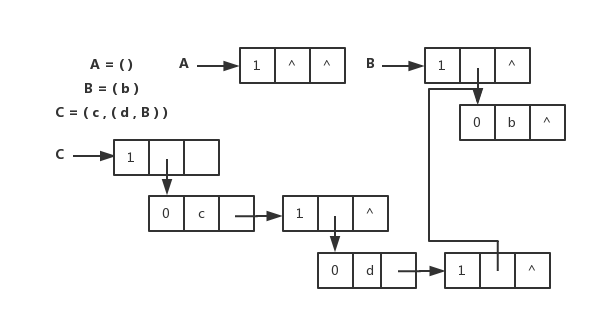
二叉树

BinaryTree.cpp

性质

1. 非空二叉树第 i 层最多 2^(i-1) 个结点 （i >= 1）
2. 深度为 k 的二叉树最多 2^k - 1 个结点 （k >= 1）
3. 度为 0 的结点数为 n₀，度为 2 的结点数为 n₂，则 n₀ = n₂ + 1
4. 有 n 个结点的完全二叉树深度 k = ⌊ log₂(n) ⌋ + 1
5. 对于含 n 个结点的完全二叉树中编号为 i （1 <= i <= n） 的结点
   1. 若 i = 1，为根，否则双亲为 ⌊ i / 2 ⌋
   2. 若 2i > n，则 i 结点没有左孩子，否则孩子编号为 2i
   3. 若 2i + 1 > n，则 i 结点没有右孩子，否则孩子编号为 2i + 1

存储结构

二叉树数据结构

typedef struct BiTNode
{
    TElemType data;
    struct BiTNode *lchild, *rchild;
}BiTNode, *BiTree;

顺序存储

二叉树顺序存储图片

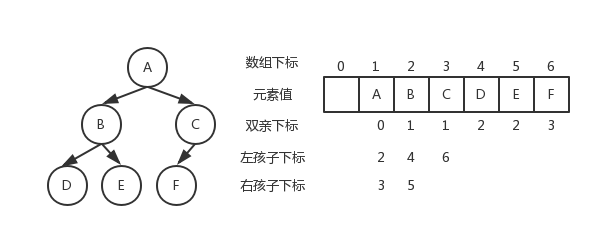
链式存储

二叉树链式存储图片

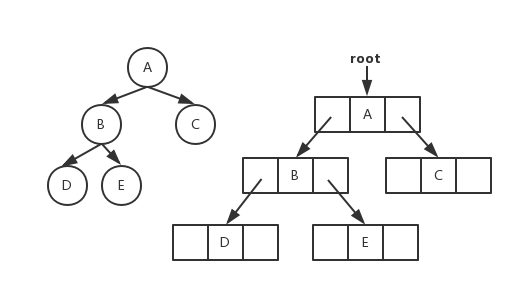
遍历方式

• 先序遍历
• 中序遍历
• 后续遍历
• 层次遍历

分类

• 满二叉树
• 完全二叉树（堆）
  • 大顶堆：根 >= 左 && 根 >= 右
  • 小顶堆：根 <= 左 && 根 <= 右
• 二叉查找树（二叉排序树）：左 < 根 < 右
• 平衡二叉树（AVL树）：| 左子树树高 - 右子树树高 | <= 1
• 最小失衡树：平衡二叉树插入新结点导致失衡的子树：调整：
  • LL型：根的左孩子右旋
  • RR型：根的右孩子左旋
  • LR型：根的左孩子左旋，再右旋
  • RL型：右孩子的左子树，先右旋，再左旋

其他树及森林

树的存储结构

• 双亲表示法
• 双亲孩子表示法
• 孩子兄弟表示法

并查集

一种不相交的子集所构成的集合 S = {S1, S2, ..., Sn}

平衡二叉树（AVL树）

性质

• | 左子树树高 - 右子树树高 | <= 1
• 平衡二叉树必定是二叉搜索树，反之则不一定
• 最小二叉平衡树的节点的公式：F(n)=F(n-1)+F(n-2)+1 （1 是根节点，F(n-1) 是左子树的节点数量，F(n-2) 是右子树的节点数量）

平衡二叉树图片

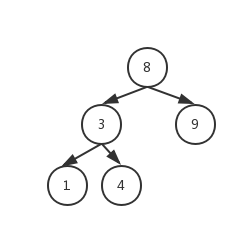
最小失衡树

平衡二叉树插入新结点导致失衡的子树

调整：

• LL 型：根的左孩子右旋
• RR 型：根的右孩子左旋
• LR 型：根的左孩子左旋，再右旋
• RL 型：右孩子的左子树，先右旋，再左旋

红黑树

RedBlackTree.cpp

红黑树的特征是什么？

1. 节点是红色或黑色。
2. 根是黑色。
3. 所有叶子都是黑色（叶子是 NIL 节点）。
4. 每个红色节点必须有两个黑色的子节点。（从每个叶子到根的所有路径上不能有两个连续的红色节点。）（新增节点的父节点必须相同）
5. 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。（新增节点必须为红）

调整

1. 变色
2. 左旋
3. 右旋

应用

• 关联数组：如 STL 中的 map、set

红黑树、B 树、B+ 树的区别？

• 红黑树的深度比较大，而 B 树和 B+ 树的深度则相对要小一些
• B+ 树则将数据都保存在叶子节点，同时通过链表的形式将他们连接在一起。

B 树（B-tree）、B+ 树（B+-tree）

B 树、B+ 树图片

特点

• 一般化的二叉查找树（binary search tree）
• “矮胖”，内部（非叶子）节点可以拥有可变数量的子节点（数量范围预先定义好）

应用

• 大部分文件系统、数据库系统都采用B树、B+树作为索引结构

区别

• B+树中只有叶子节点会带有指向记录的指针（ROWID），而B树则所有节点都带有，在内部节点出现的索引项不会再出现在叶子节点中。
• B+树中所有叶子节点都是通过指针连接在一起，而B树不会。

B树的优点

对于在内部节点的数据，可直接得到，不必根据叶子节点来定位。

B+树的优点

• 非叶子节点不会带上 ROWID，这样，一个块中可以容纳更多的索引项，一是可以降低树的高度。二是一个内部节点可以定位更多的叶子节点。
• 叶子节点之间通过指针来连接，范围扫描将十分简单，而对于B树来说，则需要在叶子节点和内部节点不停的往返移动。

B 树、B+ 树区别来自：differences-between-b-trees-and-b-trees、B树和B+树的区别

八叉树

八叉树图片

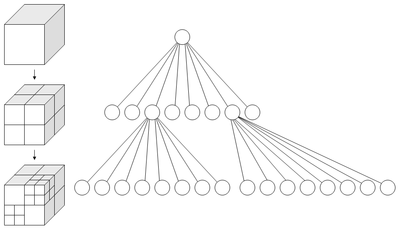
八叉树（octree），或称八元树，是一种用于描述三维空间（划分空间）的树状数据结构。八叉树的每个节点表示一个正方体的体积元素，每个节点有八个子节点，这八个子节点所表示的体积元素加在一起就等于父节点的体积。一般中心点作为节点的分叉中心。

用途

• 三维计算机图形
• 最邻近搜索

⚡️ 算法

排序

排序算法	平均时间复杂度	最差时间复杂度	空间复杂度	数据对象稳定性
冒泡排序	O(n2)	O(n2)	O(1)	稳定
选择排序	O(n2)	O(n2)	O(1)	数组不稳定、链表稳定
插入排序	O(n2)	O(n2)	O(1)	稳定
快速排序	O(n*log2n)	O(n2)	O(log2n)	不稳定
堆排序	O(n*log2n)	O(n*log2n)	O(1)	不稳定
归并排序	O(n*log2n)	O(n*log2n)	O(n)	稳定
希尔排序	O(n*log2n)	O(n2)	O(1)	不稳定
计数排序	O(n+m)	O(n+m)	O(n+m)	稳定
桶排序	O(n)	O(n)	O(m)	稳定
基数排序	O(k*n)	O(n2)		稳定

• 均按从小到大排列
• k：代表数值中的 “数位” 个数
• n：代表数据规模
• m：代表数据的最大值减最小值
• 来自：wikipedia . 排序算法

查找

查找算法	平均时间复杂度	空间复杂度	查找条件
顺序查找	O(n)	O(1)	无序或有序
二分查找（折半查找）	O(log2n)	O(1)	有序
插值查找	O(log2(log2n))	O(1)	有序
斐波那契查找	O(log2n)	O(1)	有序
哈希查找	O(1)	O(n)	无序或有序
二叉查找树（二叉搜索树查找）	O(log2n)
红黑树	O(log2n)
2-3树	O(log2n - log3n)
B树/B+树	O(log2n)

图搜索算法

图搜索算法	数据结构	遍历时间复杂度	空间复杂度
BFS广度优先搜索	邻接矩阵 邻接链表	O(|v|2) O(|v|+|E|)	O(|v|2) O(|v|+|E|)
DFS深度优先搜索	邻接矩阵 邻接链表	O(|v|2) O(|v|+|E|)	O(|v|2) O(|v|+|E|)

其他算法

算法	思想	应用
分治法	把一个复杂的问题分成两个或更多的相同或相似的子问题，直到最后子问题可以简单的直接求解，原问题的解即子问题的解的合并	循环赛日程安排问题、排序算法（快速排序、归并排序）
动态规划	通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法，适用于有重叠子问题和最优子结构性质的问题	背包问题、斐波那契数列
贪心法	一种在每一步选择中都采取在当前状态下最好或最优（即最有利）的选择，从而希望导致结果是最好或最优的算法	旅行推销员问题（最短路径问题）、最小生成树、哈夫曼编码

❓ Problems

Single Problem

• Chessboard Coverage Problem（棋盘覆盖问题）
• Knapsack Problem（背包问题）
• Neumann Neighbor Problem（冯诺依曼邻居问题）
• Round Robin Problem（循环赛日程安排问题）
• Tubing Problem（输油管道问题）

Leetcode Problems

• Github . haoel/leetcode
• Github . pezy/LeetCode

剑指 Offer

• Github . zhedahht/CodingInterviewChinese2
• Github . gatieme/CodingInterviews

Cracking the Coding Interview 程序员面试金典

• Github . careercup/ctci
• 牛客网 . 程序员面试金典

牛客网

• 牛客网 . 在线编程专题

标签：结点,struct,log2n,链表,二叉树,数据结构,节点
From： https://www.cnblogs.com/kennem/p/17298742.html