PAT Basic 1070. 结绳

1. 题目描述：

给定一段一段的绳子，你需要把它们串成一条绳。每次串连的时候，是把两段绳子对折，再如下图所示套接在一起。这样得到的绳子又被当成是另一段绳子，可以再次对折去跟另一段绳子串连。每次串连后，原来两段绳子的长度就会减半。

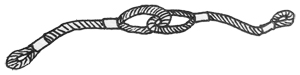
给定 \(N\) 段绳子的长度，你需要找出它们能串成的绳子的最大长度。

2. 输入格式：

每个输入包含 1 个测试用例。每个测试用例第 1 行给出正整数 \(N\) (\(2≤N≤10^4\))；第 2 行给出 \(N\) 个正整数，即原始绳段的长度，数字间以空格分隔。所有整数都不超过\(10^4\)。

3. 输出格式：

在一行中输出能够串成的绳子的最大长度。结果向下取整，即取为不超过最大长度的最近整数。

4. 输入样例：

8
10 15 12 3 4 13 1 15

5. 输出样例：

14

6. 性能要求：

Code Size Limit
16 KB
Time Limit
200 ms
Memory Limit
64 MB

思路：

绳子每串联一次长度就会减半，为了获得最大长度的绳子，较长的绳子应该尽可能少串联，这样损失的长度最少。先把绳子按长度递增排序，然后按照规律计算最终长度即可。

以\(N=5\)为例，假设按长度递增的绳子为\(a,b,c,d,e\)，这里前两根绳子会对折\(N-1\)次，后续绳子的对折次数按顺序从\(N-2\)次递减。这里使用库函数qsort对绳子排序，使用floor进行向下取整。

My Code:

#include <stdio.h>
#include <stdlib.h> // malloc header, qsort header
#include <math.h> // floor header

int cmp(const void *p1, const void *p2);

int main(void)
{
    int ropeCount = 0;
    int *pRope = NULL;
    int i=0;
    double sum = 0.0;
    int res = 0;
    int factor = 0;
    
    scanf("%d", &ropeCount);
    pRope = (int *)malloc(sizeof(int) * ropeCount);
    
    for(i=0; i<ropeCount; ++i)
    {
        scanf("%d", pRope+i);
    }
    qsort(pRope, ropeCount, sizeof(int), cmp); // ascending order
    
    sum += pRope[0] * pow(0.5, ropeCount-1);
    sum += pRope[1] * pow(0.5, ropeCount-1);
    
    factor = ropeCount - 1;
    for(i=2; i<ropeCount; ++i)
    {
        --factor;
        sum += pRope[i] * pow(0.5, factor);
    }
    
    res = floor(sum);
    printf("%d\n", res);
    
//     for(i=0; i<ropeCount; ++i) // test output
//     {
//         printf("%d ", pRope[i]);
//     }
    
    
    free(pRope);
    return 0;
}

int cmp(const void *p1, const void *p2)
{
    return (*(int *)p1 - *(int *)p2);
}