day7

1、530 二叉搜索树中的最小绝对差

1. 思路：

   • 二叉搜索树 ==> 中序遍历 ==> 有序序列

2. 代码

   class Solution {
       private int res = Integer.MAX_VALUE;
       private TreeNode pre;//记录前一个结点
   
       public void traversal(TreeNode node) {
           if(node == null) {
               return;
           }
   
           traversal(node.left);//左
           if(pre != null){//中
               res = Math.min(res, node.val-pre.val);
           }
           pre = node;
           traversal(node.right);//右
   
       }
   
       public int getMinimumDifference(TreeNode root) {
           traversal(root);
           return res;
       }
   }
   

2、501 二叉搜索树中的众数

1. 二叉搜索树 ==> 中序遍历 ==> 有序序列 ==> 比较当前节点和前一节点是否相等，来判断重复节点个数

2. class Solution {
       ArrayList<Integer> resList;
       int count;
       int maxCount;
       TreeNode pre;
   
       public void traversal(TreeNode node) {
           if(node == null) {
               return;
           }
   
           traversal(node.left); //左
   
                                 //中  
           if(pre == null){
               count = 1;
           } else if(pre.val == node.val){
               count++;
           }else{
               count = 1;
           }
           pre = node;
   
           if(count == maxCount){
               resList.add(node.val);
           }
           if(count > maxCount){
               maxCount = count;
               resList.clear();
               resList.add(node.val);
           }
   
           traversal(node.right); //右
   
           return;
       }
   
       public int[] findMode(TreeNode root) {
           resList = new ArrayList<>();
           maxCount = 0;
           count = 0;
           pre = null;
           
           traversal(root);
           int[] res = new int[resList.size()];
           for(int i=0; i<resList.size(); i++){
               res[i] = resList.get(i);
           }
           return res;
       }
   }
   

3、236 二叉树的最近公共祖先

1. 找公共祖先 ==> 从下往上 ==> 后序遍历

2. 递归三部曲

   1. 确定递归函数返回值以及参数

      • 需要递归函数返回值，来告诉我们是否找到节点q或者p
      • 还要返回最近公共节点，可以利用上题目中返回值是 TreeNode，那么如果遇到p或者q，就把q或者p返回，返回值不为空，就说明找到了q或者p。

   2. 确定终止条件

      • 遇到空的话，因为树都是空了，所以返回空。
      • 如果 root == q，或者 root == p，说明找到 q p ，则将其返回，这个返回值，后面在中节点的处理过程中会用到

   3. 确定单层递归逻辑

      • 值得注意的是 本题函数有返回值，是因为回溯的过程需要递归函数的返回值做判断，但本题我们依然要遍历树的所有节点。

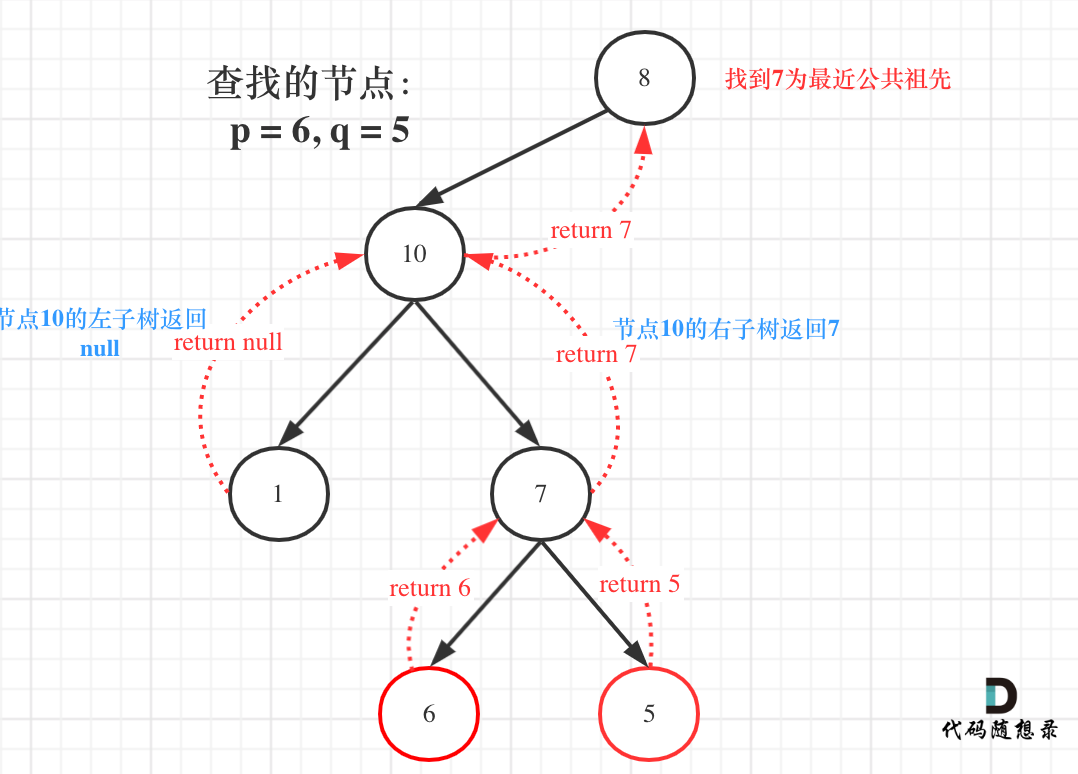
      • 如果left 和 right都不为空，说明此时root就是最近公共节点。

        如果left为空，right不为空，就返回right，说明目标节点是通过right返回的，反之依然。

        

   class Solution {
       public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
           if(root==p || root==q || root==null) {
               return root;
           }
   
           TreeNode left = lowestCommonAncestor(root.left, p, q);//左
           TreeNode right = lowestCommonAncestor(root.right, p, q);//右
   
           if(left!=null && right!=null){//中
               return root;
           } else if(left==null && right!=null){
               return right;
           } else if(left!=null && right==null){
               return left;
           } else {
               return null;
           }
       }
   }