首页 > 其他分享 >块状链表

块状链表

时间：2023-03-25 16:25:49浏览次数：58  
标签：int void ++ 链表 块状 区块 节点

块状链表

基本概念

块状链表本身是一个链表，但是链表储存的并不是一般的数据，而是由这些数据组成的顺序表。每一个块状链表的节点，也就是顺序表，可以被叫做一个块。

块状链表是基于分块思想设计的一种数据结构，其基本定应用为：把一个长度为n的串，分成约块，相邻两块的大小不小于 \(\sqrt n\)，每一块的大小不超过 \(2\sqrt n\)。这样就可以在的时间内解决一个插入、询问、拆分、合并等等的操作。其时间复杂度比平衡树高，空间复杂度比平衡树低。

块状链表就是数组与链表的组合，我们先来回顾一下链表与数组基本操作的时间复杂度：

操作 数组 链表
存储结构 地址连续的存储单元，物理位置相邻 地址不连续，物理位置不相邻
定位 \(O(1)\) \(O(n)\)
插入 \(O(n)\) \(O(1)\)
删除 \(O(n)\) \(O(1)\)

可以发现，数组定位效率较高，但插入删除效率低；链表插入删除效率高，但由于地址不连续，定位效率低。两者各有优缺点。

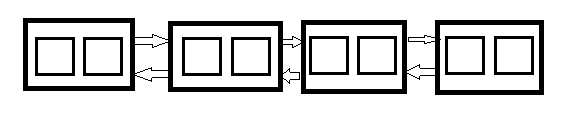
对于一个要求实现定位、插入、删除的数据结构，用平衡树实现过于复杂，我们想办法设计一个兼有数组和链表性质的数据结构，也就是 块状链表。块状链表中的节点是一个个数组，我们将整个序列分为 \(\sqrt n\) 个节点，每个节点数组的大小为 \(\sqrt n\)，这样保证定位和插入删除的复杂度都约为 \(O(\sqrt n)\)。

大概长这个样子：（从csdn上捞的图

实现

一个块状链表至少要支持的操作有 定位、插入、删除 等，在实现过程中，为了维持节点数量，还需要用到 合并 操作，在实现插入、删除过程中会用到 分裂 操作。

实际实现有两种，第一种是把数组作为链表的元素，第二种是把数组分块后每一块都用小链表维护，然后个小链表再用一个大链表串起来。

个人觉得第一种就足够了，不太理解每一块用小链表维护的必要性，下面将以第一种实现为例。如果有的题需要第二种实现可以看这位大佬的博客。

我们以这道题为例讲解一下具体的实现过程。

点击查看题目

[NOI2003] 文本编辑器

题目描述

很久很久以前，\(DOS3.x\) 的程序员们开始对 \(EDLIN\) 感到厌倦。于是，人们开始纷纷改用自己写的文本编辑器⋯⋯

多年之后，出于偶然的机会，小明找到了当时的一个编辑软件。进行了一些简单的测试后，小明惊奇地发现：那个软件每秒能够进行上万次编辑操作（当然，你不能手工进行这样的测试） ！于是，小明废寝忘食地想做一个同样的东西出来。你能帮助他吗？

为了明确目标，小明对“文本编辑器”做了一个抽象的定义:

文本：由 \(0\) 个或多个 ASCII 码在闭区间 [\(32\), \(126\)] 内的字符构成的序列。

光标：在一段文本中用于指示位置的标记，可以位于文本首部，文本尾部或文本的某两个字符之间。

文本编辑器：由一段文本和该文本中的一个光标组成的，支持如下操作的数据结构。如果这段文本为空，我们就说这个文本编辑器是空的。

操作名称 输入文件中的格式 功能
\(\text{Move}(k)\) Move k 将光标移动到第 \(k\) 个字符之后，如果 \(k=0\)，将光标移到文本开头
\(\text{Insert}(n,s)\) Insert n s 在光标处插入长度为 \(n\) 的字符串 \(s\)，光标位置不变\(n\geq1\)
\(\text{Delete}(n)\) Delete n 删除光标后的 \(n\) 个字符，光标位置不变，\(n \geq 1\)
\(\text{Get}(n)\) Get n 输出光标后的 \(n\) 个字符，光标位置不变，\(n \geq 1\)
\(\text{Prev}()\) Prev 光标前移一个字符
\(\text{Next}()\) Next 光标后移一个字符

你的任务是：

  • 建立一个空的文本编辑器。

  • 从输入文件中读入一些操作并执行。

  • 对所有执行过的 GET 操作，将指定的内容写入输出文件。

输入格式

输入文件 editor.in 的第一行是指令条数 \(t\)，以下是需要执行的 \(t\) 个操作。其中：

为了使输入文件便于阅读， Insert 操作的字符串中可能会插入一些回车符， 请忽略掉它们（如果难以理解这句话，可以参照样例） 。

除了回车符之外，输入文件的所有字符的 ASCII 码都在闭区间 [\(32\), \(126\)] 内。且

行尾没有空格。

这里我们有如下假定：

  • MOVE 操作不超过 \(50000\) 个， INSERT 和 DELETE 操作的总个数不超过 \(4000\)，PREV 和 NEXT 操作的总个数不超过 \(200000\)。

  • 所有 INSERT 插入的字符数之和不超过 \(2M\)（\(1M=1024\times 1024\) 字节） ，正确的输出文件长度不超过 \(3M\) 字节。

  • DELETE 操作和 GET 操作执行时光标后必然有足够的字符。 MOVE 、 PREV 、 NEXT 操作必然不会试图把光标移动到非法位置。

  • 输入文件没有错误。

对 C++ 选手的提示：经测试，最大的测试数据使用 fstream 进行输入有可能会比使用 stdio 慢约 \(1\) 秒。

输出格式

输出文件 editor.out 的每行依次对应输入文件中每条 Get 指令的输出。

样例 #1

样例输入 #1

15
Insert 26
abcdefghijklmnop
qrstuv wxy
Move 15
Delete 11
Move 5
Insert 1
^
Next
Insert 1
_
Next
Next
Insert 4
.\/.
Get 4
Prev
Insert 1
^
Move 0
Get 22

样例输出 #1

.\/.
abcde^_^f.\/.ghijklmno

构建

定义一个结构体，储存数组、数组大小、左节点、右节点等信息。

struct node {
    char s[2005];
    int c, l, r;
}p[maxn];

这道题没有给定初始数组，如果给定了初始数组，可以先将初始数组加入链表。

定位

在这道题中相当于 Move 操作。假设我们要定位到 \(k\)，那么我们可以利用保存的节点大小找到这个位置在的那一块，然后根据数组下标定位。故而可以将 \(k\) 的“坐标”设为 \((x, y)\)，用来表示在哪个节点的哪个位置。

void move(int k) {
    x = p[0].r;
    while (k > p[x].c) k -= p[x].c, x = p[x].r;
    y = k - 1;
}

对于 Prev 操作和 Next 操作，只需判断是否在块内的情况即可。

void pre() {
    if (!y) x = p[x].l, y = p[x].c - 1;
    else y--;
}

void nxt() {
    if (y < p[x].c - 1) y++;
    else x = p[x].r, y = 0;
}

插入

分为两种情况。

添加区间在两个块之间

对于插入的区间新建区块存储（可能是多个），然后接到原链表上。

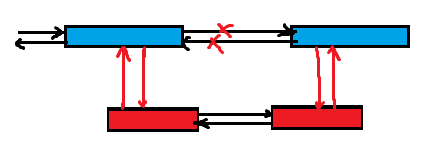
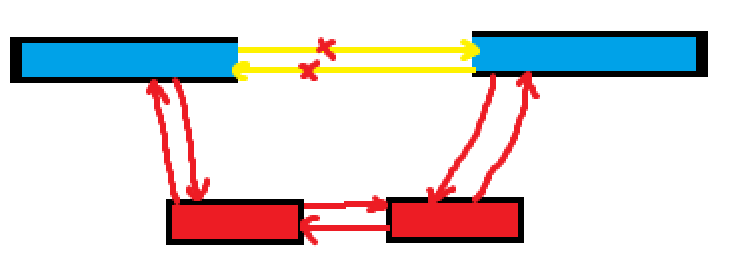
添加区间在一个块内

首先要将所要插入到的那个区块从插入位置断开：

然后就是和第一种情况一样地，将待插入区间新建区块，插入原链表

再看具体实现，对于断区间的操作，我们可以新建一个节点，复制断点后的全部信息，再在原先节点删去断点后的信息，时间复杂度 \(O(\sqrt n)\)；对于将新区间插入的操作，每 \(\sqrt n\) 长度新建一个区块，最坏情况要新建 \(\sqrt n\) 个区块，时间复杂度也是 \(O(\sqrt n)\)。

Code：

//insert k ch
void insert(int k) {
    //cur in node -->split
    if (y < p[x].c - 1) {
        int u = q[tot--];
        for (int i = y + 1; i < p[x].c; i++) 
            p[u].s[p[u].c++] = p[x].s[i];
        p[x].c = y + 1;
        add(x, u);
    }
    //creat and insert new nodes
    int cur = x;
    for (int i = 0; i < k;) {
        int u = q[tot--];
        while (p[u].c < 2005 && i < k)
            p[u].s[p[u].c++] = str[i++];
        add(cur, u);
        cur = u;
    }
}

其中，对于 \(add\) 函数：

//add v to u's right
void add(int u, int v) {
    p[v].r = p[u].r, p[p[v].r].l = v;
    p[u].r = v, p[v].l = u;
}

删除

依旧是分为两种情况：

删除区间在一个区块内

这种情况好说，只需动一动这个区块的数组下标和元素个数总数就行了。

if (p[x].c - 1 - y >= k) {
    for (int i = y + k + 1, j = y + 1; i < p[x].c; i++, j++) 
        p[x].s[j] = p[x].s[i];
    p[x].c -= k;
}

删除区间跨越区块

需要分别删除开头区块的后半段区间、结尾区块的前半段区间和中间的整块节点。前两个好说，方法同第一种情况，下面主要说整块节点的删除。

我们回想一下之前链表删除节点，就是断绝被删节点与周围节点的关系：

对于块状链表的节点，我们显然也可以这么办。但是有一个新的问题产生了：对于我们删掉的节点，它的节点编号是被永远占用的，换句话说，它永远要占一部分内存，这就有可能在添加区间时增加的节点无处可放，超出内存限制。

所以我们要用到一种 内存回收 的技巧来优化。也就是上文插入操作的代码中的 \(q\) 数组和 \(tot\)。我们在一开始就先将 \(q(i)\) 初始为 \(i\)，\(tot\) 初始为 最大节点数量，相当于是构建了一个栈，在增加节点时就去除栈顶元素作为编号，在删除节点时就将其编号重新放入栈中表示已经没有有用信息使用这个节点了，可以占用这个编号。这也体现了链表存储的非连续性。

Code：

void delet(int u) {
    p[p[u].l].r = p[u].r;
    p[p[u].r].l = p[u].l;
    p[u].l = p[u].r = p[u].c = 0;
    q[++tot] = u;  //内存回收
}

void remove(int k) {
    if (p[x].c - 1 - y >= k) {
        for (int i = y + k + 1, j = y + 1; i < p[x].c; i++, j++) 
            p[x].s[j] = p[x].s[i];
        p[x].c -= k;
    }
    else {
        k -= p[x].c - y - 1;
        p[x].c = y + 1;
        while (p[x].r && k >= p[p[x].r].c) {
            int u = p[x].r;
            k -= p[u].c;
            delet(u);
        }
        int u = p[x].r;
        for (int i = 0, j = k; j < p[u].c; i++, j++) 
            p[u].s[i] = p[u].s[j];
        p[u].c -= k;
    }
}

合并——保持平衡

如同平衡树的旋转一样，块状链表的合并也是保持“平衡”的一种手段。块状链表实际上就是将数组与链表结合，达到定位与插入删除的平衡，合并操作也是在维护这种平衡。

在上文提到的插入操作和删除操作中，可能会产生许多区块长度远小于 \(\sqrt n\) 的区块，这会大大降低块状链表的效率。所以我们在一定频率内，扫描一次整个链表，如果发现有相邻两个区块长度加起来还小于 \(\sqrt n\)，就将它们合并为一个区块。时间复杂度约 \(O(\sqrt n)\)。

void merge() {
    for (int i = p[0].r; i; i = p[i].r) {
        while (p[i].r && p[i].c + p[p[i].r].c < 2005) {
            int r = p[i].r;
            for (int j = p[i].c, k = 0; k < p[r].c; j++, k++) 
                p[i].s[j] = p[r].s[k];
            if (x == r) x = i, y += p[i].c;
            p[i].c += p[r].c;
            delet(r);
        }
    }
}

查询

查询操作其实就很简单了~依旧是分在一个区块和多个区块两种情况。

void get(int k) {
    if (p[x].c - 1 - y >= k)  {
        for (int i = 0, j = y + 1; i < k; i++, j++) 
            cout << p[x].s[j];
    }
    else {
        k -= p[x].c - y - 1;
        for (int i = y + 1; i < p[x].c; i++) 
            cout << p[x].s[i];
        int cur = x;
        while (p[cur].r && k >= p[p[cur].r].c) {
            int u = p[cur].r;
            for (int i = 0; i < p[u].c; i++) cout << p[u].s[i];
            k -= p[u].c;
            cur = u;
        }
        int u = p[cur].r;
        for (int i = 0; i < k; i ++ ) cout << p[u].s[i];
    }
    cout << endl;
}
点击查看代码 
#include <bits/stdc++.h>
#define maxn 100005
using namespace std;
inline int read() {
    int x = 0, f = 1; char c = getchar();
    while (c < '0' || c > '9') { if (c == '-') f = -1; c = getchar(); }
    while (c >= '0' && c <= '9') { x = x * 10 + c - '0'; c = getchar(); }
    return x * f;
}
struct node {
    char s[2005];
    int c, l, r;
    // 一个块 ：0~c
}p[2005];
char str[2000005];
int q[2005], tot;
int n, x, y; // x: 第几个节点 y: 节点中第几个位置

void move(int k) {
    x = p[0].r;
    while (k > p[x].c) k -= p[x].c, x = p[x].r;
    y = k - 1;
}

void pre() {
    if (!y) x = p[x].l, y = p[x].c - 1;
    else y--;
}

void nxt() {
    if (y < p[x].c - 1) y++;
    else x = p[x].r, y = 0;
}

//add v to u's right
void add(int u, int v) {
    p[v].r = p[u].r, p[p[v].r].l = v;
    p[u].r = v, p[v].l = u;
}

void delet(int u) {
    p[p[u].l].r = p[u].r;
    p[p[u].r].l = p[u].l;
    p[u].l = p[u].r = p[u].c = 0;
    q[++tot] = u;  //内存回收
}

//insert k ch
void insert(int k) {
    //cur in node -->split
    if (y < p[x].c - 1) {
        int u = q[tot--];
        for (int i = y + 1; i < p[x].c; i++) 
            p[u].s[p[u].c++] = p[x].s[i];
        p[x].c = y + 1;
        add(x, u);
    }
    //creat and insert new nodes
    int cur = x;
    for (int i = 0; i < k;) {
        int u = q[tot--];
        while (p[u].c < 2005 && i < k)
            p[u].s[p[u].c++] = str[i++];
        add(cur, u);
        cur = u;
    }
}

void remove(int k) {
    if (p[x].c - 1 - y >= k) {
        for (int i = y + k + 1, j = y + 1; i < p[x].c; i++, j++) 
            p[x].s[j] = p[x].s[i];
        p[x].c -= k;
    }
    else {
        k -= p[x].c - y - 1;
        p[x].c = y + 1;
        while (p[x].r && k >= p[p[x].r].c) {
            int u = p[x].r;
            k -= p[u].c;
            delet(u);
        }
        int u = p[x].r;
        for (int i = 0, j = k; j < p[u].c; i++, j++) 
            p[u].s[i] = p[u].s[j];
        p[u].c -= k;
    }
}

void get(int k) {
    if (p[x].c - 1 - y >= k)  {
        for (int i = 0, j = y + 1; i < k; i++, j++) 
            cout << p[x].s[j];
    }
    else {
        k -= p[x].c - y - 1;
        for (int i = y + 1; i < p[x].c; i++) 
            cout << p[x].s[i];
        int cur = x;
        while (p[cur].r && k >= p[p[cur].r].c) {
            int u = p[cur].r;
            for (int i = 0; i < p[u].c; i++) cout << p[u].s[i];
            k -= p[u].c;
            cur = u;
        }
        int u = p[cur].r;
        for (int i = 0; i < k; i ++ ) cout << p[u].s[i];
    }
    cout << endl;
}

void merge() {
    for (int i = p[0].r; i; i = p[i].r) {
        while (p[i].r && p[i].c + p[p[i].r].c < 2005) {
            int r = p[i].r;
            for (int j = p[i].c, k = 0; k < p[r].c; j++, k++) 
                p[i].s[j] = p[r].s[k];
            if (x == r) x = i, y += p[i].c;
            p[i].c += p[r].c;
            delet(r);
        }
    }
}
signed main() {
    for (int i = 1; i < 2005; i++) q[++tot] = i;
    n = read();
    char opt[15];
    str[0] = '%';
    insert(1); move(1);
    while (n--) {
        cin >> opt;
        if (!strcmp(opt, "Move")) {
            int a = read();
            move(a + 1);
        }
        if (!strcmp(opt, "Insert")) {
            // int k = read();
            // for (int i = 0; i < k;) {
            //     cin >> str[i];
            //     if (str[i] >= 32 && str[i] <= 126) i++;
            // }
            int a;
            scanf("%d", &a);
            int i = 0, k = a;
            while (a)
            {
                str[i] = getchar();
                if (str[i] >= 32 && str[i] <= 126) i ++, a -- ;
            }
            insert(k);
            merge();
        }
        if (!strcmp(opt, "Delete")) {
            int a = read();
            remove(a);
            merge();
        }
        if (!strcmp(opt, "Get")) {
            int a = read();
            get(a);
        }
        if (!strcmp(opt, "Prev")) pre();
        if (!strcmp(opt, "Next")) nxt();
    }
}

标签：int,void,++,链表,块状,区块,节点
From： https://www.cnblogs.com/djc01/p/17254947.html

相关文章

  • 链表中环的入口结点
    方法1，遍历一次，使用额外空间哈希直接存储指针出现的次数，如果重复出现，直接返回即可classSolution{public:unordered_map<ListNode*,int>hashmap;//记录指针及其......
  • 快慢指针-lc876链表的中间节点
    给你单链表的头结点head，请你找出并返回链表的中间结点。如果有两个中间结点，则返回第二个中间结点。示例1：输入：head=[1,2,3,4,5]输出：[3,4,5]解释：链表只有一个中间......
  • 数据结构-->单链表OJ题--->讲解_02
    老铁们，本期讲解反转单链表双指针法代码如下所示:>现在附上测试环节:>以及最终实现的图样链表，如下：另外，别忘了对“Reverse_SLT”反转函数于头文件中声明！！这就是采用双指针......
  • 指针与链表
    指针与链表各位CTFer可以忽略这篇文章~各位CTFer可以忽略这篇文章~各位CTFer可以忽略这篇文章~指针指针的定义指针对于变量来讲就像单人间的宿舍号一样。每个人(变量......
  • 数据结构-->单链表OJ题--->讲解_01
    老铁们，本期我们开讲单链表OJ题的讲解：删除单链表中给定的val值，并将剩余的链表进行链接本题中val的值是11，删除后的图示链接为:>显然，我们需要指针cur移动来寻找指定数值val......
  • 【leetcode-链表】两两交换链表中的节点
    题目：给定一个链表，两两交换其中相邻的节点，并返回交换后的链表。你不能只是单纯的改变节点内部的值，而是需要实际的进行节点交换。 示例:1->2->3->42->1->4->3思路：首先需要建......
  • 141.环形链表
    给你一个链表的头节点head，判断链表中是否有环。如果链表中有某个节点，可以通过连续跟踪next指针再次到达，则链表中存在环。为了表示给定链表中的环，评测系统内部使用整......
  • JZ6 从尾到头打印链表
      链表是存储数据的一种方式，由于内存不是连续的，因此访问只能从表头访问表尾。本题需要从尾部到头打印链表，只能借助特殊的数据结构输出，但是访问顺序不会因此改变。首先......
  • 论单向链表有序插入方案
    0.思考单向链表有序插入，插入点分为这样几个地方：当前链表为空，被插入节点是第一个节点被插入节点作为头结点被插入节点在中间被插入节点在尾部那么按照这样的步骤一......
  • 单链表OJ题解析1
    1.移除链表元素题目链接题目描述 解题思路这道题较好的解法是创建一个新链表,把不等于val的节点链接到一起,然后返回新链表的头结点structListNode*removeEle......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99