哈夫曼编码(\(Huffman\) \(Coding\))原理详解
一、哈夫曼编码简介
哈夫曼编码,又称为霍夫曼编码(\(Huffman\) \(Coding\))
是一种可变长编码(\(VLC\), \(variable\) \(length\) \(coding\))方式,比起定长编码的 \(ASCII\) 编码来说,哈夫曼编码能节省很多的空间,因为每一个字符出现的频率不是一致的;
是一种用于无损数据压缩的熵编码算法,通常用于压缩重复率比较高的字符数据。
如果我们通过转换成\(ASCII\)码对应的二进制数据将字符串 \(BCAADDDCCACACAC\) 通过二进制编码进行传输,那么一个字符传输的二进制位数为 \(8bits\),那么总共需要 \(120\) 个二进制位;而如果使用哈夫曼编码,该串字符可压缩至\(28\)位。

二、哈夫曼编码方法
哈夫曼编码首先会使用字符的频率创建一棵树,然后通过这个树的结构为每个字符生成一个特定的编码,出现频率高的字符使用较短的编码,出现频率低的则使用较长的编码,这样就会使编码之后的字符串平均长度降低,从而达到数据无损压缩的目的。
1. 计算字符串中每个字符的频率:

2. 按照字符出现的频率进行排序,组成一个队列 \(Q\)
出现频率最低的在前面,出现频率高的在后面。

3. 把这些字符作为叶子节点开始构建一颗哈夫曼树
哈夫曼树又称为最优二叉树,是一种带权路径长度最短的二叉树。
- 首先创建一个空节点 \(z\),将最小频率的字符分配给 \(z\) 的左侧,并将频率排在第二位的分配给 \(z\) 的右侧,然后将 \(z\) 赋值为两个字符频率的和;然后从队列 \(Q\) 中删除 \(B\) 和 \(D\),并将它们的和添加到队列中,上图中 \(*\) 表示的位置。
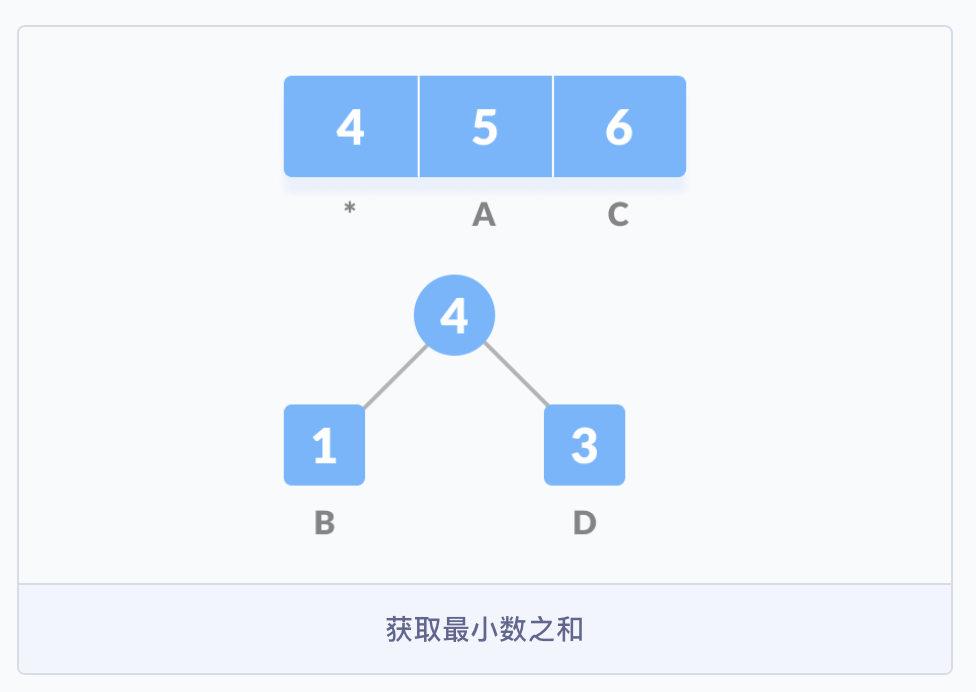
- 紧接着,重新创建一个空的节点 \(z\),并将 \(4\) 作为左侧的节点,频率为 \(5\) 的 \(A\) 作为右侧的节点,\(4\) 与 \(5\) 的和作为父节点,并把这个和按序加入到队列中,再根据频率从小到大构建树结构(小的在左)。
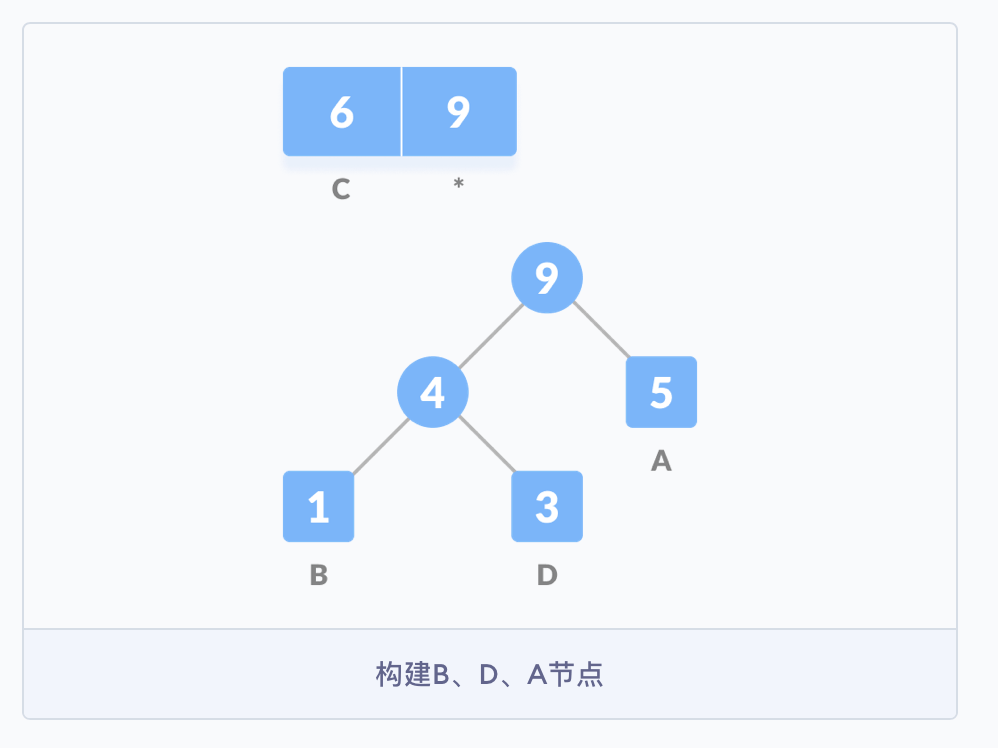
- 继续按照之前的思路构建树,直到所有的字符都出现在树的节点中,哈夫曼树构建完成。
节点的带权路径长度:为从根节点到该节点的路径长度与节点权值的乘积。
该二叉树的带权路径长度 \(WPL = 6 * 1 + 5 * 2 + 3 * 3 + 1 * 3 = 28\)
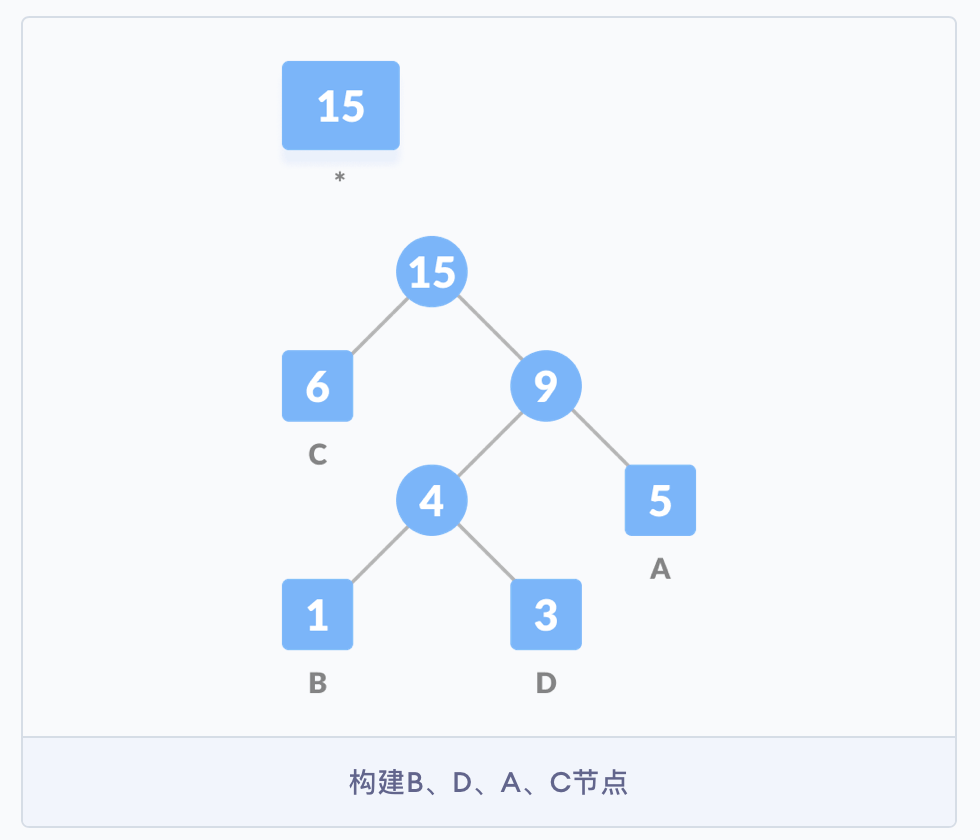
-
- 对字符进行编码
哈夫曼树构建完成,下面我们要对各个字母进行编码,
编码原则:对于每个非叶子节点,将 \(0\) 分配给连接线的左侧,\(1\) 分配给连接线的右侧,最终得到字符的编码就是从根节点开始,到该节点的路径上的 \(01\) 序列组合。
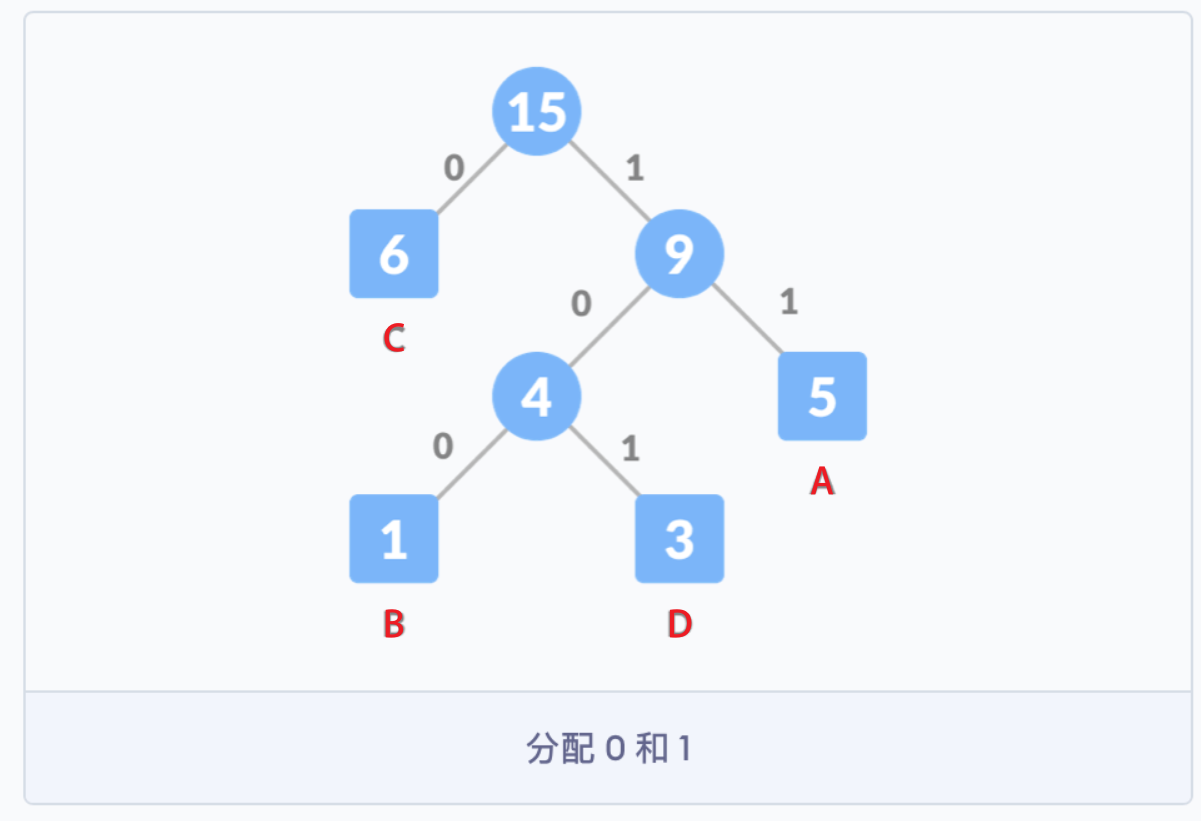
因此各个字母的编码分别为:
| \(A\) | \(B\) | \(C\) | \(D\) |
|---|---|---|---|
| \(11\) | \(100\) | \(0\) | \(101\) |
在没有经过哈夫曼编码之前,字符串\(\large BCAADDDCCACACAC\)的二进制为:
10000100100001101000001010000010100010001000100010001000100001101000011010000010100001101000001010000110100000101000011
也就是占了 \(120\) 比特;
编码之后为:
1000111110110110100110110110
占了 \(28\) 比特。
5. 确定发送的数据
哈夫曼编码将发送字符串的数据长度极大压缩,考虑到接收方的编码,还需要把哈夫曼树的结构也传递过去。
即字符占用的 \(32\) 比特和 频率占用的 \(15\) 比特也需要传递过去。
总体上,编码后比特数为\(32 + 15 + 28 = 75\),比 \(120\) 比特少了 \(45\) 个,效率还是非常高的。
注:之所以把字符和频率再发过去,对方就知道\(A:11\),\(B:1001\)...,以此来对\(ABCD\)进行相应的解码工作。
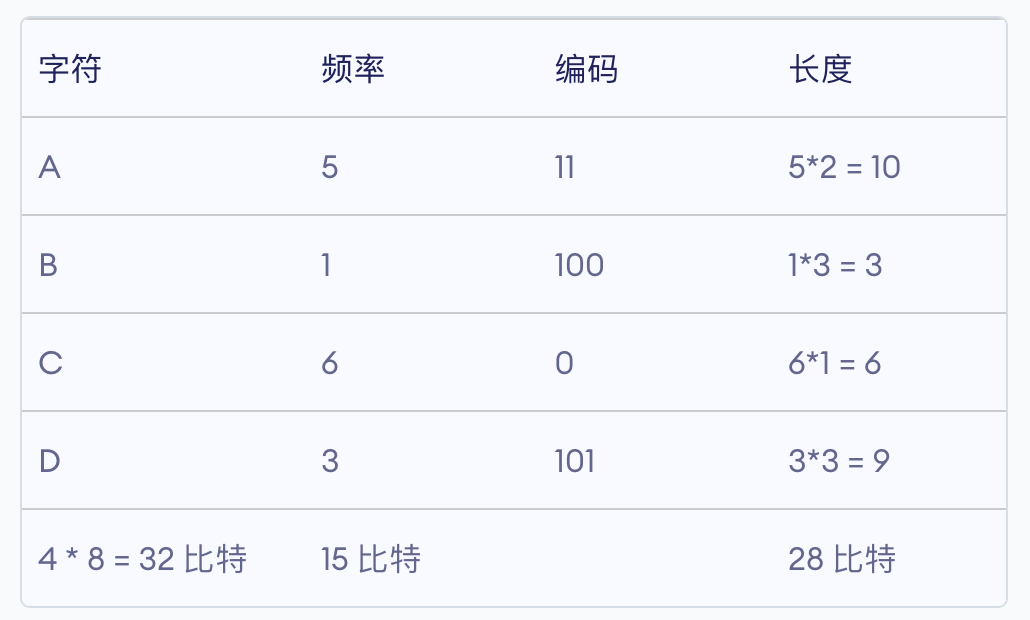
根据原文进行验证吧:
\[\large BCAADDDCCACACAC \]从本质上讲,哈夫曼编码是将最宝贵的资源(最短的编码)给出现概率最多的数据。
在上面的例子中,\(C\) 出现的频率最高,它的编码为 \(0\),就省下了不少空间。
三、特点
哈夫曼编码有三个特点:
- 带权路径长度\(WPL\)最短且唯一
- 编码互不为前缀(一个编码不是另一个编码的开头)
- 哈夫曼树和编码都不唯一
\(Q\):为什么通过哈夫曼编码后得到的二进制码不会有前缀的问题呢?
这是因为在哈夫曼树中,每个字母对应的节点都是叶子节点,而他们对应的二进制码是由根节点到各自节点的路径所决定的,正因为是叶子节点,每个节点的路径不可能和其他节点有前缀的关系。
\(Q2\):为什么通过哈夫曼编码获得的二进制码短呢?
因为哈夫曼树是带权路径长度最短的树,权值较大的节点离根节点较近。而带权路径长度是指:树中所有的叶子节点的权值乘上其到根节点的路径长度,这与最终的哈夫曼编码总长度成正比关系的。