前言
存疑点待补。有问题欢迎指出。想要题目部分源码请私信。
有笨蛋连续 \(2\) 年第一题都错。乐。考前看了一眼一考就忘。
如果不出意外的话,这是我最后一次更新初赛解析了。
老样子,代码题的代码待补。
选择题
1.在 Linux 系统终端中,用于切换工作目录的命令为( )。
A.
lsB.cdC.cpD.all
ls 命令用于显示指定工作目录下之内容(列出目前工作目录所含之文件及子目录)。
cd 命令用于切换当前工作目录。
cp 命令主要用于复制文件或目录。
all 我也不知道这干啥。
故选 B。
2.你同时用 time 命令和秒表为某个程序在单核 CPU 的运行计时。假如 time 命令的输出如下:
real 0m30.721s user 0m24.579s sys 0m6.123s以下最接近秒表计时的时长为( )。
A. 30s B. 24s C. 18s D. 6s
先解释一下 \(3\) 个时间,real 是程序的实际运行时间,sys 是内核态的时间,user 是用户态的时间。
而 real 用时包括 CPU 用时和所有延迟程序的执行的因素的和。CPU 用时被分为 sys 和 user 两块。
user 表示程序本身,以及它调用库中的子例程使用的时间;sys 是由程序直接或间接调用的系统调用的系统时间。
所以有 real = CPU 用时 + 其他因素的时间。CPU 用时 = user + sys。
于是有 real > user + sys。
故选 A。
3.若元素
a,b,c,d,e,f依次进栈,允许进栈、退栈操作交替进行,但不允许连续三次退栈操作,则不可能得到的出栈序列是( )。A.
dcebfaB.cbdaefC.bcaefdD.afedcb
又是原题拿来改改()。
A 是 进进进进退退进退退进退退。
B 是 进进进退退进退退进退进退。
C 是 进进退进退退进进退进退退。
D 是 进退进进进进进退退退退退。
退!退!退!
故选 D。
4.考虑对 \(n\) 个数进行排序,以下最坏时间复杂度低于 \(\mathcal{O}(n^2)\) 的排序方法是( )。
A. 插入排序 B. 冒泡排序 C. 归并排序 D. 快速排序
又要拿老图了。
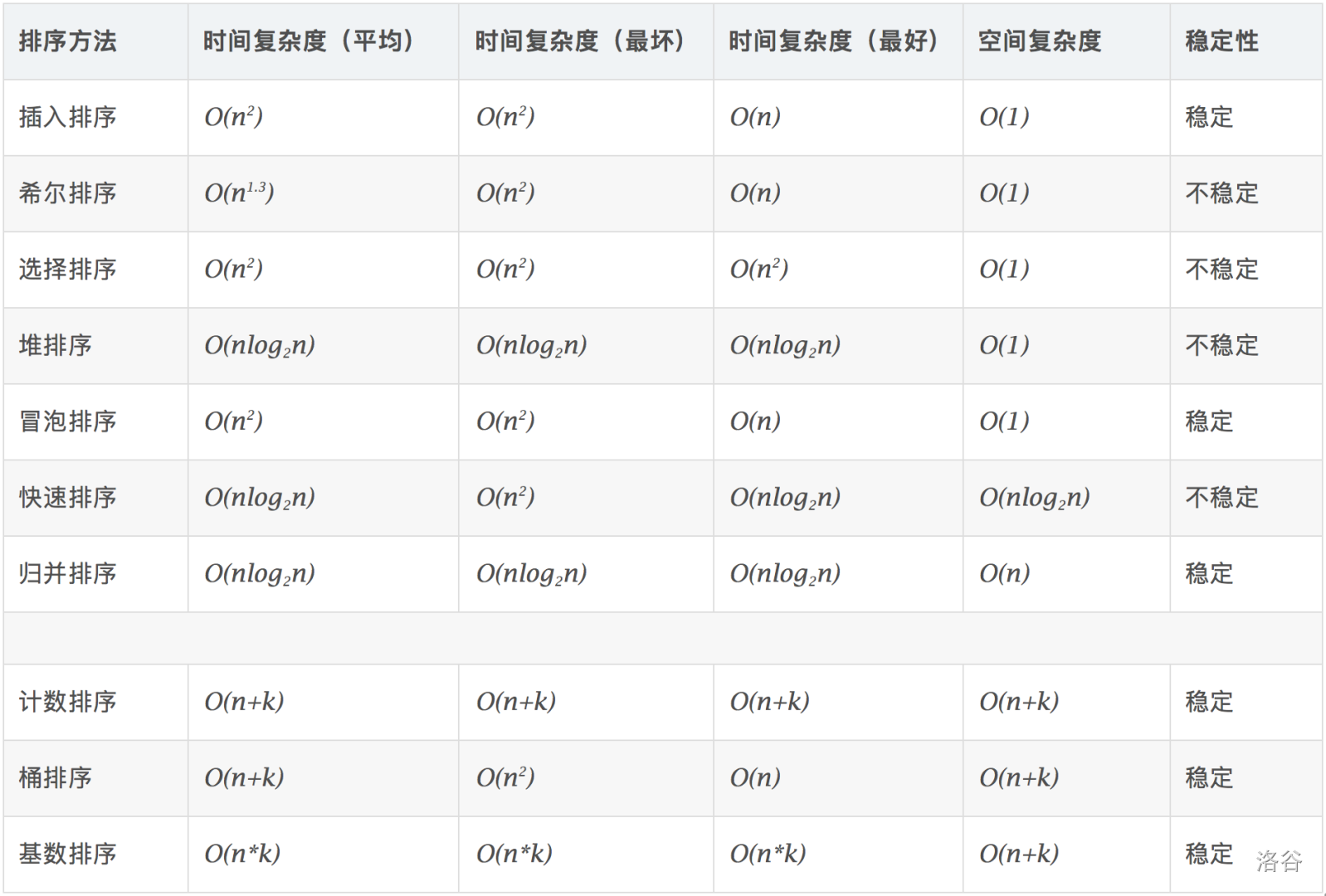
故选 C。
5.假设在基数排序过程中,受宇宙射线的影响,某项数据异变为一个完全不同的值。请问排序算法结束后,可能出现的最坏情况是( )。
A. 移除受影响的数据后,最终序列是有序序列。
B. 移除受影响的数据后,最终序列是前后两个有序的子序列。
C. 移除受影响的数据后,最终序列是一个有序的子序列和一个基本无序的子序列。
D. 移除受影响的数据后,最终序列基本无序。
?宇宙射线?
可以看看后面程序题,他甚至给了一个基排的框架()。
故选 A。
6.计算机系统用小端(Little Endian)和大端(Big Endian)来描述多字节数据的存储地址顺序模式,其中小端表示将低位字节数据存储在低地址的模式、大端表示将高位字节数据存储在低地址的模式。在小端模式的系统和大端模式的系统分别编译和运行以下 C++代码段表示的程序,将分别输出什么结果?( )
unsigned x = 0xDEADBEEF; unsigned char * p = (unsigned char * )&x; printf("%X", * p);A.
EF、EFB.EF、DEC.DE、EFD.DE、DE
根据题意,低位的就是选最低位的的 EF。高位的就是选择最高位的 DE。
故选 B。
7.一个深度为 \(5\)(根结点深度为 \(1\))的完全 \(3\) 叉树,按前序遍历的顺序给结点从 \(1\) 开始编号,则第 \(100\) 号结点的父结点是第( )号。
A. 95 B. 96 C. 97 D. 98
赛时的做法可能有点笨。
首先 \(5\) 层的完全树节点是 \(1+3+3^2+3^3+3^4 = 121\)。
所以根节点的每个儿子的子树大小是 \(40\)。
于是发现 \(100\) 号应该在第三个子树内,编号为 \(82 \sim 121\)。
同样的,一个层为 \(3\) 的满三叉树有节点 \(13\) 个,然后发现 \(100\) 号在当前第三个子树内。
然后数量级很小,手动画图一下就可以了。
故选 C。
8.强连通图的性质不包括( ):
A. 每个顶点的度数至少为 \(1\)。 B. 任意两个顶点之间都有边相连。
C. 任意两个顶点之间都有路径相连。 D. 每个顶点至少都连有一条边。
B 是完全图的定义。连通图不一定满足。
故选 B。
9.每个顶点度数均为 \(2\) 的无向图称为“\(2\) 正规图”。由编号为从 \(1\) 到 \(n\) 的顶点构成的所有 \(2\) 正规图,其中包含欧拉回路的不同 \(2\) 正规图的数量为( )。
A. \(n!\) B. \((n-1)!\) C. \(\dfrac{n!}{2}\) D. \(\dfrac{(n-1)!}{2}\)
当然你可以手算出 \(n=3\) 的情况然后带入选项。
注意到 \(n\) 个点最后一定会组成若干个环。但是如果要存在欧拉回路就一定要联通,意味着最后是一个大环。
圆排列,为 \((n-1)!\),但因为边是无向的所以还可以镜面反转,所以最后答案为 \(\dfrac{(n-1)!}{2}\) 。
故选 D。
10.共有 \(8\) 人选修了程序设计课程,期末大作业要求由 \(2\) 人组成的团队完成。假设不区分每个团队内 \(2\) 人的角色和作用,请问共有多少种可能的组队方案。( )
A. 28 B. 32 C. 56 D. 64
你这题目怎么还有歧义啊?
根据题意相当于 \(\dbinom{8}{2} = 28\)。
故选 A。
11.小明希望选到形如“省 \(\texttt{A} \cdot \mathcal{LLDDD}\)”的车牌号。车牌号在“·”之前的内容固定不变;后面的 5 位号码中,前 \(2\) 位必须是大写英文字母,后 \(3\) 位必须是阿拉伯数字(\(\mathcal{L}\) 代表 \(\texttt{A}\) 至 \(\texttt{Z}\), \(\mathcal{D}\) 表示 \(\texttt{0}\) 至 \(\texttt{9}\),两个 \(\mathcal{L}\) 和三个 \(\mathcal{D}\) 之间可能相同也可能不同)。请问总共有多少个可供选择的车牌号。( )
A. 20280 B. 52000 C. 676000 D. 1757600
\(10^3 \times 26^2 = 676000\)。
故选 C。
12.给定地址区间为 \(0 \sim 9\) 的哈希表,哈希函数为 \(h(x) = x \bmod 10\),采用线性探查的冲突解决策略(对于出现冲突情况,会往后探查第一个空的地址存储;若地址 \(9\) 冲突了则从地址 \(0\) 重新开始探查)。哈希表初始为空表,依次存储 \((71, 23, 73, 99, 44, 79, 89)\) 后,请问 \(89\) 存储在哈希表哪个地址中。( )
A. 9 B. 0 C. 1 D. 2
浅浅模拟一下。
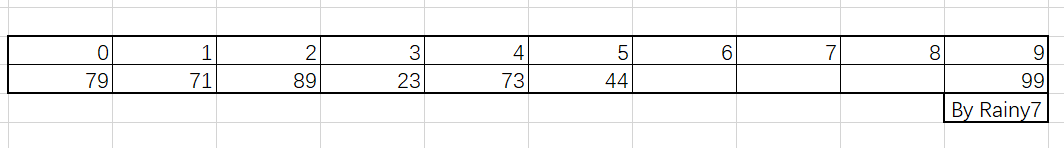
故选 D。
13.对于给定的 n,分析以下代码段对应的时间复杂度,其中最为准确的时间复杂度为( )。
int i, j, k = 1; for (i = 0; i < n; i++) { for (j = 0; j < n; j*=2) { k = k + n / 2; } }A. \(\mathcal{O}(n)\) B. \(\mathcal{O}(n \log n)\) C. \(\mathcal{O}(n\sqrt{n})\) D. \(\mathcal{O}(n^2)\)
第一层为 \(n\) ,第二层为 \(\log n\)。
故选 B。
14.以比较为基本运算,在 \(n\) 个数的数组中找最大的数,在最坏情况下至少要做( )次运算。
A. \(\dfrac{n}{2}\)
B. \(n-1\)
C. \(n\)
D. \(n+1\)
最坏情况下,每个数都会被比较一次。但注意第一次不需要比较。
故选 B。
15.
ack函数在输入参数(2,2)时的返回值为( )。unsigned ack(unsigned m, unsigned n) { if (m == 0) return n + 1; if (n == 0) return ack(m - 1, 1); return ack(m - 1, ack(m, n - 1)); }A. 5 B. 7 C. 9 D. 13
赛时并没有发现他有什么意义。是手模的。
偷个懒,这里不放模拟过程了。
故选 B。
阅读程序
(1)
先简单看一下程序,后半部分看上去就很 KMP。但前面求的并不是失配数组。
他存下了每个字符的最短后缀。然后有一个类似失配的跳跃过程。
16.当输入为 \(\texttt{abcde fg}\) 时,输出为 \(-1\)。( )
因为程序是在匹配,所以显然这个没有匹配结果。
故判对。
17.当输入为 \(\texttt{abbababbbab abab}\) 时,输出为 \(4\)。 ()
眼睛看一下发现第一次匹配成功确实是在第 \(4\) 个位置。
但是这题是从 \(0\) 开始存储的,实际输出应该为 \(3\)。
故判错。
18.当输入为 \(\texttt{GoodLuckCsp2022 22}\) 时,第 \(20\) 行的
j++语句执行次数为 \(2\)。( )
看上去匹配次数为 \(3\),但是到 \(p\) 的时候会直接跳到后 \(3\) 个位置,所以实际上只会执行 \(2\) 次。
故判对。
19.该算法最坏情况下的时间复杂度为( )。
A. \(\mathcal{O}(n+m)\) B. \(\mathcal{O}(n \log m)\) C. \(\mathcal{O}(m \log n)\) D. \(\mathcal{O}(nm)\)
前面已经说过,他只存储了每个字符的跳跃的最小值。
考虑怎么卡满。
构造 \(s= \texttt{aaaaaaaaaaa} , t= \texttt{aaaab}\)。
此时因为 \(a\) 跳跃只有 \(2\),所以复杂度为 \(\mathcal{O}(nm)\)。
故选 D。
20.
f(a, b)与下列( )语句的功能最类似。A.
a.find(b)B.a.rfind(b)C.
a.substr(b)D.a.compare(b)
前面说过了是匹配过程。
故选 A。
21.当输入为 \(\texttt{baaabaaabaaabaaaa aaaa}\),第 \(20\) 行的
j++语句执行次数为( )。A. 9 B. 10 C. 11 D. 12
模拟一下就可以了。注意跳跃会跳过一些 \(\texttt{a}\)。
故选 B。
(2)
哇。是基排!但是每一位排序完都覆盖掉上一位排序了(?)。
简单来说,就是基于 \(k\) 进制下,对于每一位的排序。
22.这是一个不稳定的排序算法。( )
for (int j = n - 1; j >= 0; j--)
与
cnt[val[j] / base % k]--;
意味着相同的数都是从前往后放。
换言之,排序的过程中,如果两个相等的值,设编号 \(i<j\),不可能出现排完序后变成 \(i>j\) 的情况。
所以他是稳定的。
故判错。
23.该算法的空间复杂度仅与 \(n\) 有关。( )
可以发现 cnt[] 是和 \(k\) 的大小有关的。
故判错。
24.该算法的时间复杂度为 \(\mathcal{O}(m(n+k))\)。( )
第一层是 \(m\) 的,第二层是 \((n+k)\) 的。
故判对。
25.当输入为
5 3 98 26 91 37 46时,程序第一次执行到第 \(36\) 行,val[]数组的内容依次为( )。A.
91 26 46 37 98B.91 46 37 26 98C.
98 26 46 91 37D.91 37 46 98 26
第一次意味着就是 \(3\) 进制下的第一位的比较。
也就是比较 \(2,2,1,1,1\)。另外他是稳定的。
故选 D。
26.若
val[i]的最大值为 \(100\),\(k\) 取( )时算法运算次数最少。A. 2 B. 3 C. 10 D. 不确定
虽然 \(m = \log_k(n)\) 的,但是复杂度还和 \(n\) 的大小有关。
注意到 \(n\) 不同时,选的 \(k\) 也不同。
故选 D。
27.当输入的 \(k\) 比
val[i]的最大值还大时,该算法退化为( )算法。A. 选择排序 B. 冒泡排序 C. 计数排序 D. 桶排序
这意味着数只有一位。其实我觉得他像桶排。
故选 C。
(3)
此题存疑。你先别急。
看到输出部分应该是一个类似进制转换的东西。
但是前面那一块写的非常迷惑,虽然取膜负数但注意其实本质还是,取膜一个正数。因为他有写一个取整,所以余数一定是正数。
然后接下来就是模拟了。
28.该算法的时间复杂度为 \(\mathcal{O}(\log_k n)\)。( )
说实话我不知道为什么他是错的。待补。
故判错。
29.删除第 \(23\) 行的强制类型转换,程序的行为不变。( )
如果没有强制类型转换,那么会输出一个 int 的整数。
故判错。
30.除非输入的 \(n\) 为 \(0\),否则程序输出的字符数为 \(\mathcal{O}(\left\lfloor \log_k|n| \right\rfloor +1)\)。( )
注意到 \(m\) 是这个级别的。如果最后有余数会 \(+1\)。
故判对。
31.当输入为
100 7时,输出为( )。A. 202 B. 1515 C. 244 D. 1754
下面这几题建议直接进制转换或者模拟解决问题。
故选 A。
32.当输入为
-255 8时,输出为“( )”。A. 1400 B. 1401 C. 417 D. 400
故选 B。
33.当输入为
1000000 19时,输出为“( )”。A. BG939 B. 87GIB C. 1CD428 D. 7CF1B
故选 B。
完善程序
(1)
(归并第 \(k\) 小) 已知两个长度均为 \(n\) 的有序数组 \(a1\) 和 \(a2\)(均为递增序,但不保证严格单调递增),并且给定正整数 \(k(1 \le k \le 2n)\),求数组 \(a1\) 和 \(a2\) 归并排序后的数组里第 \(k\) 小的数值。
试补全程序。
看题目更直接吧。
- ①处应填( )
A.
(m1 + m2) * 2B.(m1 - 1) + (m2 - 1)C.
m1 + m2D.(m1 + 1) + (m2 + 1)
可以由后面推断出这里是要求出,当前二分出两个序列的长度和。
注意一下存储是从 \(0\) 开始的。
(目前存疑)所以为什么选 C 啊。我觉得应该选 D?
- ②处应填( )
A.
a1[m1] == a2[m2]B.a1[m1] <= a2[m2]C.
a1[m1] >= a2[m2]D.a1[m1] != a2[m2]
注意到,两者较大的会放在合并序列的最后。
假设 \(a2\) 是合并序列的最后一个,那么意味着如果 \(m2\) 后移动,后面的所有数字都是 \(a2\)。
分析到这里差不多了,注意到他是 cnt<k 的时候把 \(m1\) 往右移。
故选 B。
- ③处应填( )
A.
left1 == right1B.left1 < right1C.
left1 > right1D.left1 != right1
注意到二分结束条件是 \(l_1 > r_1\) 或者 \(l_2>r_2\)。
所以一定是这两种情况分类。且一定是不满足的这对,的数量一定满足是前 \(k\) 大的。且他的恭喜为 \(a_{0} \dots a_{l-1}\)。
到这里很清晰了。
故选 C。
- ④处应填( )
A.
y = a1[k - left2 - 1]B.y = a1[k - left2]C.
y = a2[k - left1 - 1]D.y = a2[k - left1]
- ⑤处应填( )
A.
y = a1[k - left2 - 1]B.y = a1[k - left2]C.
y = a2[k - left1 - 1]D.y = a2[k - left1]
这两题一样的。
根据上面的分析,是已知一个 \(a_{0} \dots a_{l-1}\) 的贡献下,求另一个 \(a\) 的贡献。
因为总数是 \(k\),所以可以很直接得到另一个 \(a\) 的长度。
注意一下下标从 \(0\) 开始。
故 37 选 C。38 选 A。
(2)
(容器分水) 有两个容器,容器 \(1\) 的容量为为 \(a\) 升,容器 \(2\) 的容量为 \(b\) 升;同时允许下列的三种操作,分别为:
FILL(i):用水龙头将容器 \(i(i \in \{ 1,2 \})\) 灌满水;DROP(i):将容器 \(i\) 的水倒进下水道;POUR(i,j):将容器 \(i\) 的水倒进容器 \(j\)(完成此操作后,要么容器 \(j\) 被灌满,要么容器 \(i\) 被清空)。求只使用上述的两个容器和三种操作,获得恰好 \(c\) 升水的最少操作数和操作序列。上述 \(a,b,c\) 均为不超过 \(100\) 的正整数,且 \(c \le \max \{a,b \}\)。
试补全程序。
?我祖传的状压题呢?
这题还没上一题难吧()。
39.①处应填( )
A.
dfs(x + t, y - t) + 1B.dfs(x + t, y - t) - 1C.
dfs(x - t, y + t) + 1D.dfs(x - t, y + t) - 1
40.②处应填( )
A.
dfs(x + t, y - t) + 1B.dfs(x + t, y - t) - 1C.
dfs(x - t, y + t) + 1D.dfs(x - t, y + t) - 1
就是两个容器互倒。
故 39 选 A,40 选 C。
41.③处应填( )
A.
x == c || y == cB.x == c && y == cC.
x >= c || y >= cD.x >= c && y >= c
判断结束条件,有一个是 \(c\) 即可。
故选 A。
42.④处应填( )
A.
dfs(x + t, y - t) + 1B.dfs(x + t, y - t) - 1C.
dfs(x - t, y + t) + 1D.dfs(x - t, y + t) - 1
43.⑤处应填( )
A.
dfs(x + t, y - t) + 1B.dfs(x + t, y - t) - 1C.
dfs(x - t, y + t) + 1D.dfs(x - t, y + t) - 1
和前面 \(2\) 题本质一样的。
故 42 选 A。43 选 C。
\[\text{by Rainy7} \] 标签:故选,texttt,dfs,a2,初赛,2022,mathcal,排序,CSP From: https://www.cnblogs.com/Rainy7/p/csp-s-2022-first.html