线段树
基本思想
将 [1,n] 分解成若干特定的子区间(数量不超过 4×n),然后,将每个区间 [l,r] 都分解为
少量特定的子区间,通过对这些少量子区间的修改或者统计,来实现快速对 [l,r] 的修改或者统计。
可以解决的问题
满足加法性质的运算的区间问题,如区间和,区间异或,区间 $\gcd$ 等。
不能解决的问题
区间众数等不符合区间加法性质的问题。
原理与实现
线段树通过递归将 $[l,r]$ 的一个区间分为 $[l,mid],[mid+1,r]$,直到 $l=r$。
如果根的高度为 $1$,那么对于区间 $[1,n]$ 建立这棵线段树的高度最高为 $\lfloor{\log (n-1)}\rfloor+2$。
通过一张图来解释线段树对于 $[1,9]$ 的建树过程。
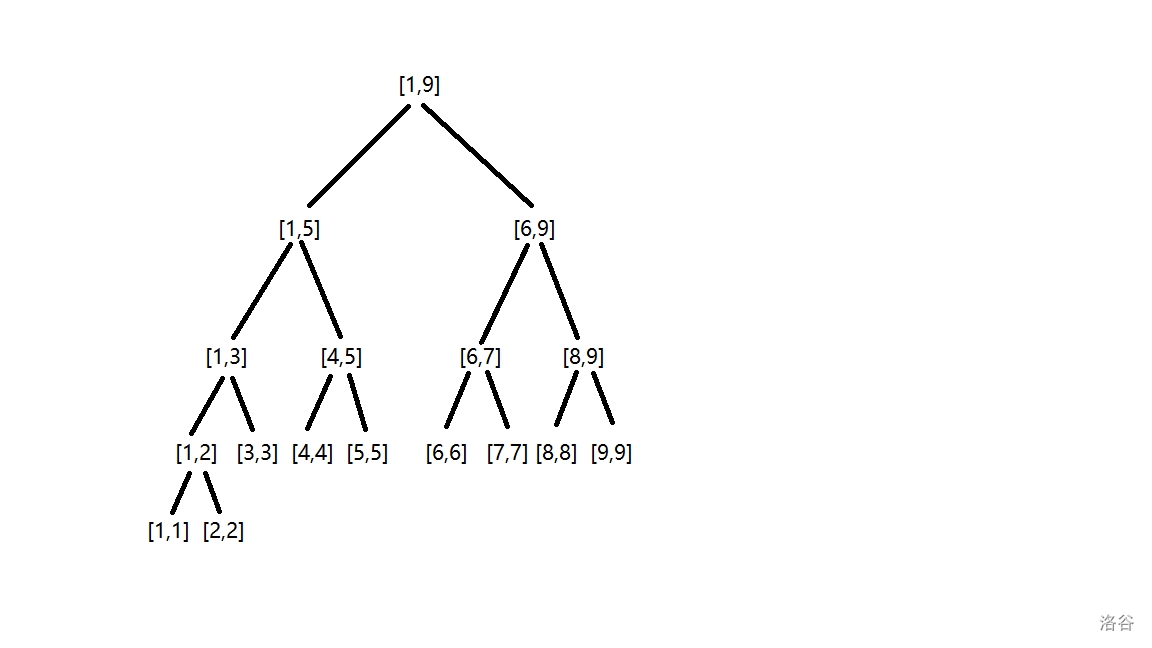
单点查询
单点查询实际上就是定位到线段树的叶子结点。
我们现在假设我们需要定位到 $x$,那么我们就是去找 $[x,x]$ 这个区间。考虑递归,如果 $x \le mid$,显然 $[x,x]$ 在右子树中,反之则在左子树中。
单点修改
进行单点修改,首先也需要定位到这个结点(同单点查询)。然后修改完成后,我们需要一路往上更新,这样才能保证线段树的正确性。
区间查询
假设查询区间为 $[l,r]$,我们从 $[1,n]$ 开始递归查询 $[L,mid]$ 与 $[mid+1,R]$。此时对递归区间进行分类讨论:
-
当前区间被目标区间完全包含。此时直接返回当前区间的值即可。
-
当前区间与目标区间无交集。此时返回 $0$。
-
当前区间没有被目标区间包含且有交。此时递归处理左子树与右子树。
区间修改
需要进行区间修改的时候,我们需要引入一个新东西:懒标记。
对于一个区间 $[l,r]$来说,我们如果每次都更新区间中的每一个值,那样的话更新的复杂度将会是 $O(n \log n)$。
这个复杂度甚至比暴力还高。所以我们引入了懒标记。
懒标记的主要原理是区间修改操作时先对这个区间打上标记,暂时不进行更新,若之后需要用到该节点的信息时再进行更新。
单打标记的复杂度为一个常数。
时空复杂度
单次操作时间复杂度为 $O(\log n)$。
空间复杂度为 $O(4n)$。
模板
这里以区间加法为例。
struct node{
int l,r;
ll v,tag;
}a[400001];
int n,m;
ll t[100001],sum[100001];
int ls(int u){
return u<<1;
}
int rs(int u){
return (u<<1)|1;
}
bool inrange(int L,int R,int l,int r){
return (L<=l)&&(r<=R);
}
bool outofrange(int L,int R,int l,int r){
return (R<l)||(r<L);
}
void build(int u,int L,int R){
a[u]=(node){L,R,sum[R]-sum[L-1],0};
if(L!=R){
int M=L+R>>1;
build(ls(u),L,M);
build(rs(u),M+1,R);
}
}
void pushup(int u){
a[u].v=a[ls(u)].v+a[rs(u)].v;
}
void pushdown(int u){
int L=a[u].l,R=a[u].r,M=L+R>>1,K=a[u].tag;
if(L==R) return ;
a[u].tag=0;
a[ls(u)].tag+=K;
a[rs(u)].tag+=K;
a[ls(u)].v+=K*(M-L+1);
a[rs(u)].v+=K*(R-M);
}
void update(int u,int L,int R,ll k){
if(a[u].tag) pushdown(u);
if(inrange(L,R,a[u].l,a[u].r)){
a[u].tag+=k;
a[u].v+=k*(a[u].r-a[u].l+1);
pushdown(u);
}
else if(!outofrange(L,R,a[u].l,a[u].r)){
update(ls(u),L,R,k);
update(rs(u),L,R,k);
pushup(u);
}
}
ll search(int u,int L,int R){
if(a[u].tag) pushdown(u);
if(inrange(L,R,a[u].l,a[u].r)){
return a[u].v;
}
else if(!outofrange(L,R,a[u].l,a[u].r)){
return search(ls(u),L,R)+search(rs(u),L,R);
}
else return 0ll;
}
题目
P3372、P3373、P1253、P4145、P1198、P1531、P1471、P1972、P1438
树状数组
基本思想
树状数组的核心思想是将一个需要操作的区间分解成若干小区间,在维护的时候,直接对这些小区间进行处理,在查询的时候再将这些区间组装成我们想要的区间。
可以解决的问题
满足减法性质的运算的区间问题,如区间和,区间异或等。
不能解决的问题
区间众数,区间 $\gcd$ 等不符合区间加法性质的问题。
原理与实现
这个玩意大概长成这个样子:
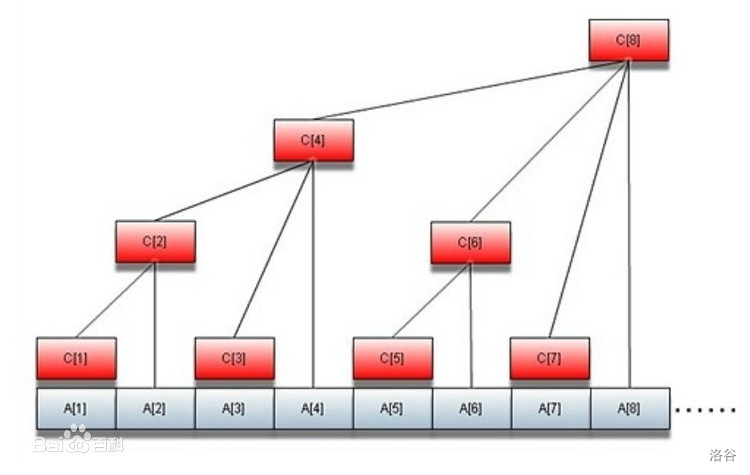
(这里用了百度的图片)
它就是一个特殊的前缀和数组。
仔细观察红色框内与灰色框的关系:
$c_1=a_1$
$c_2=a_1+a_2$
$c_3=a_3$
$c_4=a_1+a_2+a_3+a_4$
$c_5=a_5$
$c_6=a_5+a_6$
$c_7=a_7$
$c_8=a_5+a_6+a_7+a_8$
于是可以发现以下规律:
$c_i=a_{i-2k+1}+a_{i-2k+2}+\dots+a_i$
那么找出 $i$ 的二进制下最低位的 $1$ ,然后一步步往上更新便可实现 $O(\log n)$ 单点修改。
那么问题来了,怎么获取最低位的 $1$?
这时候就要引入 $lowbit$ 函数了。原理如下:
先假设该数最低位的 $1$ 在第 $k$ 位上,则按位取反的二进制的第 $k$ 位为 $0$,$0$ 到 $k-1$ 位全部为1。由于进位,$0$ 到 $k-1$ 位全部为 $0$,第 $k$ 位为 $1$,剩下的数位仍然和原来相反。那么 x&(-x) 自然就只剩下最低位的 $1$ 以及它后面的 $0$ 构成的数值了。
知道了以上知识以后,便可以写出修改函数:
void add(int x,ll y){//在位置x的数加上y
for(int i=x;i<=n;i+=lowbit(i)){
c[i]+=y;
}
}
那么上面那个公式可以这么写:
$c_i=\sum^i_{j=i-lowbit(i)+1} a_i$
那么在跑代码的过程中,数据结构内部发生了啥?这里用 $add(5,1)$ 来举例:
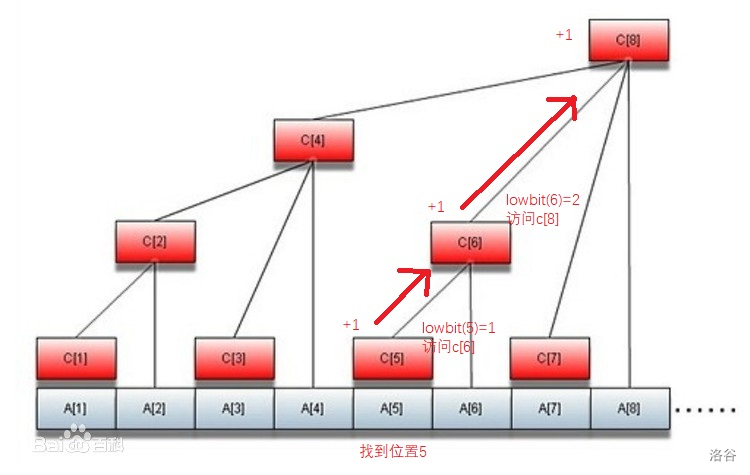
可以看到,我们要想单点修改 $a[5]$,则需修改所有包含 $a[5]$ 的区间值,在本例中即为 $c[5],c[6],c[8]$。
区间查询
利用前缀和思想,我们可以知道求 $a_x$ 到 $a_y$ 的和就是求 $a_1$ 到 $a_y$ 的和减去 $a_1$ 到 $a_{x-1}$ 的和。
那么把问题拆开来看,如何求 $a_1$ 到 $a_x$ 的和?
我们可以先将 $c_i$ 加入答案,此时我们的问题变成了求 $a_1$ 到 $a_i-lowbit(i)$ 的和。
那么我们接下来可以将 $c_{i-lowbit(i)}$ 加入答案。
不断重复以上操作,直到 $i$ 变为 $0$。那么此时我们已经得到答案。
代码如下:
ll search(int x,int y){//查询x到y的和
int sum1=0,sum2=0;
for(int i=x-1;i;i-=lowbit(i)){
sum1+=c[i];
}
for(int i=y;i;i-=lowbit(i)){
sum2+=c[i];
}
return sum2-sum1;
}
我们还是来看看树状数组内部发生的事情,这里拿查询区间 $[4,6]$ 举例。
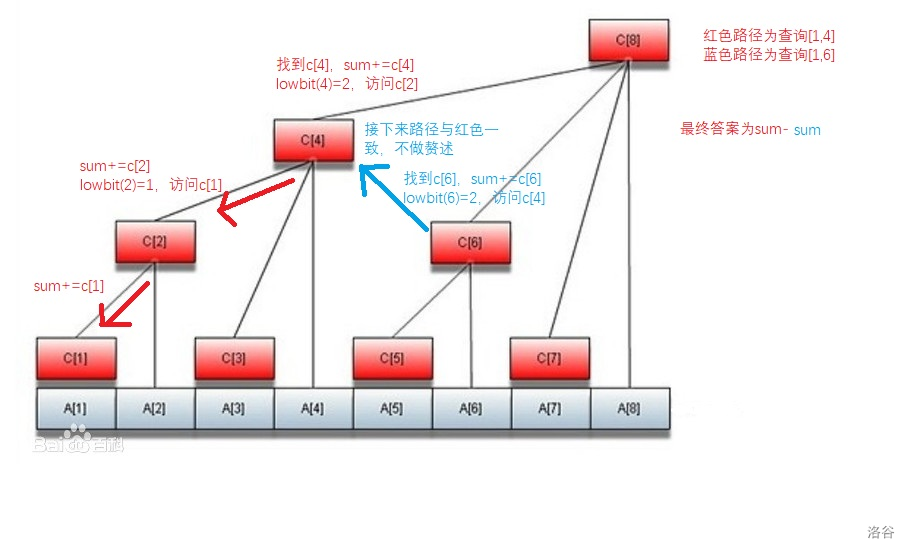
可以看到每一步中,都把 $x$ 变成了 $lowbit(x)$,结合 $lowbit$ 函数的概念,相当于不断去掉 $x$ 二进制中最低位的那个 $1$。由于 $i$ 的二进制表示位数不超过 $\log i$,所以单点查询复杂度为 $O(\log n)$。
模板
#include <bits/stdc++.h>
#define ll long long
#define lowbit(x) ((x)&(-x))
using namespace std;
int n,m;
ll a[500001],c[500001];
void add(int x,ll k){
for(int i=x;i<=n;i+=lowbit(i)){
c[i]+=k;
}
}
ll search(int x,int y){
int sum1=0,sum2=0;
for(int i=x-1;i;i-=lowbit(i)){
sum1+=c[i];
}
for(int i=y;i;i-=lowbit(i)){
sum2+=c[i];
}
return sum2-sum1;
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
scanf("%lld",&a[i]);
add(i,a[i]);
}
for(int i=1;i<=m;i++){
int op;
scanf("%d",&op);
if(op==1){
int x;
ll k;
scanf("%d%lld",&x,&k);
add(x,k);
}
else{
int x,y;
scanf("%d%d",&x,&y);
printf("%lld\n",search(x,y));
}
}
return 0;
}
题目
P3374、P3368、P3372、P4939、P5057、CF652D、CF61E、SP3267、P3531
ST表
基本思想
预处理+倍增。
可以解决的问题
满足不重复贡献的问题,如 RMQ 问题与区间 $\gcd$。
不能解决的问题
不满足不重复贡献性质,如区间和。
因为 ST 表需要预处理,所以也不能处理动态区间问题。
动态RMQ还是写带修莫队罢
原理与实现
预处理
使用一个二维数组存储一定范围信息,例如 $f_{i,j}$ 表示区间 $[i, i+2^j)$的信息。预处理的主要思想为倍增。一个区间的最值来自在左半部分与右半部分的最值。
for(int i=1;(1<<i)<=n;i++){
for(int j=1;j<=n;j++){
if(j+(1<<i)-1<=n){
st[j][i]=max(st[j][i-1],st[j+(1<<(i-1))][i-1]);
}
}
}
查询
对于区间 $[l,r]$,我们令 $k=\log(r−l+1)$,那么 $[l+2k,r−2k+1]$ 必然会覆盖原来的区间,尽管可能会有重叠部分,但因为满足不重复贡献性质,所以并不影响结果。
for(int i=1;i<=m;i++){
int l,r,k;
scanf("%d%d",&l,&r);
k=log2(r-l+1);
printf("%d\n",max(st[l][k],st[r-(1<<k)+1][k]));
}
模板
#include<bits/stdc++.h>
using namespace std;
int n,m,a[100001],st[100001][31];
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
st[i][0]=a[i];
}
for(int i=1;(1<<i)<=n;i++){
for(int j=1;j<=n;j++){
if(j+(1<<i)-1<=n){
st[j][i]=max(st[j][i-1],st[j+(1<<(i-1))][i-1]);
}
}
}
for(int i=1;i<=m;i++){
int l,r,k;
scanf("%d%d",&l,&r);
k=log2(r-l+1);
printf("%d\n",max(st[l][k],st[r-(1<<k)+1][k]));
}
return 0;
}
题目
并查集
基本思想
通过合并操作来快速查询一个元素是否在一个集合中。
可以解决的问题
-
某些集合问题。如[ABC293D][def]。
-
图的联通性问题。如P1197。
-
最小生成树。
原理与实现
初始化
我们设 $f_i$ 为 $i$ 的父亲节点。
一开始显然每个节点都只会有这一个元素,所以每个节点的父节点初始化为自己。
for(int i=1;i<=n;i++){
f[i]=i;
}
合并
如果要合并 $x$ 和 $y$ 所在的集合,很容易想到直接把 $f_x$ 设为 $y$ 就可以了。
查询
查询 $x$ 与 $y$ 是否在同一个集合,只要我们在并查集上爬树,如果他们有公共祖先则在一个集合。
路径压缩
为什么要路径压缩?
考虑并查集的这种情况:

这样的话,每次查询操作的时间复杂度就会退化为线性。
那么怎么进行路径压缩?
我们每次查询的时候直接把查询一路上的所有点的 $f$ 值直接设为最终查询的结果即可。
我们对上图进行路径压缩:
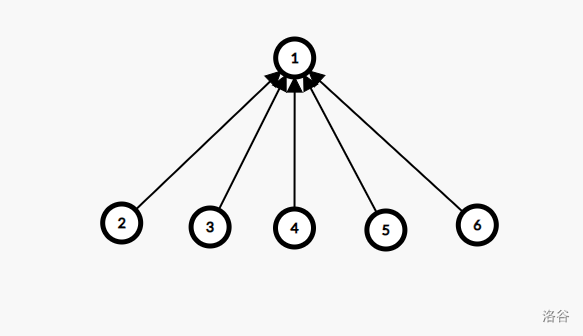
这样我们每次查询的时间复杂度就会变为 $O(1)$,大大优化了查询的效率。
模板
int find(int x){
if(f[x]!=x){
f[x]=find(f[x]);
}//路径压缩
return f[x];
}
void uunion(int x,int y){
f[find(x)]=find(y);
}
void init(){
for(int i=1;i<=n;i++){
f[i]=i;
}
}
题目
P1111、P1197、P1455、P1536、ABC293D、P1892、P2078、P2256、P2294、P2814
标签:大乱,int,lowbit,复杂度,查询,区间,数据结构,ll From: https://www.cnblogs.com/luqyou/p/17229809.html