数位DP
题目描述:计算从[l,r]中windy数的个数
windy数:不含前导零且任意相邻两位数字之差至少为2
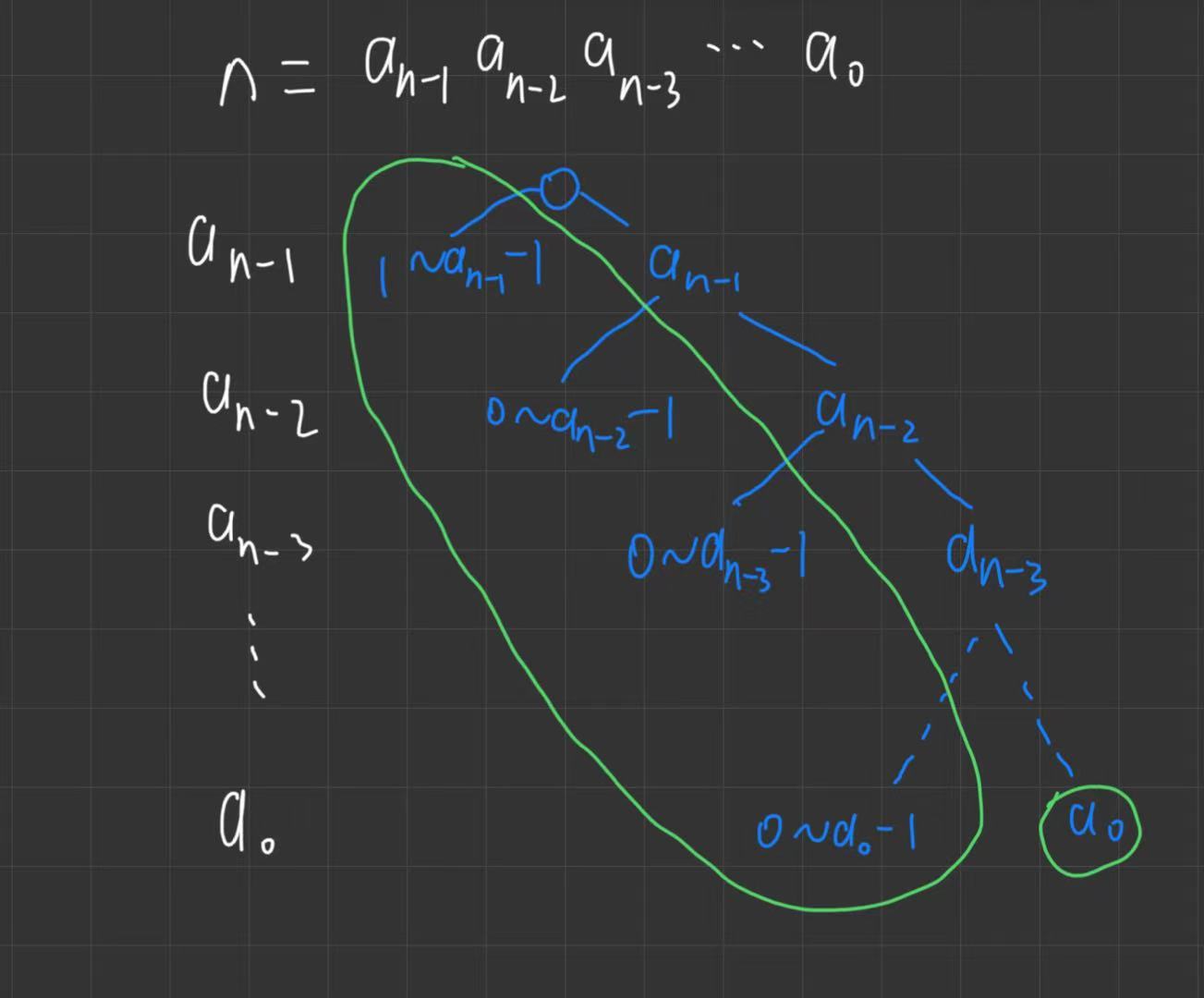
由于不含前导零,所以最高位不能从0开始,只能从1~x-1
考虑状态表示:
f[i][j]表示共有i位,且最高位为j的windy数的个数
状态转移:
f[i][j] += f[i - 1][k],其中abs(j-k)>=2
#include <iostream>
#include <cstring>
#include <vector>
const int N = 15;
// f[i][j]表示共有i位,最高位为j的windy数的个数
// 这里状态是包含前导零的
int f[N][10];
void init() {
for (int i = 0; i <= 9; i ++ ) f[1][i] = 1;
for (int i = 2; i < N; i ++ )
for (int j = 0; j <= 9; j ++ )
for (int k = 0; k <= 9; k ++ )
if (abs(j - k) >= 2)
f[i][j] += f[i - 1][k];
}
int cal(int n) {
if (!n) return 0;
std::vector<int> nums;
while (n) nums.push_back(n % 10), n /= 10;
// 由于第一位可以随便放,所以保证对任意x∈ (0,9),abs(pre,x)都成立即可
int res = 0, pre = -2;
for (int i = nums.size() - 1; i >= 0; i -- ) {
int x = nums[i];
// 最高位不能从0开始枚举
for (int j = i == nums.size() - 1; j < x; j ++ )
if (abs(j - pre) >= 2) res += f[i + 1][j];
if (abs(x - pre) < 2) break;
pre = x;
if (!i) res ++ ;
}
// 处理前导零的情况,也就是位数小于nums.size()的情况
// 例如14本来是windy数,由于前导零的存在,014中01是不满足条件的
// 所以f[3][0]会被筛掉,就会导致答案漏掉;
// 存在前导零则至少有一位,且最高位不是0
// 所以i从1开始,j也从1开始
for (int i = 1; i < nums.size(); i ++ )
for (int j = 1; j <= 9; j ++ )
res += f[i][j];
return res;
}
int main() {
init();
int l, r;
std::cin >> l >> r;
std::cout << cal(r) - cal(l - 1) << '\n';
return 0;
}