标签:int ed 合并 st 离散 second alls 区间
离散化
-
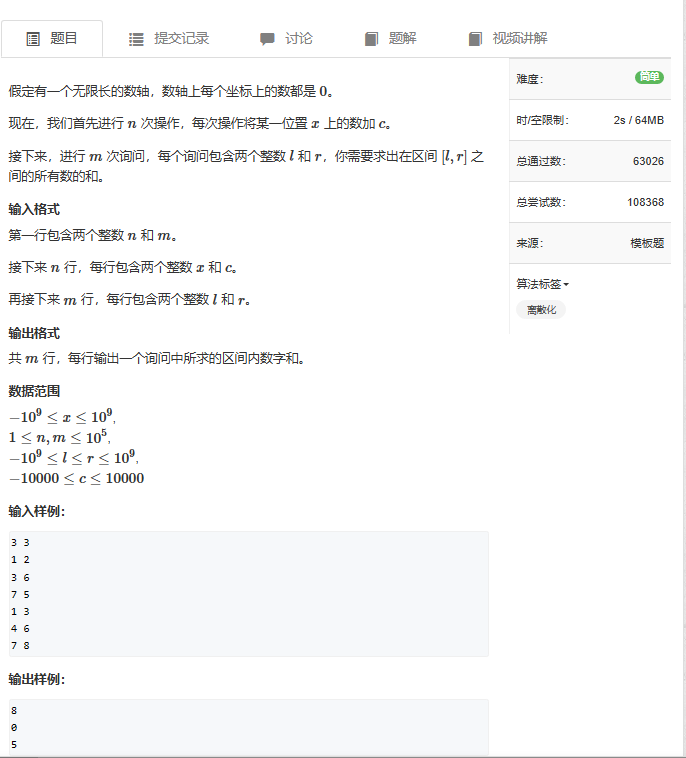
一个序列长度非常大(>10^5 一般10^9左右),但是有值的元素却十分稀疏
-
这里使用离散化映射+前缀和处理
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
const int N = 3e5+10;
int n,m;
//a[i] 存储的是插入下标位i的值
//s[i] 为a的前缀和
int a[N],s[N];
//存储所有需要离散化元素的下标(想一下包括题目中插入的下标x和询问的下标l和r)
vector<int>alls;
//存储插入和询问操作数据
vector<pair<int,int>> add,query;
//法一 二分查找的写法,哪里错了呢
// int find(int x){
// int l=0,r=alls.size()-1;
// while(l<=r){
// int mid=(l+r)>>1;
// if(x<a[mid]) r=mid-1;
// else if(x>a[mid]) l=mid+1;
// else{
// //映射为 1,2....n
// return mid+1;
// }
// }
// return -1;
// }
//法二 二分写法(二分要强于二分查找,二分查找仅适用于元素个数为1的时候)
int find(int x){
int l=0,r=alls.size()-1;
while(l<r){
int mid=l+r>>1;
if(alls[mid]>=x) r=mid;
else l=mid+1;
}
return r+1;
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++){
int x,c;
cin>>x>>c;
add.push_back({x,c});
alls.push_back(x);
}
for(int i=1;i<=m;i++){
int l,r;
cin>>l>>r;
query.push_back({l,r});
alls.push_back(l);
alls.push_back(r);
}
// alls 排序+去重
sort(alls.begin(),alls.end());
alls.erase(unique(alls.begin(),alls.end()),alls.end());
//初始化a[x]中有被插入的部分
for(auto item :add){
//通过假想的下标找到在a数组中对应的下标
int x=find(item.first);
a[x]+=item.second;
}
//前缀和
for(int i=1;i<=alls.size();i++){
s[i]=s[i-1]+a[i];
}
for(auto item:query){
int l=find(item.first);
int r=find(item.second);
cout<<s[r]-s[l-1]<<endl;
}
return 0;
}
-
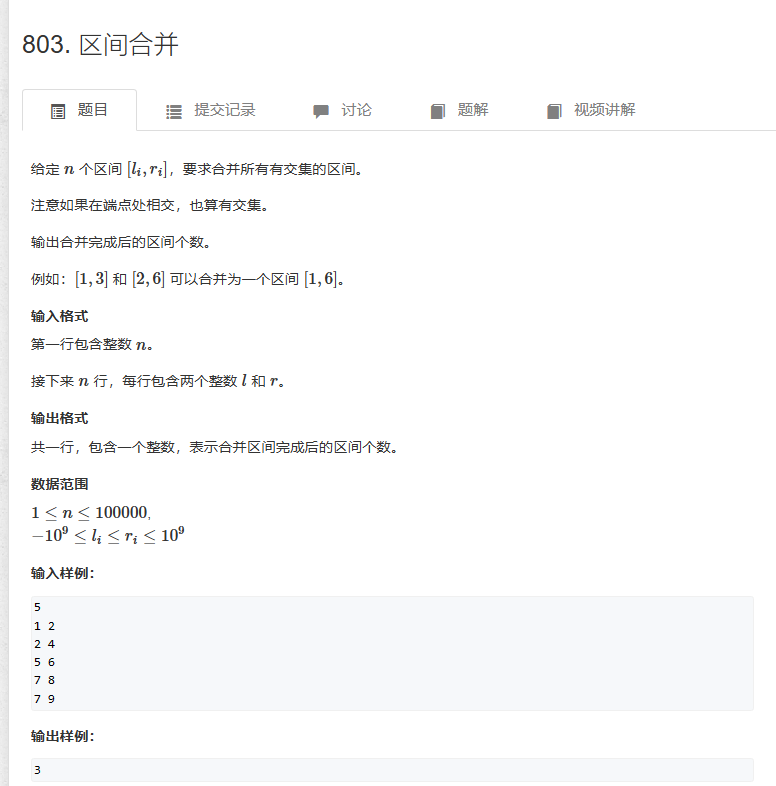
区间合并
-
区间合并,一般是对所有区间按照左(右)端点排序,然后维护一个中间变量区间(一般用第一个区间初试)[st,ed],然后后边的每一个区间和这个区间比较如果后面的这个区间的左端点<=变量区间的ed,那么说明他们有交集,那么变量区间的ed=max(ed,后一个区间.右端点),否则没有交集那么直接将现在的[st,ed]存入用于保存最后剩余区间的vector<pair<int,int>>中; 然后st=后一个区间.起点,ed=后一个区间;最后的那个区间是没法和后面比的,也要直接存入vector中
-
//法一,只算剩余区间个数
// #include<iostream>
// #include<algorithm>
// using namespace std;
// typedef pair<int,int> PII;
// const int N = 1e5+10;
// int n;
// PII a[N];
// int main()
// {
// cin>>n;
// for(int i=1;i<=n;i++){
// cin>>a[i].first>>a[i].second;
// }
// sort(a+1,a+n+1);
// //区间合并类问题,我们会维护一个区间 [st,ed]
// int ed=a[1].second,ans=1;
// for(int i=2;i<=n;i++){
// //新的区间和我们维护的区间有交集
// if(ed>=a[i].first) ed=max(ed,a[i].second);
// //新添加和区间和我们维护的区间没有交集,ans++,维护这个新添加的区间
// else ans++,ed=a[i].second;
// }
// cout<<ans<<endl;
// return 0;
// }
//法二,算区间个数 并维护合并后的区间情况
#include<iostream>
#include<algorithm>
using namespace std;
typedef pair<int,int> PII;
const int N = 1e5+10;
int n;
PII a[N];
vector<PII> res;
int main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i].first>>a[i].second;
}
sort(a+1,a+n+1);
int st=a[1].first,ed=a[1].second,ans=1;
for(int i=2;i<=n;i++){
if(ed>=a[i].first) ed=max(ed,a[i].second);
else{
res.push_back({st,ed});
ans++;
st=a[i].first,ed=a[i].second;
}
}
//最后一个[st,ed]的区间,也要合并到res;
res.push_back({st,ed});
cout<<ans<<endl;
// for(auto t:res){
// cout<<t.first<<" "<<t.second<<endl;
// }
return 0;
}
标签:int,
ed,
合并,
st,
离散,
second,
alls,
区间
From: https://www.cnblogs.com/zhouylove/p/17220239.html

