T1 涂色游戏
非常困难的题目，我们需要记录每一行/每一列最后一次被修改的时间以及被修改成什么颜色。
输出的时候每一个格子是受行影响还是列影响即可。复杂度 \(O(nm)\)。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int BS=1<<20|5;
char buf[BS],*P1,*P2;
inline char gc(){
if(P1==P2)P2=(P1=buf)+fread(buf,1,BS,stdin);
return P1==P2?EOF:*(P1++);
}
inline int in(){
int x=0,f=1;char ch=gc();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=gc();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=gc();
return x*f;
}
typedef pair<int,int> P;
const int N=1e5+5;
int n,m,q;
P a[N],b[N];
void solve(){
n=in(),m=in(),q=in();
for(int i=1;i<=n;i++)a[i]=make_pair(0,0);
for(int i=1;i<=m;i++)b[i]=make_pair(0,0);
for(int i=1;i<=q;i++){
int op=in(),x=in(),y=in();
if(!op)a[x]=make_pair(i,y);
else b[x]=make_pair(i,y);
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
printf("%d%c",max(a[i],b[j]).second,j==m?'\n':' ');
}
}
}
int main(){
freopen("paint.in","r",stdin);
freopen("paint.out","w",stdout);
int T=in();
while(T--)solve();
return 0;
}
T2 幂次
可以被写成 \(a^b\) 的不超过 \(n\) 的数很明显有 \(\lfloor n^{\frac 1 b} \rfloor\) 个，这个可以二分出来，记为 \(F(b)\)。但是答案很明显不是把所有 \(F\) 加起来（这样会算重）。为了不算重，我们记 \(G(b)\) 为 可以被写为 \(a^b\) 且不能被写成 \(a'^{b'},b'>b\) 的数的数量。这下每个数就只会贡献一次，答案就是 \(G\) 的和。然后考虑 \(F\) 和 \(G\) 的关系，不难发现 \(F(i)=\sum_{i|j} G(j)\)，于是我们把 \(G\) 容斥出来就行了。
时间复杂度 \(O(k \log n+k \log k)\)。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
inline int in(){
int x;
scanf("%d",&x);
return x;
}
ll n,k;
ll f[105];
ll pw(ll x,int k){
__int128 y=1;
for(int i=1;i<=k;i++){
y*=x;
if(y>n){y=n+1;break;}
}
return (ll)y;
}
ll calc(int k){
ll l=1,r=n,mid;
while(l<=r){
mid=l+r>>1;
if(pw(mid,k)<=n)l=mid+1;
else r=mid-1;
}
return l-2;
}
int main(){
freopen("power.in","r",stdin);
freopen("power.out","w",stdout);
cin>>n>>k;
ll ans=1;
for(int i=k;i<60;i++){
f[i]=calc(i);
}
for(int i=59;i>=k;i--){
for(int j=i+i;j<60;j+=i)f[i]-=f[j];
ans+=f[i];
}
cout<<ans<<endl;
return 0;
}
T3 圣诞树
我们需要发现关键性质：路径不会自交。发现这一性质以后，可以推出，我们路径的一段前缀对应在环上，一定是一段区间（如果不是一段区间，那么以后来填空的时候一定会自交），于是可以列出 dp 状态 \(f_{l,r,0/1}\)，表示当前的区间是 \(l,r\)，最后一步是在 \(l\) 还是 \(r\)。然后讨论是 \(l-1\) 还是 \(r+1\) 来转移，转移的时候记录前驱状态，就可以打印方案了。
那么如何证明路径不会自交呢？考虑基本的情况：只有四个点。
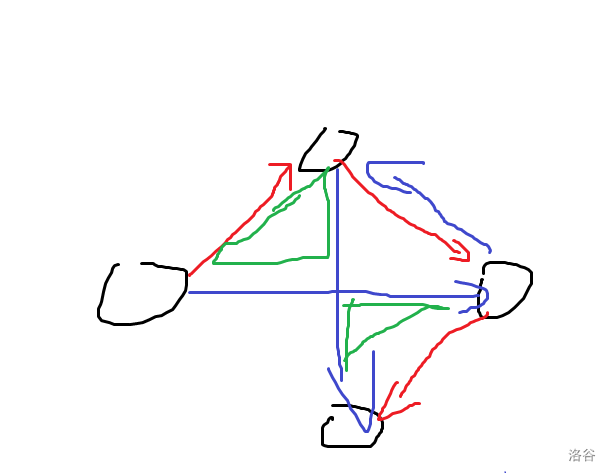style="zoom:50%;"
其中红色的路径不自交，蓝色的路径自交，两者不同的位置是两个绿色的三角形，由三角形两边之和大于第三边可得蓝色路径一定更长。
而点更多的情况一定可以归纳到若干四个点的基本情况，所以路径自交一定不优。
综上，直接区间 dp，复杂度 \(O(n^2)\)。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef double db;
inline int in(){
int x;
scanf("%d",&x);
return x;
}
const int N=1005;
int n,k;
db px[N],py[N];
db dis(int a,int b){
a%=n,b%=n;
return sqrt((px[a]-px[b])*(px[a]-px[b])+(py[a]-py[b])*(py[a]-py[b]));
}
pair<db,int> f[3005][3005][2];
int main(){
freopen("tree.in","r",stdin);
freopen("tree.out","w",stdout);
scanf("%d",&n);
db mx=-1e18;
for(int i=0;i<n;i++){
scanf("%lf%lf",px+i,py+i);
if(py[i]>mx)mx=py[i],k=i;
}
for(int i=0;i<3*n;i++)
for(int j=0;j<3*n;j++)
f[i][j][0]=f[i][j][1]=make_pair(1e18,0);
f[k+n][k+n][0]=make_pair(.0,0);
for(int d=1;d<n;d++){
for(int l=k+n,r=k+n+d-1;r>=k+n;l--,r--){
f[l-1][r][0]=min(f[l-1][r][0],make_pair(f[l][r][0].first+dis(l-1,l),0));
f[l-1][r][0]=min(f[l-1][r][0],make_pair(f[l][r][1].first+dis(l-1,r),1));
f[l][r+1][1]=min(f[l][r+1][1],make_pair(f[l][r][0].first+dis(r+1,l),0));
f[l][r+1][1]=min(f[l][r+1][1],make_pair(f[l][r][1].first+dis(r+1,r),1));
}
}
db mn=1e18;int id=0;
for(int l=k+1;l<=k+n;l++){
if(f[l][l+n-1][0].first<mn)mn=f[l][l+n-1][0].first,id=l<<1;
if(f[l][l+n-1][1].first<mn)mn=f[l][l+n-1][1].first,id=l<<1|1;
}
int l=id>>1,r=l+n-1,c=id&1;
vector<int> v;
while(l<=r){
int c1=f[l][r][c].second;
if(!c)v.push_back(l%n),l++;
else v.push_back(r%n),r--;
c=c1;
}
reverse(v.begin(),v.end());
for(int x:v)printf("%d ",x+1);puts("");
return 0;
}
T4 密码锁
\(k=1\)：直接输出 \(max-min\)。
\(k=2\) ：把每列的 \(min\) 放第一行，\(max\) 放第二行，可以发现这样一定不劣，然后直接计算答案。
对于 \(k=3,4\) 的情况，我们可以先二分答案，然后枚举每一行的 \(min\)，这下每行的区间都已确定，就可以 check 是否可行。这个暴力是自然的，复杂度 \(O((nk)^{k+1})\)。并不能拿到多少分，但是在此基础上，我们可以想到，必定有一行的 \(min\) 是全局 \(min\)，还有另外一行的 \(max\) 是全局 \(max\) （只有最坏的情况全局 \(min\) 和 \(max\) 会放在同一行）。我们钦定第一行是全局 \(min\)，然后枚举哪一行是全局 \(max\)，于是这样就有两行的区间确定了，我们只需要考虑剩下的 \(k-2\) 行。
当 \(k=3\) 相当于数轴上有若干个点，一共有 \(n\) 种颜色，问是否有一段长度为 \(mid\) 的区间可以覆盖所有颜色。可以直接双指针判断。
当 \(k=4\) 相当于二维平面上有若干个点，一共有 \(n\) 中颜色，问是否有一段大小为 \(mid \times mid\) 的矩形可以覆盖所有颜色。然后我们对 \(x\) 这一维双指针，然后对 \(y\) 这一维线段树。为了一种颜色不被算重，需要做一些特殊处理，在此就各显神通了。
复杂度 \(O(\sum n \log^2 n)\)。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int BS=1<<20|5;
char buf[BS],*P1,*P2;
inline char gc(){
if(P1==P2)P2=(P1=buf)+fread(buf,1,BS,stdin);
return P1==P2?EOF:*(P1++);
}
inline int in(){
int x=0,f=1;char ch=gc();
while(ch<'0'||ch>'9'){ch=gc();if(ch=='-')f=-1;}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=gc();
return x*f;
}
const int N=1e5+5,inf=1e9;
int n,k;
int a[N][4];
namespace solve1{
void main(){
n=in();
int mn=inf,mx=0;
for(int i=1;i<=n;i++){
a[i][0]=in();
mn=min(mn,a[i][0]);
mx=max(mx,a[i][0]);
}
printf("%d\n",mx-mn);
}
}
namespace solve2{
void main(){
n=in();
for(int j=0;j<2;j++)
for(int i=1;i<=n;i++)
a[i][j]=in();
int mn0=inf,mx0=0,mn1=inf,mx1=0;
for(int i=1;i<=n;i++){
if(a[i][0]>a[i][1])swap(a[i][0],a[i][1]);
mn0=min(mn0,a[i][0]),mx0=max(mx0,a[i][0]);
mn1=min(mn1,a[i][1]),mx1=max(mx1,a[i][1]);
}
printf("%d\n",max(mx0-mn0,mx1-mn1));
}
}
namespace solve3{
int mn,mx;
int cnt[N],buc[3];
bool check(int mid){
vector<pair<int,int> > v;
for(int i=1;i<=n;i++){
bool flag=0;
for(int j=0;j<3;j++){
if((a[i][(j+1)%3]>mn+mid||a[i][(j+2)%3]<mx-mid))continue;
v.push_back(make_pair(a[i][j],i));
}
}
sort(v.begin(),v.end());
int m=v.size();
for(int i=1;i<=n;i++)cnt[i]=0;buc[0]=n;
for(int l=0,r=0;r<m;l++){
for(;r<m&&v[r].first<=v[l].first+mid;r++){
int &x=cnt[v[r].second];buc[x]--,buc[++x]++;
}
if(!buc[0])return 1;
int &x=cnt[v[l].second];buc[x]--,buc[--x]++;
}
return 0;
}
bool check1(int mid){
if(check(mid))return 1;
for(int i=1;i<=n;i++)swap(a[i][0],a[i][1]);
return check(mid);
}
void main(){
n=in();
mn=inf,mx=0;
for(int j=0;j<3;j++)
for(int i=1;i<=n;i++){
a[i][j]=in();
mn=min(mn,a[i][j]);
mx=max(mx,a[i][j]);
}
int l=0,r=mx-mn,mid;
while(l<=r){
mid=l+r>>1;
if(check1(mid))r=mid-1;
else l=mid+1;
}
printf("%d\n",r+1);
}
}
namespace solve4{
int mn,mx;
struct node{
int x,y,id,pos;
};
vector<node> V;
vector<pair<int,int> > V1[N];
struct Snode{
int val,tag,lazy;
}T[N<<2];
#define val(x) T[(x)].val
#define tag(x) T[(x)].tag
#define lazy(x) T[(x)].lazy
inline void pushdown(int p){
if(!lazy(p))return;
lazy(p)=0;
lazy(p<<1)=1,lazy(p<<1|1)=1;
tag(p<<1)=0,tag(p<<1|1)=0;
val(p<<1)=0,val(p<<1|1)=0;
}
inline void pushup(int p){
val(p)=max(val(p<<1),val(p<<1|1));
val(p)+=tag(p);
}
void modify(int p,int l,int r,int ql,int qr,int v){
if(ql<=l&&r<=qr){
tag(p)+=v,val(p)+=v;
return;
}
pushdown(p);
int mid=l+r>>1;
if(ql<=mid)modify(p<<1,l,mid,ql,qr,v);
if(mid<qr)modify(p<<1|1,mid+1,r,ql,qr,v);
pushup(p);
}
bool mark[N][4];
inline int getpre(int x){
int pre=0;
int i=V[x].id;
for(int j=V[x].pos-1;j>=0;j--)
if(mark[i][j]){pre=V1[i][j].second;break;}
return pre;
}
inline int getnxt(int x){
int nxt=inf;
int i=V[x].id;
for(int j=V[x].pos+1;j<V1[i].size();j++)
if(mark[i][j]){nxt=V1[i][j].second;break;}
return nxt;
}
bool check(int mid,int X,int Y){
V.clear();
for(int i=1;i<=n;i++){
V1[i].clear();
for(int j=0;j<k;j++){
int p1=j,p2=(j+1+X)%4;
if(Y)swap(p1,p2);
if(a[i][p1]>mn+mid||a[i][p2]<mx-mid)continue;
V1[i].emplace_back(a[i][(j+2-X)%4],a[i][(j+3)%4]);
}
if(!V1[i].size())return 0;
sort(V1[i].begin(),V1[i].end(),[](pair<int,int> &a,pair<int,int> &b){return a.second<b.second;});
for(int j=0;j<V1[i].size();j++)
V.push_back({V1[i][j].first,V1[i][j].second,i,j});
}
for(int i=1;i<=n;i++)
for(int j=0;j<4;j++)
mark[i][j]=0;
sort(V.begin(),V.end(),[](node &a,node &b){return a.x<b.x;});
lazy(1)=1,tag(1)=0,val(1)=0;
for(int l=0,r=0;r<V.size();l++){
for(;r<V.size()&&V[r].x<=V[l].x+mid;r++){
mark[V[r].id][V[r].pos]=1;
int pre=getpre(r),nxt=getnxt(r);
int L=max(pre+1,V[r].y-mid),R=min(V[r].y,nxt-mid-1);
if(L<=R)modify(1,1,mx,L,R,1);
}
if(val(1)==n)return 1;
mark[V[l].id][V[l].pos]=0;
int pre=getpre(l),nxt=getnxt(l);
int L=max(pre+1,V[l].y-mid),R=min(V[l].y,nxt-mid-1);
if(L<=R)modify(1,1,mx,L,R,-1);
}
return 0;
}
bool check1(int mid){
if(check(mid,0,0))return 1;
if(check(mid,0,1))return 1;
return check(mid,1,1);
}
void main(){
n=in();
mn=inf,mx=0;
for(int j=0;j<4;j++)
for(int i=1;i<=n;i++){
a[i][j]=in();
mn=min(mn,a[i][j]),mx=max(mx,a[i][j]);
}
int l=0,r=mx-mn,mid;
while(l<=r){
mid=l+r>>1;
if(check1(mid))r=mid-1;
else l=mid+1;
}
printf("%d\n",r+1);
}
}
int main(){
freopen("lock.in","r",stdin);
freopen("lock.out","w",stdout);
int T=in();k=in();
if(k==1)while(T--)solve1::main();
if(k==2)while(T--)solve2::main();
if(k==3)while(T--)solve3::main();
if(k==4)while(T--)solve4::main();
return 0;
}