二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]
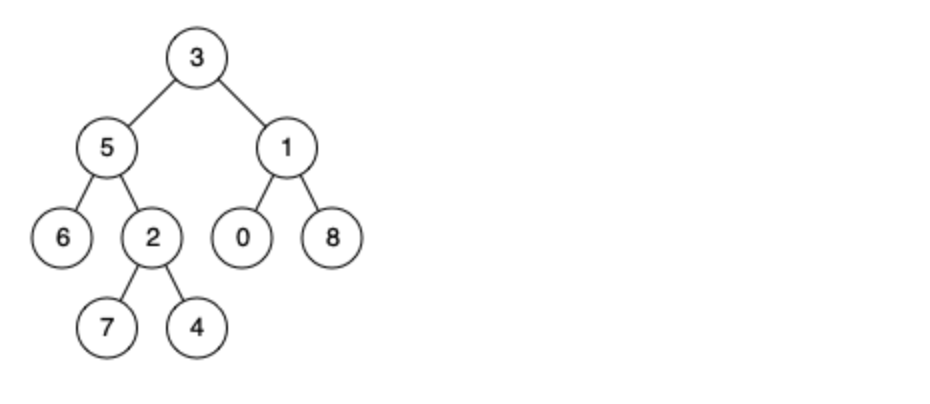
示例 1: 输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 输出: 3 解释: 节点 5 和节点 1 的最近公共祖先是节点 3。
示例 2: 输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4 输出: 5 解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。
说明:
- 所有节点的值都是唯一的。
- p、q 为不同节点且均存在于给定的二叉树中
思路
根据题目要求,我们需要先找到对应的两个节点p、q,然后再回去找他们的最近的公共父节点
这么一个过程实际上顺序是自下而上的,也就是说,如果能从下往上搜索父节点,那么这个问题就好解决了,如何做到呢?
首先,节点p、q肯定是左右节点,那么我们遍历的时候肯定得先遍历到这两个左右节点
符合上述条件的遍历方式是:后序遍历(左右中)
其次,当找到节点p、q,我们需要"回头"往上找他们的公共父节点,实际上就可以在左右中的 中 里面处理查找公共父节点的逻辑
后序遍历也满足查找父节点的要求
判断公共祖先
遍历方式确定了,那么还需要解决一个问题:怎么判断一个节点是不是节点q和节点p的公共祖先?
这里一共有两种情况:
情况1
最容易想到的是第一种,即当遍历到某个节点A,其左子节点B找到p(并返回),右子节点C找到q(并返回),那么此时可以认为节点A是B、C的最近公共祖先
图示如下:

从根节点6开始进行后序遍历,那么先遍历6的左子节点4和右子节点7
(先进入左子节点4的递归中)
到4之后,因为其左右子节点不为空,使用又继续按后序顺序遍历
此时在4的左子节点找到了p,返回
在4的右子节点找到了q,返回
然后再p、q的父节点4这里处理逻辑:找到目标节点,当前根节点4为最近公共节点
于是把4往根节点6传
最后的效果就是:在递归函数中输入了一颗二叉树的根节点6,然后通过递归找到了目标节点p、q,然后通过后序遍历左右中的顺序在 中 里面处理了最近公共父节点的判断逻辑,并把处理所得的最近公共父节点通过回溯传到递归的第一层,得到结果
情况2

还是从根节点6开始,只不过这次我们在6的左子节点就找到了q
因为还没有找到p,并且节点4还有子节点,所以还得继续遍历(只要没有找齐p、q都应该继续遍历,因此在该问题中,我们可能被迫需要遍历整颗二叉树而不是找到目标值就返回)
继续
遍历节点4的左右子节点,在左子节点找到p,并且其没有子节点,此时需要返回
在节点4的位置处理其左右子节点返回的结果,并给出当前p、q的最近公共父节点(具体操作在代码里再解释),实际上就是节点4
于是我们得到了p、q的最近公共父节点,此时将结果往上返回,得出最后的解
总结
通过分析两种情况,可以发现:不论p、q以哪种方式被找到,最终的处理过程都在左右中顺序里面的 中 的位置处理。(也就是调用递归函数时输入的节点。从递归函数的角度讲,该节点为根节点;从我们遍历的角度讲,该节点为当前节点,也就是左右中里面位于 中 的节点)
因此,情况2会被情况1包含,在处理情况1的逻辑下,情况2会被一并处理
代码分析
还是写递归的老一套
1、确定递归函数参数和返回值
首先能够确定的是,这里的递归函数需要返回值,因为我们需要通过返回值来了解是否找到了p、q
一种直接的想法是返回bool值,但是不行
因为在中节点位置完成逻辑处理后,我们需要返回的是 最近公共父节点 ,这是一个节点类型值
所以干脆直接就设定返回值为节点类型,如果有返回值就表明找到p或q
这样的话还可以利用解题模板
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
}
};
2、确定终止条件
根据上面的分析,递归结束的情况有:
- 当找到p
- 找到q
- 当前输入的节点root为NULL
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(root == p || root ==q || root == NULL) return root;
}
};
如果 root == q,或者 root == p,说明找到 q p ,则将其返回,这个返回值,后面在中节点的处理过程中会用到
3、确定单层处理逻辑
因为本题中需要使用回溯机制来处理返回值,而后序遍历的顺序是 左右中
我们是在中节点位置处理父节点判断逻辑的,但是由于是先遍历 左右 节点
因此在得到返回值并处理之前,需要等待左右节点的递归遍历完成,而递归一旦触发,就会一直遍历下去直到递归函数的输入为NULL,也就是遇到叶子节点才会结束
因此,在本题中,由于使用了后序遍历,我们被迫遍历了整颗二叉树
根据在路径总和问题中的讨论有提到这种情况
题外话
如果递归函数有返回值,如何区分要搜索一条边,还是搜索整个树呢?
搜索一条边的写法:
if (递归函数(root->left)) return ;
if (递归函数(root->right)) return ;
搜索整个树写法:
left = 递归函数(root->left); // 左
right = 递归函数(root->right); // 右
left与right的逻辑处理; // 中
上面两种写法的区别是:
搜索一条边时,我们遇到不符合条件的节点时就立马返回,然后换边搜索
搜索整个树时,我们使用一个变量去接收递归函数的返回值(是的,根据规则搜索整棵树时一般有返回值),然后在中节点处进行逻辑处理,并通过回溯返回到上一级递归
这也是为什么会"被迫"遍历整颗树的原因
言归正传
现在可以按照后序遍历顺序去写处理逻辑了
class Solution {
public:
//确定递归函数的输入和返回值
//因为需要通过返回值,在中节点位置判断父节点,且需要返回父节点值,故返回值应该是节点类型
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
//确定终止条件
//当以下条件满足时,都要返回当前节点
if(root == NULL || root == q || root == p) return root;
//确定单层处理逻辑
//后序遍历
//左
TreeNode* left = lowestCommonAncestor(root->left, p, q);
//右
TreeNode* right = lowestCommonAncestor(root->right, p, q);
//中,在中节点位置处理左右的返回值,判断当前节点是否为最近公共父节点
//如果当前节点的左右子节点的返回值都不为空
//表明找到目标值,那么当前节点即为最近公共父节点
if(left != NULL && right != NULL) return root;
if(left == NULL && right != NULL){//左节点不为空右为空,说明当前节点不是公共父节点,把left再往上传(回溯)
return right;
}else if(left != NULL && right == NULL){//右节点不为空左为空,说明当前节点不是公共父节点,把right再往上传(回溯)
return left;
}else{// (left == NULL && right == NULL)
return NULL;//什么都没找到返回空
}
}
};
注意,这里我们是使用回溯过程中返回的值来判断公共父节点的
当前节点调用递归函数后,通过递归我们会寻找其下所有子节点中p、q存在的位置(题目说了必定存在,且不会是重复值)
当找到之后递归函数会通过回溯机制层层返回p、q
假如出现以下情况:(p、q不在同一分支)

这种情况的话,虽然不能马上找到最近公共父节点,但是通过层层递归并回溯p、q的值,总会在满足最近公共父节点的节点处触发条件
如果是代码分析中的情况1,那么返回一次就遇到了它们的最近公共父节点
如果是代码分析中的情况2,或者p、q距离比较远,那么就继续回溯返回呗,反正如果都找不到这个满足条件的公共父节点,那最后的最近公共父节点就是最开始调用递归的那个节点,也就是根节点
标签:遍历,16,递归函数,节点,二叉树,公共,返回值,root,LeetCode From: https://www.cnblogs.com/DAYceng/p/17174409.html