问题描述
在 x 轴上有一个一维的花园。花园长度为 n,从点 0 开始,到点 n 结束。
花园里总共有 n + 1 个水龙头,分别位于 [0, 1, ..., n] 。
给你一个整数 n 和一个长度为 n + 1 的整数数组 ranges ,其中 ranges[i]
(下标从 0 开始)表示:如果打开点 i 处的水龙头,可以灌溉的区域为 [i - ranges[i], i + ranges[i]] 。
请你返回可以灌溉整个花园的 最少水龙头数目 。如果花园始终存在无法灌溉到的地方,请你返回 -1 。
示例 1:
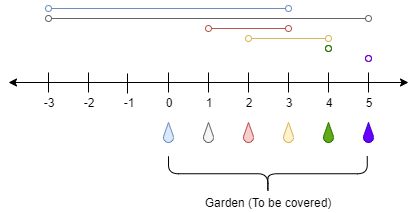
输入:n = 5, ranges = [3,4,1,1,0,0]
输出:1
解释:
点 0 处的水龙头可以灌溉区间 [-3,3]
点 1 处的水龙头可以灌溉区间 [-3,5]
点 2 处的水龙头可以灌溉区间 [1,3]
点 3 处的水龙头可以灌溉区间 [2,4]
点 4 处的水龙头可以灌溉区间 [4,4]
点 5 处的水龙头可以灌溉区间 [5,5]
只需要打开点 1 处的水龙头即可灌溉整个花园 [0,5] 。
示例 2:
输入:n = 3, ranges = [0,0,0,0]
输出:-1
解释:即使打开所有水龙头,你也无法灌溉整个花园。
提示:
1 <= n <= 10⁴ranges.length == n + 10 <= ranges[i] <= 100
解题思路
贪心
假设当前能浇灌的最右端为end,对应的水龙头为start_idx,那么应该选满足start[i] <= end且end[i]最大的i。在这里,我们构建一个数组vector<int> right_most(n + 1, 0),表示当坐标i的点能被浇灌到时,所能浇灌到的最远点。
然后,我们从0~n遍历i,如果right_most[i]大于next_right,那么更新next_right,原先的next_right记为cur_right,如果i == cur_right了,说明要再开一个水龙头。
排序+二分查找
这个做法也是有一点贪心的思路,假设当前能浇灌的最右端为end,对应的水龙头为start_idx,那么应该选满足start[i] <= end且end[i]最大的i,可以利用二分查找找到满足start[i] <= end的i的最大值idx,然后遍历[start_idx, idx],找最大的end[i],并更新start_idx。
动态规划
dp[i]表示覆盖[0, i]所需要的最少水龙头数量;
我们假设dp[i]的情况下,打开的最后一个水龙头为(start[j], end[j]),那么对于start[j] < k < end[j],dp[k] = min(dp[k], dp[start[j]] + 1),所以这里我们需要将dp[i]初始化为一个极大值,并且需要将water_range数组按照start[i]从小到大排序。
代码
动态规划
class Solution {
public:
int minTaps(int n, vector<int> &ranges) {
vector<vector<int>> water_range;
for (int i = 0; i <= n; i++) {
water_range.push_back({std::max(0, i - ranges[i]), std::min(i + ranges[i], n)});
}
std::sort(water_range.begin(), water_range.end());
vector<int> dp(n + 1, 30000);
dp[0] = 0;
for(int i = 0; i <= n; i++) {
if (dp[water_range[i][0]] == 30000)
return -1;
for (int j = water_range[i][0]; j <= water_range[i][1]; j++) {
dp[j] = std::min(dp[j], dp[water_range[i][0]] + 1);
}
}
return dp[n];
}
};
贪心
class Solution {
public:
int minTaps(int n, vector<int> &ranges) {
int right_most[n + 1]; memset(right_most, 0, sizeof(right_most));
for (int i = 0; i <= n; ++i) {
int r = ranges[i];
if (i > r) right_most[i - r] = i + r; // 对于 i-r 来说,i+r 必然是它目前的最大值
else right_most[0] = max(right_most[0], i + r);
}
int ans = 0;
int cur_right = 0; // 已建造的桥的右端点
int next_right = 0; // 下一座桥的右端点的最大值
for (int i = 0; i < n; ++i) { // 注意这里没有遍历到 n,因为它已经是终点了
next_right = max(next_right, right_most[i]);
if (i == cur_right) { // 到达已建造的桥的右端点
if (i == next_right) return -1; // 无论怎么造桥,都无法从 i 到 i+1
cur_right = next_right; // 造一座桥
++ans;
}
}
return ans;
}
};
排序+二分查找
class Solution {
public:
// 二分查找
int Bfind(vector<vector<int>> &vec, int target, int start_idx) {
int left = start_idx, right = vec.size();
int mid = left + (right - left) / 2;
while (left < right) {
if (vec[mid][0] < target) {
left = mid + 1;
} else {
right = mid;
}
mid = left + (right - left) / 2;
}
return left;
}
int minTaps(int n, vector<int> &ranges) {
vector<vector<int>> water_range;
for (int i = 0; i <= n; i++) {
water_range.push_back({i - ranges[i], i + ranges[i]});
}
auto cmp = [&](vector<int> &v1, vector<int> &v2) {
if (v1[0] == v2[0])
return v1[1] <= v2[1];
return v1[0] < v2[0];
};
std::sort(water_range.begin(), water_range.end(), cmp);
int start_idx = 0, end = 0;
int cnt = 0;
while (end < n) {
int idx = Bfind(water_range, end + 1, start_idx) - 1; // 找到满足start[idx] <= end的最大的idx
for (int i = start_idx; i <= idx; i++) {
if (water_range[i][1] > end) {
start_idx = i;
end = water_range[i][1];
}
}
cnt++;
if (cnt > n)
return -1;
}
return cnt;
}
};