【LeetCode二叉树#09】路径总和I+II（回溯回溯，还是™的回溯）

标签：node count 路径 09 right 二叉树 回溯 节点 left

路径总和

力扣题目链接(opens new window)

给定一个二叉树和一个目标和，判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和。

说明: 叶子节点是指没有子节点的节点。

示例: 给定如下二叉树，以及目标和 sum = 22，

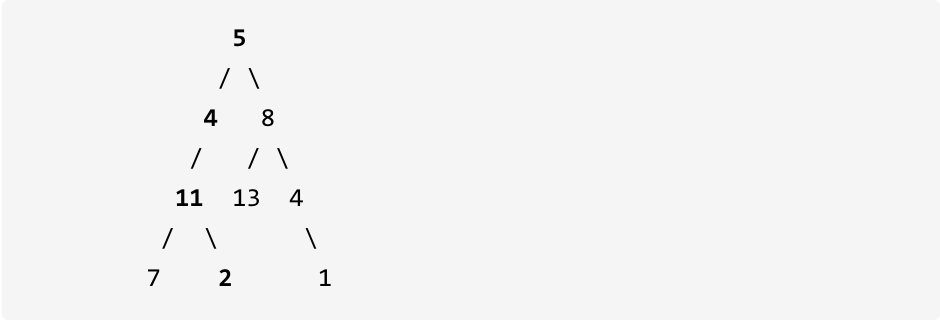
返回 true, 因为存在目标和为 22 的根节点到叶子节点的路径 5->4->11->2

思路

用递归的方法做，传入target值，没遍历到一个节点就与其做差

如果最后遍历到叶子节点时target值变成0，那么就说明本条路径的节点之和满足target值

递归法

1、确定递归函数参数和返回值

输入肯定是根节点了，因为还需要把target传入，所以还需要一个计数变量int count

那么，返回值如何确定？或者说需不需要返回值？

这里引申一个问题：递归函数什么时候需要返回值？

可以总结为如下三点：

• 如果需要搜索整棵二叉树且不用处理递归返回值，递归函数就不要返回值。（113.路径总和ii）
• 如果需要搜索整棵二叉树且需要处理递归返回值，递归函数就需要返回值。 （236. 二叉树的最近公共祖先 (opens new window)）
• 如果要搜索其中一条符合条件的路径，那么递归一定需要返回值，因为遇到符合条件的路径了就要及时返回。（本题的情况）

因为题目只要求我们找出一条符合路径值等于target的路径，所以我们有可能不需要完整遍历整颗二叉树。且一旦找到满足条件的路径，需要及时返回

因此递归函数的返回值应该是bool

bool traversal(TreeNode* node, int count){
    
}

2、确定终止条件

这里要考虑如何统计全部路径节点的值

注意，不要使用累加的方式（即遍历一个节点加一个，然后最后再判断是否满足target），这种方式虽然很容易想到，但是代码实现比较麻烦

因此，我们将count设置为target的大小，让其在递归遍历的过程中递减

那么结束的条件就有以下两种：

1、遇到叶子节点（遍历结束），且当前count已经递减至0

2、遇到叶子节点（遍历结束）但count不为0

bool traversal(TreeNode* node, int count){
    if(node->left == NULL && node->right == NULL && count == 0) return true;
    if(node->left == NULL && node->right == NULL) return false;
}

3、确定单层处理逻辑

调用递归函数，当我们找到满足条件的路径或者已经到达叶子节点后，需要通过回溯将count值再加回原来的初值状态（等于target）

因为递归函数设置了返回值，如果我们找到符合条件的路径，就可以立刻返回true

没找到就返回false

bool traversal(TreeNode* node, int count){
    //确定终止条件
    //到叶子节点并找到路径
    if(node->left == NULL && node->right == NULL && count == 0) return true;
    //到叶子节点但没找到路径
    if(node->left == NULL && node->right == NULL) return false;
    
    //确定单层处理逻辑
    //调用递归函数
    if(node->left){
       count -= node->left->val;//不断递减
       //如果递归函数返回true，则找到路径，可以直接返回true
       if(traversal(node->left, count)) return true;
          count += node->left->val;//回溯，撤销处理结果
       }
    if(node->right){
       count -= node->right->val;//不断递减
       //如果递归函数返回true，则找到路径，可以直接返回true
       if(traversal(node->right, count)) return true;
         count += node->right->val;//回溯，撤销处理结果
       }
       return false;//没找到返回false
}

代码

class Solution {
public:
    //使用递归，遍历出所有路径，将路径之和与target比较
    //确定递归函数的参数和返回值
    bool traversal(TreeNode* node, int count){
        //确定终止条件
        //到叶子节点并找到路径
        if(node->left == NULL && node->right == NULL && count == 0) return true;
        //到叶子节点但没找到路径
        if(node->left == NULL && node->right == NULL) return false;

        //确定单层处理逻辑
        //调用递归函数
        if(node->left){
            count -= node->left->val;//不断递减
            //如果递归函数返回true，则找到路径，可以直接返回true
            if(traversal(node->left, count)) return true;
            count += node->left->val;//回溯，撤销处理结果
        }
        if(node->right){
            count -= node->right->val;//不断递减
            //如果递归函数返回true，则找到路径，可以直接返回true
            if(traversal(node->right, count)) return true;
            count += node->right->val;//回溯，撤销处理结果
        }
        return false;//没找到返回false

    }
    bool hasPathSum(TreeNode* root, int targetSum) {
        if (root == NULL) return false;//先判断根节点是否为空
        int count = targetSum - root->val;//根节点也算在路径中，所以count也要减去其值
        return traversal(root, count);
    }
};

迭代法

TBD

注意点

1、在主函数中，必须确认根节点是否为空，否则必错

2、在主函数中，不要忘记把根节点的值加入递减计数

路径总和II

力扣题目链接(opens new window)

给定一个二叉树和一个目标和，找到所有从根节点到叶子节点路径总和等于给定目标和的路径。

说明: 叶子节点是指没有子节点的节点。

示例: 给定如下二叉树，以及目标和 sum = 22，

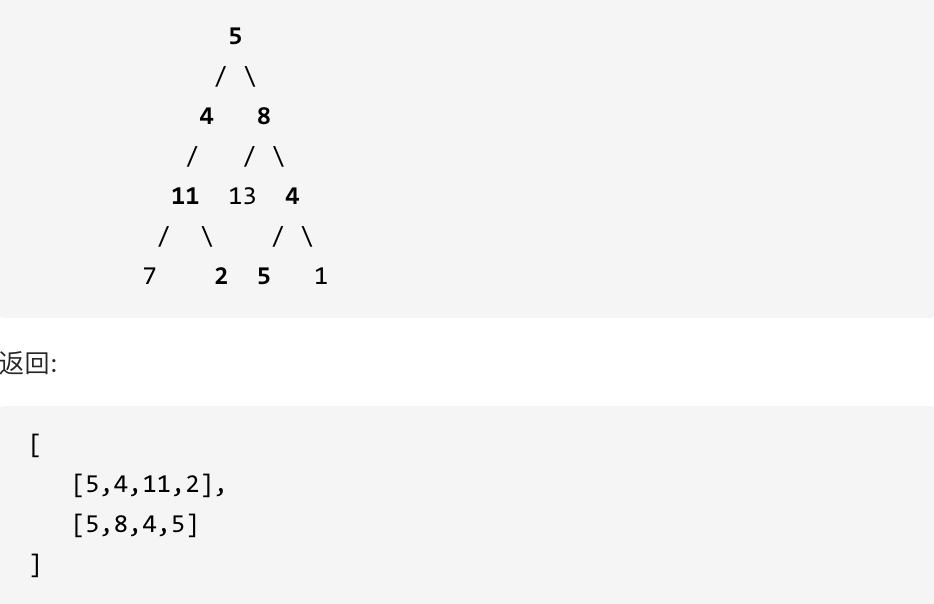
思路

因为题目要求的是返回所有路径节点和满足target的路径

所以，我们需要遍历整棵树

按照前面的讨论，这种情况下，递归函数不需要返回值（因为不需要满足条件就返回）

这里只介绍递归法，迭代法太麻烦了，写了也记不住

本题中，用于存放路径的数组path和存放结果的二维数组res需要定义在递归函数外

1、确定递归函数的参数和返回值

与路径总和的基本思路一致，输入是根节点和一个计数变量（通过递减来寻找满足条件的路径）

返回值是不需要的

2、确定终止条件

终止条件也与路径总和一致，共两种：

• 遇到叶子节点，且路径满足条件
• 遇到叶子节点但不满足条件

3、确定单层逻辑

在这一步中，我们除了对计数变量count进行递减和回溯，还需要将当前节点的值加入路径数组path中，并在回溯时将元素pop掉

代码

class Solution {
public:
    vector<vector<int>> res;//存放最值输出结果
    vector<int> path;//存放当前满足条件的路径
    //确定递归函数的参数和返回值
    //输入参数为根节点和计数变量
    //本题中，需要找出所有路径节点之和满足条件的路径，因此需要遍历整棵树，故没有返回值
    void traversal(TreeNode* node, int count){
        //确定终止条件
        //遇到叶子节点，且路径满足条件
        if(node->left == NULL && node->right == NULL && count == 0){
            //保存此时path中记录的路径
            res.push_back(path);
            return;
        }
        //遇到叶子节点但不满足条件
        if(node->left == NULL && node->right == NULL) return;

        //确定单层逻辑
        if(node->left){
            //保存当前节点值到path
            path.push_back(node->left->val);
            //计数递减
            count -= node->left->val;
            traversal(node->left, count);//调用递归
            //回溯，包括计数变量和路径数组
            count += node->left->val;
            path.pop_back();
        }

        if(node->right){
            //保存当前节点值到path
            path.push_back(node->right->val);
            //计数递减
            count -= node->right->val;
            traversal(node->right, count);//调用递归
            //回溯，包括计数变量和路径数组
            count += node->right->val;
            path.pop_back();
        }
    }

    vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
        //确认根节点不为空
        if(root == NULL) return res;
        int count = targetSum - root->val;//将根节点加入递减计数
        path.push_back(root->val);//将根节点值加入数组
        traversal(root, count);
        return res;
    }
};

注意点

1、用于存放路径的数组path和存放结果的二维数组res需要定义在递归函数外

2、在主函数中，必须确认根节点是否为空

3、在主函数中，不要忘记把根节点的值加入递减计数，以及路径数组

标签：node,count,路径,09,right,二叉树,回溯,节点,left
From： https://www.cnblogs.com/DAYceng/p/17156769.html