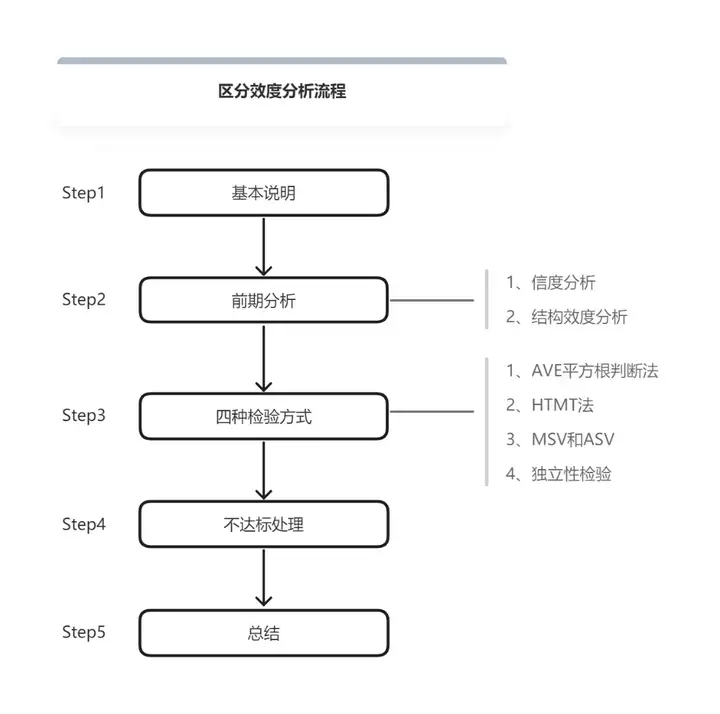
- 基本说明
区分效度(又称判别效度、区别效度),其实质也是一种结构效度。区分效度强调本不应该在同一因子的测量项,确实不在同一因子下面。比如说,测量项A和 B分别测量两个属性,应该分属于因子A和因子B中,如果确实是这样,那么说明区分效度很高;但是如果二者属于同一因子下,则说明区分效度不明显,量表设计的不好。 - 前期分析
进行区分效度的分析之前,应该已经完成量表的信度分析和结构效度分析。保证量表具有很高的可信度和良好的结构效度。
例如:现在有一份量表题,要对A1~A4,B1~B4,C1~C3,D1~D3,共14个量表题,进行信度和结构效度分析。
1.信度分析
信度用于衡量样本回答是否可靠,即样本有没有真实作答量表类题目。信度分析常见的衡量指标是克隆巴赫信度系数(Cronbach α系数值)。Cronbach α系数值如果在0.8以上,说明量表的信度非常高;如果在0.7以上,说明量表信度可以接受;如果在0.6以上,说明量表应该进行修正,但仍不失其价值;如果低于0.6则需要重新进行量表设计。
在SPSSAU系统中进行信度分析,因为共ABCD四个维度,所以分别进行四次信度分析后,得到各维度的α系数值,汇总如下表:
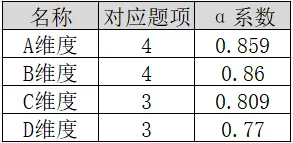
从上表可以看出,ABCD四个维度的α系数值均高于0.7,因而说明本次数据的信度质量水平较好,研究数据真实可靠。
2.结构效度分析
结构效度是为了分析“从量表获得的结果与设计该量表时所假定的理论之间的符合程度”。简单来讲,在研究者设计量表之初,一般会预设好几个维度,在经过因子分析后,需要验证测量的数据是否与预设的几个维度相对应,如果测量项与预设维度之间对应关系良好,则说明量表的结构效度良好,说明量表设计的合理且有效,那么通过该量表得到的分析结果也是有效的。
进行结构效度分析,最终因子与测量项对应关系良好,如下图:
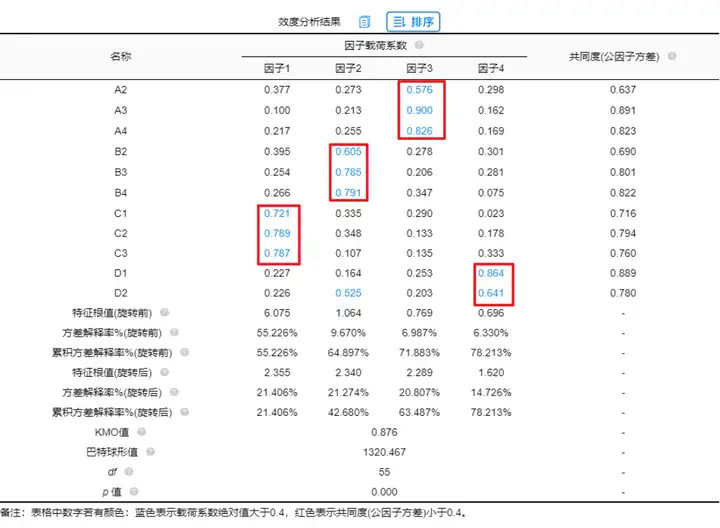
从效度分析结果看,A2~A4对应在因子3下;B2~B4对应在因子2下;C1~C3对应在因子1下;D1~D2对应在因子4下。对应关系良好,KMO值为0.876,且通过巴特球性检验说明量表结构效度良好。
- 四种检验方式
区分效度,在SPSSAU系统中,区分效度检验是使用验证性因子分析进行的。将各维度分别放进分析框中,进行分析,操作如下图:
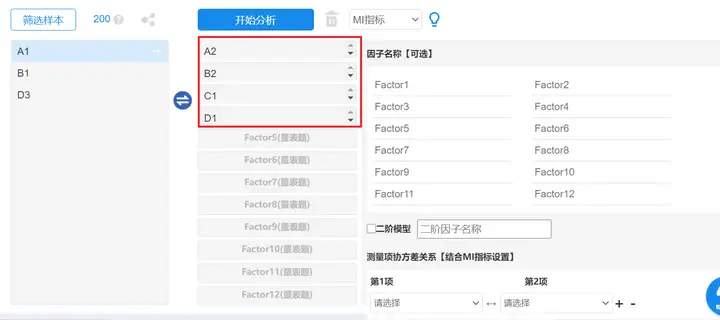
得到的分析结果中,区分效度检验共有四种检验方法,下面将一一进行说明。
- AVE平方根判断法
当每个因子的AVE平方根值均大于“该因子与其他因子的相关系数的最大值”,此时说明具有良好的区分效度。
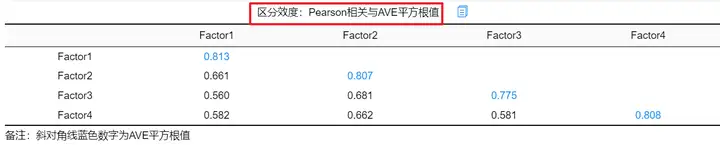
表格中斜对角线为AVE平方根值,其余值为相关系数。针对Factor1,其AVE平方根值为0.813,大于因子间相关系数绝对值的最大值0.661,意味着其具有良好的区分效度;同理,其他因子的区分效度都良好,意味着此次分析的量表具有良好的区分效度。
- HTMT法
HTMT(heterotrait-monotrait ratio)异质-单质比率,也就是特质间相关与特质内相关的比率。他是不同构面间指标相关的均值相对于相同构面间指标相关的均值乘积的开方的比值。如果HTMT值小于0.85(有时以0.9作为标准),则说明该两因子之间具有区分效度。

从HTMT分析结果来看,所有的HTMT值均小于0.85,意味着因子之间均有良好的区分度,量表的区分效度良好。
- MSV和ASV
MSV和ASV这两个指标也可用于区分效度判断;当MSV值小于AVE的值,并且ASV值小于AVE值则说明具有区分效度。

从上表可以看出,大部分因子的MSV值和ASV值都不小于AVE值,说明因子之间的区分效度并不好,进而量表的区分效度也比较差。
注意:不同的区分效度检验方法得到的检验结果可能不同。例如上述例题中三种检验区分效度的方式,得到的检验结果就不相同。此时,一般情况下只要有一种检验方式能够说明量表的区分效度良好,就可以认为量表有比较好的区分效度了。并不要求每种检验方式都要通过,才能认为区分效度良好。
- 独立性检验
独立性检验法需要研究者自行设置多个不同的CFA模型,然后对比不同的CFA模型拟合指标效果情况,并且判断得出最佳的模型,用于证明模型间的独立性情况。比如下表格:
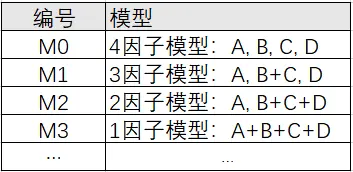
比如:本次量表共有4个因子A/B/C/D,默认将量表分为4个因子即上图中的M0模型。如果想知道这种模型是否最优,则可以通过对比不同的模型结构进行判断。例如上图中的M1模型,将因子A放在一个因子框中,因子B和因子C放在另一个因子框中,因子D放在另一个因子框中,再进行验证性因子分析,操作如下图:

同理,可以换成M2或M3等其他模型进行分析,将每次的模型拟合指标整理成下表,进行对比分析,找到最优模型。
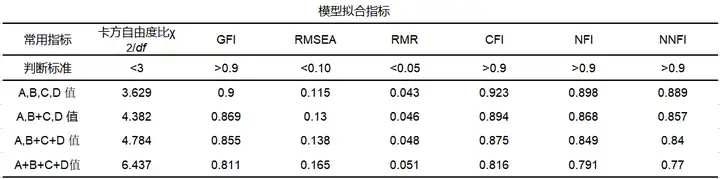
模型拟合指标用于整体模型拟合效度情况分析;通常情况下,拟合指标很多,指标很难全部达标;所以研究者可以根据实际情况,关注一些常用指标,包括卡方自由度比,GFI,RMSEA,RMR,CFI,NFI和NNFI。
从上表可以看出,对比分析以上7个指标,M0模型都是最接近判断标准的,即将因子分为A,B,C,D 4个的模型是最优的模型。
- 不达标处理
如果区分效度不达标,可以参考以下几个角度进行调整。
- 规范分析流程
一定要按照标准的分析流程进行区分效度分析,在进行区分效度之前要确保量表通过信度分析,并且具有良好的结构效度,这是进行区分效度的前提条件;量表的可靠性是有效性的必要前提;并且结构效度分析,要确保因子与测量项之间具有良好的对应关系。如果没有按照标准的分析流程进行分析,很有可能不能得到良好的区分效度。 - 尽量使用经典量表
经典量表是反复经过测试的,信度效度都很高,一般不会出问题。但是要注意经典量表与自己研究内容的契合度,即选择的经典量表是否适合研究自己的课题。 - 删除载荷系数法
删除载荷系数值比较低的测量项。
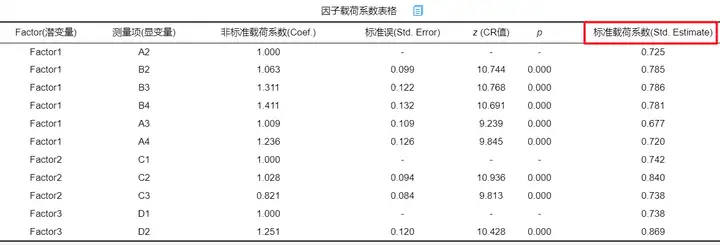
因子载荷系数值的统计意义就是变量i与公共因子(维度)j的相关系数(程度),绝对值越接近1,说明变量与公共因子的关系越密切。所以可以将载荷系数低的项(比如小于0.6)进行删除后,再进行分析。
- 模型修正
通常结合MI指标进行模型修正,建立协方差关系等。
MI值是一个模型调整指标,一般对模型调整时,可考虑多次尝试对比选择最优模型。比如设置MI>10时进行模型调整,操作如下图:
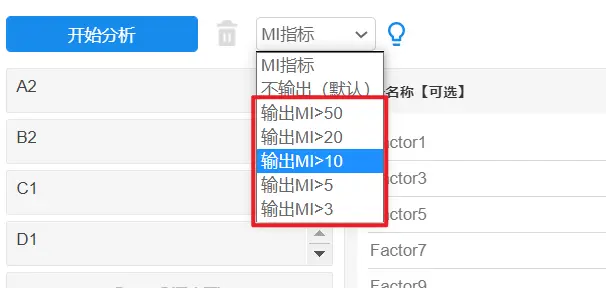
选择输出MI值后,再进行分析,此时SPSSAU输出因子和测量项-MI指标与测量项间MI指标两个表。
表1:因子和测量项-MI指标

上表为因子和测量项-MI指标,MI值并不固定判断标准,一般该值如果大于20说明关联性很强。从上可以看出,A2与Factor2、Factor3、Factor4这三个因子之间的MI值均大于20,说明A2与3个因子之间可能有较强的关联性。所以可以考虑将A2指标从模型中删除后,再次进行分析。
删除A2指标后,对比模型拟合指标整理如下:

从模型拟合指标来看,删除A2后,各项指标都更接近判断标准,说明使用MI指标进行模型修正是有效果的。
表2:测量项间MI指标值

测量项(显变量)间的MI指标,可用于辅助查看(或重新建立模型)测量项间的关系情况;如果MI值较大(比如大于20),说明该两个测量项间有着较强的关系,可考虑对它们建立协方差关系后再次分析。从上表可以看出,A4与A3之间的MI值大于20,说明二者之间有较强的关系,可以建立协方差关系,操作如下图:
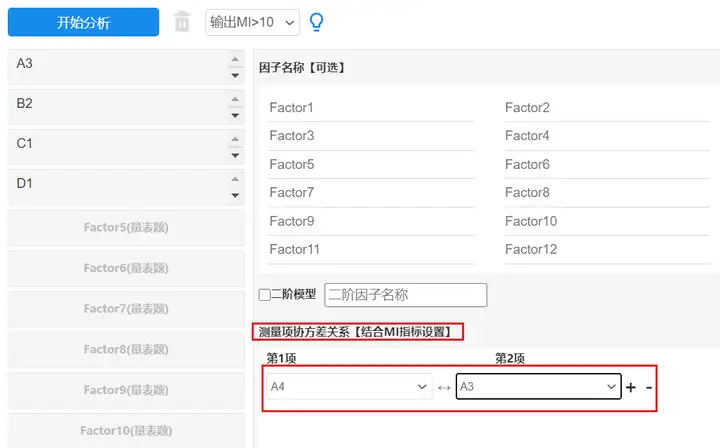
建立A4与A3之间协方差关系后,对比模型拟合指标如下:

从模型拟合指标来看,建立协方差关系后,各项模型拟合指标都更接近判断标准,说明通过观察MI指标建立协方差关系进行模型修正是有效果的。
- 其他
区分效度分析并没有指定的检验方法,上述4种检验方法如果有一个通过区分效度检验即可说明研究量表的区分效度良好,并不需要所有检验方法都通过。多种方法对比选择后进行说明即可。
- 总结
区分效度用于分析本不应该在同一因子下的测量项确实不在一个因子下。在进行区分效度分析之前需要先进行信度分析与结构效度分析,确保量表具有很高的可信度和良好的结构效度。在SPSSAU系统中,共提供4种区分效度的检验方法,分别是AVE平方根判断法、HTMT法、MSV和ASV判断法和独立性检验法。一般来讲4种分析方法有一种通过即可认为量表区分效度良好。如果区分效度检验不通过,可以进行不达标处理,包括规范分析流程、尽量使用经典量表、删除载荷系数低的测量项、进行模型修正等。
标签:分析,量表,流程,区分效度,因子,效度,模型 From: https://www.cnblogs.com/spssau/p/17152804.html