题意
对于一个元素个数大于 \(1\) 的可重集,每次取出两个数 \(x,y\) 合并。若 \(x\le y\le 2x\),则称其为危险合并。重复上述操作至无法合并。
给你一个初始为空的可重集与 \(n\) 次操作,每次加入或删除一个数,求每次操作后最大的危险合并次数。
\(1\le n \le5\times10^5,1\le x\le10^9\)。
题解
这题太妙了。深深感觉自己的弱小……
首先我们证明一个结论:每次取最小的两个数合并,可以取得最大的危险合并次数。方便起见,称 \(x,y\) 是危险合并为 \(x,y\) 合法。
设最小两值为 \(a,b\)。若不合并 \(a,b\),那么 \(a,b\) 中先与其他数合并的那个,不妨设为 \(b\)。考虑 \(b,c\) 合并,其中 \(c\geq b\):
- 若 \(b,c\) 合法。若 \(a+b\le c\),则显然 \(a+b,c\) 合法。若 \(a+b>c\),由 \(a\le c,b\le c\),有 \(a+b\le2c\),则 \(a+b,c\) 也合法。那么贪心先合并 \(a,b\)。
- 若 \(b,c\) 不合法。因为 \(2b<c\),所以 \(a+b<c\)。显然先合并 \(a,b\) 不会更劣。
于是不带修直接用小根堆即可。那么带修呢?
再证明一个结论:若最小二值 \(a,b\) 合法,则接下来的所有合并 \(x,y\),若 \(x,y\in[b,a+b]\),则 \(x,y\) 合法。
证明很简单,\(y\le2x\iff y-x\le x\),因为 \(y-x\le a\),故成立。有了这个结论,我们可以做很多事。
我们可以证明,将初始元素升序排序后,合法合并一定是一段段的。如下(图片来自 \(\texttt{lzqy_}\))
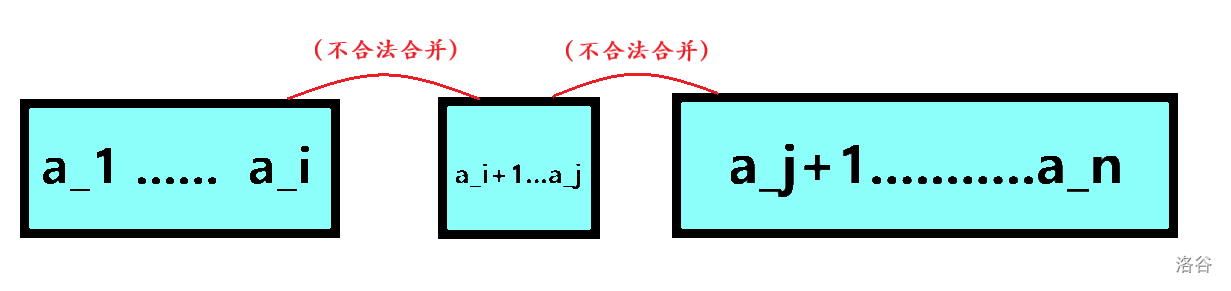
且所有不合法合并一定是形如 \(2\sum\limits_{i=1}^{x-1}a_i<a_{x}\)。于是我们就将原来动态的合并转化为了静态问题。
按值域分块,\([2^0,2^1),[2^1,2^2)\cdots[2^{29},2^{30})\)。则每块内只有第一个元素可能非法。逐块判断即可。复杂度 \(O(n\log x)\)。
标签:le,题解,合并,每次,合法,CF1098D,危险 From: https://www.cnblogs.com/FishJokes/p/17080767.html