import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
data = pd.read_csv('./mnist_train.csv')
print('Data: ', data)
print('Datatype: ', type(data))
print('Data_array: ', np.array(data))
print('Data_array_type: ', type(np.array(data)))
print('Data shape: ', data.shape)
# 首次通过 pandas.read_csv() 读入的数据为 pandas_Dataframe 实例
# 需要通过 np.array() 转换为 np.ndarray 类型
data = np.array(data)
Data: label 1x1 1x2 1x3 1x4 1x5 1x6 1x7 1x8 1x9 ... 28x19 28x20 \
0 5 0 0 0 0 0 0 0 0 0 ... 0 0
1 0 0 0 0 0 0 0 0 0 0 ... 0 0
2 4 0 0 0 0 0 0 0 0 0 ... 0 0
3 1 0 0 0 0 0 0 0 0 0 ... 0 0
4 9 0 0 0 0 0 0 0 0 0 ... 0 0
... ... ... ... ... ... ... ... ... ... ... ... ... ...
59995 8 0 0 0 0 0 0 0 0 0 ... 0 0
59996 3 0 0 0 0 0 0 0 0 0 ... 0 0
59997 5 0 0 0 0 0 0 0 0 0 ... 0 0
59998 6 0 0 0 0 0 0 0 0 0 ... 0 0
59999 8 0 0 0 0 0 0 0 0 0 ... 0 0
28x21 28x22 28x23 28x24 28x25 28x26 28x27 28x28
0 0 0 0 0 0 0 0 0
1 0 0 0 0 0 0 0 0
2 0 0 0 0 0 0 0 0
3 0 0 0 0 0 0 0 0
4 0 0 0 0 0 0 0 0
... ... ... ... ... ... ... ... ...
59995 0 0 0 0 0 0 0 0
59996 0 0 0 0 0 0 0 0
59997 0 0 0 0 0 0 0 0
59998 0 0 0 0 0 0 0 0
59999 0 0 0 0 0 0 0 0
[60000 rows x 785 columns]
Datatype: <class 'pandas.core.frame.DataFrame'>
Data_array: [[5 0 0 ... 0 0 0]
[0 0 0 ... 0 0 0]
[4 0 0 ... 0 0 0]
...
[5 0 0 ... 0 0 0]
[6 0 0 ... 0 0 0]
[8 0 0 ... 0 0 0]]
Data_array_type: <class 'numpy.ndarray'>
Data shape: (60000, 785)
print('np.shape return type: ', type(data.shape))
# np.ndarray.shape 可以获得一个具有两个元素的 tuple 类型的返回值
m, n = data.shape # m rows, n columns
print('%d rows, %d columns.'%(m,n))
print('Data before shuffle:\n ', data)
# 将训练集随机打乱顺序
np.random.shuffle(data)
print('Data after shuffle:\n ', data)
print('Total training dataset shape: ', data.shape)
np.shape return type: <class 'tuple'>
60000 rows, 785 columns.
Data before shuffle:
[[5 0 0 ... 0 0 0]
[0 0 0 ... 0 0 0]
[4 0 0 ... 0 0 0]
...
[5 0 0 ... 0 0 0]
[6 0 0 ... 0 0 0]
[8 0 0 ... 0 0 0]]
Data after shuffle:
[[0 0 0 ... 0 0 0]
[4 0 0 ... 0 0 0]
[5 0 0 ... 0 0 0]
...
[4 0 0 ... 0 0 0]
[2 0 0 ... 0 0 0]
[3 0 0 ... 0 0 0]]
Total training dataset shape: (60000, 785)
# 取出 dev_dataset 将第一列的标签通过转置放到第一行
data_dev = data[0:1000].T
print('Dev dataset shape: ', data_dev.shape)
# 取出 dev_dataset 的样本和标签
Y_dev = data_dev[0] # 标签
print('Y_dev_data(label): ', Y_dev)
X_dev = data_dev[1:] # 样本
print('X_dev_data(example): ', X_dev)
# 验证样本数据行是否完整,一行就是一张图片的展开
print('Is flatten pic valid: %s'%('True' if len(X_dev[:,int(np.random.randn()*100)]) == 28 * 28 else 'False'))
print((X_dev / 255.)[:,0]) # 像素点色彩强度值归一化优化运算速度
Dev dataset shape: (785, 1000)
Y_dev_data(label): [0 4 5 3 1 8 0 2 5 3 4 4 3 4 3 0 5 2 4 4 5 8 3 0 1 5 0 9 7 4 9 8 3 6 8 2 4
3 6 2 9 8 3 5 3 2 3 3 6 3 2 4 3 4 8 8 5 8 9 4 8 3 3 3 3 7 9 7 4 3 1 8 2 2
4 2 2 6 9 4 0 4 3 3 6 6 6 5 9 9 3 8 7 5 7 1 4 2 0 9 1 7 5 7 2 0 6 2 5 1 8
6 8 3 5 3 7 8 0 2 9 4 7 4 5 1 3 1 1 7 2 7 7 5 9 5 4 0 7 3 6 6 3 0 8 4 8 0
1 2 7 5 4 1 1 5 6 7 1 0 3 9 0 6 8 9 3 2 8 6 1 5 5 8 6 5 1 0 7 1 9 3 1 4 9
3 0 1 9 2 2 3 0 6 1 5 5 0 1 4 7 5 2 7 1 3 7 7 8 3 7 5 4 4 5 1 6 3 2 2 0 3
4 7 9 3 1 9 0 8 7 9 3 2 0 1 9 5 0 2 2 2 2 0 9 3 2 8 1 0 5 4 7 4 8 6 4 5 4
5 5 7 9 3 5 3 7 8 7 9 4 7 1 2 5 1 3 9 5 4 2 8 7 3 7 6 2 8 2 3 3 8 4 1 3 8
2 4 5 6 8 8 8 0 8 5 9 9 2 2 3 3 3 0 4 9 4 0 5 9 0 1 1 0 9 1 5 9 6 0 4 8 7
4 0 0 3 4 8 6 7 6 9 7 2 5 5 4 7 9 4 5 4 6 1 4 4 6 1 2 3 5 3 8 9 5 6 7 7 0
6 9 7 4 2 6 4 7 0 0 3 4 3 1 4 1 4 3 9 1 1 8 0 9 4 2 1 9 5 3 4 7 0 9 1 5 3
7 7 8 3 5 5 0 8 3 8 3 7 7 4 3 6 5 9 9 5 4 4 0 6 1 2 5 8 8 5 7 3 3 5 3 3 4
8 8 5 6 9 8 4 3 4 9 1 7 9 0 7 6 7 8 0 8 7 7 7 2 9 9 1 7 0 8 1 4 8 6 5 4 8
4 1 5 3 4 9 0 6 4 8 1 1 9 1 5 4 8 5 9 1 1 9 6 2 8 7 2 8 5 9 0 4 9 8 1 2 8
8 6 6 0 9 4 6 4 3 1 6 7 3 7 5 0 4 8 1 1 4 1 9 4 4 2 4 9 3 8 4 1 9 4 4 4 2
1 0 5 0 8 4 6 1 7 4 2 0 4 4 5 9 8 7 4 5 4 8 7 8 4 1 4 8 5 6 8 1 7 8 5 6 3
4 6 7 2 6 5 6 4 7 6 7 9 3 1 1 4 7 3 7 1 8 3 3 3 4 7 0 1 5 7 9 9 7 8 1 6 6
0 4 6 3 8 2 1 9 7 7 9 7 9 5 7 7 5 9 2 6 6 0 9 2 4 1 6 0 1 0 9 2 6 5 8 2 9
2 2 6 1 4 9 7 2 1 4 2 7 1 5 3 5 2 2 8 3 5 1 6 3 3 0 7 5 3 0 3 0 6 7 8 9 3
0 3 2 3 5 8 7 2 2 2 1 5 6 4 0 0 2 3 5 1 4 1 8 4 9 0 1 0 1 1 1 7 6 1 7 7 5
4 8 3 5 9 7 6 2 8 4 7 2 8 0 8 0 8 8 1 2 8 6 1 0 0 7 4 4 6 0 5 2 0 3 3 7 0
8 9 7 1 9 6 4 9 8 7 6 1 6 7 6 9 7 7 3 5 1 6 9 8 1 7 3 2 1 0 7 9 3 7 5 9 4
9 4 8 3 1 5 2 7 9 5 2 1 5 0 2 1 8 5 1 1 1 3 0 0 9 9 2 5 5 6 8 5 7 1 8 1 9
4 1 0 1 7 9 1 3 5 8 9 7 8 8 3 4 6 5 1 5 1 8 0 3 0 4 1 0 5 9 5 0 4 9 6 6 0
3 7 5 0 8 4 1 1 2 6 0 9 6 3 0 5 8 2 3 5 1 1 5 1 8 9 3 1 6 8 8 3 9 5 7 3 4
6 6 2 5 8 3 3 3 6 5 0 7 7 7 5 7 3 3 1 0 9 1 7 0 1 8 2 7 6 0 9 9 3 6 8 3 8
2 6 4 0 9 9 0 8 1 2 4 0 7 3 0 3 7 5 1 7 3 8 3 1 4 5 4 6 6 1 4 0 7 4 1 6 7
8]
X_dev_data(example): [[0 0 0 ... 0 0 0]
[0 0 0 ... 0 0 0]
[0 0 0 ... 0 0 0]
...
[0 0 0 ... 0 0 0]
[0 0 0 ... 0 0 0]
[0 0 0 ... 0 0 0]]
Is flatten pic valid: True
[0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0.65882353 0.99607843 0.99607843 1. 0.99607843
0.99607843 0.68627451 0.29019608 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0.45490196 0.61960784 0.8627451
0.99215686 0.99215686 0.99215686 0.99215686 0.99215686 0.99215686
0.96470588 0.38431373 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.74117647
0.92941176 0.97254902 0.99215686 0.99215686 0.99215686 0.84705882
0.74901961 0.8745098 0.99215686 0.99215686 0.99215686 0.61176471
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0.48235294 0.54901961 0.90196078 0.99215686 0.99215686
0.8 0.80392157 0.83921569 0.18431373 0. 0.51372549
0.99215686 0.99215686 0.99215686 0.61176471 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0.09803922 0.88235294
0.99215686 0.99215686 0.99215686 0.84313725 0.08627451 0.09019608
0.09803922 0. 0. 0.07058824 0.25098039 0.99215686
0.99215686 0.94117647 0.26666667 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0.11764706 0.76470588 0.99215686 0.99215686 0.99215686
0.78823529 0.14117647 0. 0. 0. 0.
0. 0. 0.14117647 0.99215686 0.99215686 0.99215686
0.30588235 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.31372549
0.99215686 0.99215686 0.99215686 0.83529412 0.11764706 0.
0. 0. 0. 0. 0. 0.
0.14117647 0.99215686 0.99215686 0.95294118 0.2745098 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0.92941176 0.99215686 0.99215686
0.99215686 0.20392157 0. 0. 0. 0.
0. 0. 0. 0. 0.42745098 0.99215686
0.99215686 0.61176471 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0.45490196 0.97254902 0.99215686 0.99215686 0.97254902 0.19607843
0. 0. 0. 0. 0. 0.
0. 0.01960784 0.83137255 0.99215686 0.99215686 0.61176471
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0.61960784 0.99215686
0.99215686 0.99215686 0.50980392 0. 0. 0.
0. 0. 0. 0. 0. 0.51372549
0.99215686 0.99215686 0.99215686 0.61176471 0. 0.
0. 0. 0. 0. 0. 0.
0. 0.20784314 0.8627451 0.99215686 0.99215686 0.87843137
0.17647059 0. 0. 0. 0. 0.
0. 0. 0. 0.51372549 0.99215686 0.99215686
0.99215686 0.61176471 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.31372549
0.99215686 0.99215686 0.99215686 0.62745098 0. 0.
0. 0. 0. 0. 0. 0.
0.39607843 0.97647059 0.99215686 0.99215686 0.97254902 0.44705882
0. 0. 0. 0. 0. 0.
0. 0. 0. 0.31372549 0.99215686 0.99215686
0.99215686 0.5372549 0. 0. 0. 0.
0. 0. 0. 0.34901961 0.95294118 0.99215686
0.99215686 0.99215686 0.51372549 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0.31372549 0.99215686 0.99215686 0.99215686 0.81960784
0. 0. 0. 0. 0. 0.
0.20392157 0.67058824 0.99215686 0.99215686 0.99215686 0.58823529
0.02352941 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.14901961
0.79607843 0.99215686 0.99215686 0.90980392 0.26666667 0.
0. 0. 0. 0.34509804 0.97647059 0.99215686
0.99215686 0.99215686 0.91764706 0.2627451 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0.53333333 0.98431373
0.99215686 0.99215686 0.90980392 0.27843137 0.14117647 0.14117647
0.38039216 0.93333333 0.99215686 0.99215686 0.99215686 0.91764706
0.25882353 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0.92941176 0.99215686 0.99215686
0.99215686 0.99215686 0.99215686 0.99215686 0.99215686 0.99215686
0.99215686 0.99215686 0.99215686 0.47843137 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0.88235294 0.99215686 0.99215686 0.99215686 0.99215686
0.99215686 0.99215686 0.99215686 0.99215686 0.99215686 0.94901961
0.78039216 0.11372549 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.15294118
0.61176471 0.94117647 0.99215686 0.99215686 0.99215686 0.99215686
0.99215686 0.99215686 0.88627451 0.25490196 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.26666667
0.30588235 0.37647059 0.99215686 0.99215686 0.99215686 0.5372549
0.21960784 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. ]
data_train = data[1000:m].T # 后 59000 个样本作为训练集
Y_train = data_train[0]
X_train = data_train[1:]
print('Data validation: %s'%('True' if len(X_train[:, int(np.random.rand()*1000)]) == 28 * 28 else 'False'))
# 色值归一化
X_train = X_train / 255.
# 训练集大小
_, m_train = X_train.shape
print('X_train_col: ', m_train) # (x1, x2, ... , x58999, x59000)
Y_train
Data validation: True
X_train_col: 59000
array([1, 3, 2, ..., 4, 2, 3], dtype=int64)
# 可以发现 np.random.rand() 范围是 (0, 1), np.random.randn()
# for _ in range(10):
# print(np.random.rand(1,2), np.random.randn(1,2))
# 生成一个 randn() 矩阵
# test_randn_arr = np.array([np.random.randn() for _ in range(5000)]) # np.random.randn((5000)) 相同效果
# test_randn_arr
# 当数量足够大时,np.random.randn() 生成的数字其均值趋近0,可知 np.random.randn() 生成正态分布
# print(np.mean(test_randn_arr))
# np.max() & np.maximum()
# np.max() 求序列的最值,最少接受一个参数
# np.maximum() 两个序列逐位比较,最少接受两个参数,返回每一位比较后的最大值组成的序列
# test_arr = np.random.rand(3,3)-0.5
# 如果是 0 矩阵,相当于 broadcast 为 0 矩阵,常数则是 n 倍全 1 矩阵
# print(np.maximum(test_arr, 2)) # 返回 3*3 的 2 倍 全 1 矩阵
# 生成初始权重偏置(随机值)
def init_params():
# 减去 0.5 使 W1 的区间在 (-0.5, 0.5)
W1 = np.random.rand(30, 28*28) - 0.5
b1 = np.random.rand(30, 1) - 0.5
W2 = np.random.rand(10, 30) - 0.5
b2 = np.random.rand(10, 1) - 0.5
return W1, b1, W2, b2
# ReLU进行激活
def ReLU(Z):
return np.maximum(Z, 0)
# ReLU导数
def deriv_ReLU(Z):
return Z > 0
# 将输出结果归一化(概率化)
# 出现数值溢出,弃用
# def softmax(Z):
# return np.exp(Z) / sum(np.exp(Z))
# 优化softmax函数避免溢出
def softmax(x):
max = np.max(x)
return np.exp(x-max)/sum(np.exp(x-max))
# Z = np.array([
# [1,2,3],
# [4,5,6],
# [7,8,9]
# ])
# 前向传播
def forward_propagation(W1, b1, W2, b2, X):
Z1 = np.dot(W1, X) + b1
A1 = ReLU(Z1)
Z2 = np.dot(W2, A1) + b2
A2 = softmax(Z2)
return Z1, A1, Z2, A2
# 标签 one-hot 编码
def one_hot(Y):
one_hot_Y = np.zeros((Y.size, Y.max() + 1))
one_hot_Y[np.arange(Y.size), Y] = 1
one_hot_Y = one_hot_Y.T
return one_hot_Y
# 反向传播
def backward_propagation(Z1, A1, Z2, A2, W1, W2, X, Y):
one_hot_Y = one_hot(Y)
dZ2 = A2 - one_hot_Y
dW2 = 1 / m * dZ2.dot(A1.T)
db2 = 1 / m * np.sum(dZ2)
dZ1 = W2.T.dot(dZ2) * deriv_ReLU(Z1)
dW1 = 1 / m * dZ1.dot(X.T)
db1 = 1 / m * np.sum(dZ1)
return dW1, db1, dW2, db2
# 使用反向传播得到的ΔW和Δb进行原参数的调整(梯度下降法)
def update_params(W1, b1, W2, b2, dW1, db1, dW2, db2, alpha):
W1 = W1 - alpha * dW1
b1 = b1 - alpha * db1
W2 = W2 - alpha * dW2
b2 = b2 - alpha * db2
return W1, b1, W2, b2
# 从10*m输出中找到softmax值最大者
def get_predictions(A2):
return np.argmax(A2, 0)
# 返回预测正确者在测试集(Y_dev)中的占比,作为准确度
def get_accuracy(predictions, Y):
print(predictions, Y)
return np.sum(predictions == Y) / Y.size
# 进行iterations次的迭代,完成梯度下降法对参数的调整
def gradient_descent(X, Y, alpha, iterations):
W1, b1, W2, b2 = init_params()
for i in range(iterations):
Z1, A1, Z2, A2 = forward_propagation(W1, b1, W2, b2, X)
dW1, db1, dW2, db2 = backward_propagation(Z1, A1, Z2, A2, W1, W2, X, Y)
W1, b1, W2, b2 = update_params(W1, b1, W2, b2, dW1, db1, dW2, db2, alpha)
if i % 10 == 0:
print("Iteration: ", i)
predictions = get_predictions(A2)
print(get_accuracy(predictions, Y))
return W1, b1, W2, b2
W1, b1, W2, b2 = gradient_descent(X_train, Y_train, 0.10, 500)
Iteration: 0
[9 6 9 ... 7 7 9] [1 3 2 ... 4 2 3]
0.08171186440677966
Iteration: 10
[3 6 6 ... 2 7 5] [1 3 2 ... 4 2 3]
0.22979661016949152
Iteration: 20
[5 9 6 ... 2 7 5] [1 3 2 ... 4 2 3]
0.35710169491525423
Iteration: 30
[5 9 6 ... 2 7 5] [1 3 2 ... 4 2 3]
0.4587457627118644
Iteration: 40
[5 9 6 ... 2 4 3] [1 3 2 ... 4 2 3]
0.5425254237288135
Iteration: 50
[5 8 6 ... 2 4 3] [1 3 2 ... 4 2 3]
0.6005932203389831
Iteration: 60
[5 8 6 ... 2 4 3] [1 3 2 ... 4 2 3]
0.6429322033898305
Iteration: 70
[5 8 6 ... 4 4 3] [1 3 2 ... 4 2 3]
0.673864406779661
Iteration: 80
[5 8 6 ... 4 4 3] [1 3 2 ... 4 2 3]
0.6992372881355933
Iteration: 90
[5 5 6 ... 4 2 3] [1 3 2 ... 4 2 3]
0.717728813559322
Iteration: 100
[5 5 6 ... 4 2 3] [1 3 2 ... 4 2 3]
0.7345423728813559
Iteration: 110
[5 5 6 ... 4 2 3] [1 3 2 ... 4 2 3]
0.7476440677966102
Iteration: 120
[5 5 6 ... 4 2 3] [1 3 2 ... 4 2 3]
0.7585762711864407
Iteration: 130
[5 5 6 ... 4 2 3] [1 3 2 ... 4 2 3]
0.7692033898305085
Iteration: 140
[5 5 6 ... 4 2 3] [1 3 2 ... 4 2 3]
0.778
Iteration: 150
[5 5 6 ... 4 2 3] [1 3 2 ... 4 2 3]
0.7866271186440678
Iteration: 160
[5 5 6 ... 4 2 3] [1 3 2 ... 4 2 3]
0.7936101694915254
Iteration: 170
[5 5 6 ... 4 2 3] [1 3 2 ... 4 2 3]
0.8004745762711865
Iteration: 180
[5 5 6 ... 4 2 3] [1 3 2 ... 4 2 3]
0.8065593220338984
Iteration: 190
[5 5 6 ... 4 2 3] [1 3 2 ... 4 2 3]
0.8118983050847458
Iteration: 200
[5 5 6 ... 4 2 3] [1 3 2 ... 4 2 3]
0.8164915254237288
Iteration: 210
[5 3 6 ... 4 2 3] [1 3 2 ... 4 2 3]
0.8213898305084746
Iteration: 220
[5 3 6 ... 4 2 3] [1 3 2 ... 4 2 3]
0.8257457627118644
Iteration: 230
[5 3 6 ... 4 2 3] [1 3 2 ... 4 2 3]
0.8292372881355933
Iteration: 240
[5 3 6 ... 4 2 3] [1 3 2 ... 4 2 3]
0.8325762711864407
Iteration: 250
[5 3 6 ... 4 2 3] [1 3 2 ... 4 2 3]
0.8360677966101695
Iteration: 260
[5 3 6 ... 4 2 3] [1 3 2 ... 4 2 3]
0.8393220338983051
Iteration: 270
[5 3 6 ... 4 2 3] [1 3 2 ... 4 2 3]
0.8421525423728814
Iteration: 280
[5 3 6 ... 4 2 3] [1 3 2 ... 4 2 3]
0.8444745762711865
Iteration: 290
[5 3 6 ... 4 2 3] [1 3 2 ... 4 2 3]
0.8469491525423729
Iteration: 300
[3 3 6 ... 4 2 3] [1 3 2 ... 4 2 3]
0.8492542372881355
Iteration: 310
[3 3 6 ... 4 2 3] [1 3 2 ... 4 2 3]
0.8509152542372881
Iteration: 320
[3 3 6 ... 4 2 3] [1 3 2 ... 4 2 3]
0.8524406779661017
Iteration: 330
[3 3 6 ... 4 2 3] [1 3 2 ... 4 2 3]
0.8550169491525423
Iteration: 340
[3 3 6 ... 4 2 3] [1 3 2 ... 4 2 3]
0.8570677966101695
Iteration: 350
[3 3 6 ... 4 2 3] [1 3 2 ... 4 2 3]
0.8587288135593221
Iteration: 360
[3 3 6 ... 4 2 3] [1 3 2 ... 4 2 3]
0.8604237288135593
Iteration: 370
[3 3 6 ... 4 2 3] [1 3 2 ... 4 2 3]
0.8619661016949153
Iteration: 380
[3 3 6 ... 4 2 3] [1 3 2 ... 4 2 3]
0.8637457627118644
Iteration: 390
[3 3 6 ... 4 2 3] [1 3 2 ... 4 2 3]
0.8653220338983051
Iteration: 400
[3 3 6 ... 4 2 3] [1 3 2 ... 4 2 3]
0.8664237288135593
Iteration: 410
[3 3 6 ... 4 2 3] [1 3 2 ... 4 2 3]
0.867457627118644
Iteration: 420
[3 3 6 ... 4 2 3] [1 3 2 ... 4 2 3]
0.8688474576271187
Iteration: 430
[3 3 6 ... 4 2 3] [1 3 2 ... 4 2 3]
0.8702203389830508
Iteration: 440
[3 3 6 ... 4 2 3] [1 3 2 ... 4 2 3]
0.8714745762711864
Iteration: 450
[3 3 6 ... 4 2 3] [1 3 2 ... 4 2 3]
0.873135593220339
Iteration: 460
[3 3 2 ... 4 2 3] [1 3 2 ... 4 2 3]
0.8742881355932204
Iteration: 470
[3 3 2 ... 4 2 3] [1 3 2 ... 4 2 3]
0.8754406779661017
Iteration: 480
[3 3 2 ... 4 2 3] [1 3 2 ... 4 2 3]
0.8764406779661017
Iteration: 490
[3 3 2 ... 4 2 3] [1 3 2 ... 4 2 3]
0.8772542372881356
~87.7% accuracy on training set.
# 进行一次前向传播得到预测值
def make_predictions(X, W1, b1, W2, b2):
_, _, _, A2 = forward_propagation(W1, b1, W2, b2, X)
predictions = get_predictions(A2)
return predictions
# 以当前的权重和偏置值作为参数进行一次预测
def test_prediction(index, W1, b1, W2, b2):
current_image = X_train[:, index, None]
prediction = make_predictions(X_train[:, index, None], W1, b1, W2, b2)
label = Y_train[index]
print("Prediction: ", prediction)
print("Label: ", label)
current_image = current_image.reshape((28, 28)) * 255
plt.gray()
plt.imshow(current_image, interpolation='nearest')
plt.show()
test_prediction(0, W1, b1, W2, b2)
test_prediction(1, W1, b1, W2, b2)
test_prediction(2, W1, b1, W2, b2)
test_prediction(3, W1, b1, W2, b2)
Prediction: [3]
Label: 1
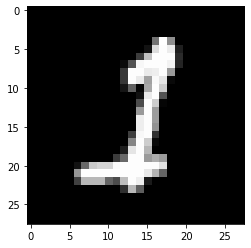
Prediction: [3]
Label: 3
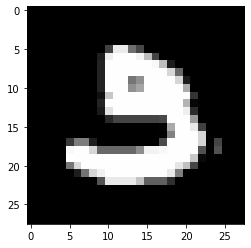
Prediction: [2]
Label: 2
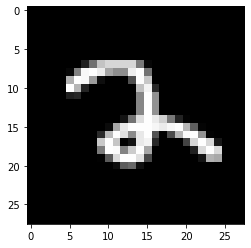
Prediction: [6]
Label: 6
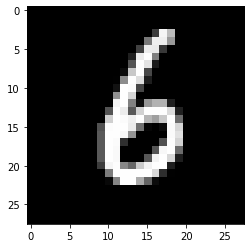
import cv2 as cv
current_image = cv.imread('./8.png')
gray_image = cv.cvtColor(current_image, cv.COLOR_BGR2GRAY)
plt.imshow(gray_image)
plt.show()
gray_image = gray_image.reshape(784, 1)
gray_image.reshape(784, 1) / 255
# print(gray_image.shape)
def test_user_prediction(gray_image, W1, b1, W2, b2):
prediction = make_predictions(gray_image, W1, b1, W2, b2)
print("Prediction: ", prediction)
# current_image = X_train[:, 1, None]
# current_image.shape
test_user_prediction(gray_image, W1, b1, W2, b2)
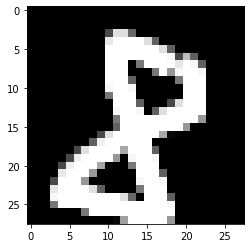
Prediction: [8]
current_image = X_train[:, 12, None]
current_image.shape
(784, 1)