简介

KMP 这个名字的由来：它是三个人：D.E · Knuth 、J.H · Morris 和 V.R · Pratt 同时发现的。

KMP 是一种字符串单模匹配算法，复杂度 \(\operatorname{O(n+k)}\) 。
其中， \(n\) 是主串的长度， \(k\) 是模式串的长度。由于至少要遍历主串和模式串的每个字符，此类算法的最佳复杂度是 \(\operatorname{O(n+k)}\) ，KMP 差不多达到了此类算法能达到的最佳时间复杂度。

实现

模板题（AcWing.831）

题目描述

给定一个字符串 \(s\)，以及一个模式串 \(p\)，所有字符串中只包含大小写英文字母以及阿拉伯数字。求出模式串 \(p\) 在字符串 \(s\) 中所有出现的位置的起始下标。

• 模式串 \(p\) 在字符串 \(s\) 中多次作为子串出现。

样例

in：

3
aba
5
ababa

out：

0 2

KMP 实现

思路

首先想想暴力。
用 \(flag\) 表示是否匹配。先设 \(flag=1\) ， 再用 \(i\) 枚举起始位置， \(j\) 枚举模式串的每个字符下标，如果有不匹配的，则 \(flag=0\) 。

for(ll i=1;i<=n;i++)
{
    bool flag=1;
    for(ll j=1;j<=m;j++)
        if(s[i]!=p[j]){flag=0;break;}
}

接下来要把它优化。

暴力匹配算法在每个字符失配后都回溯到了 \(i\) 的位置，显然这会浪费很多时间。
如果我们找到模式串 \(p\) 中两个相同的字串，每次匹配就可以从前一个子串
这样一来就可以做到只回溯 \(j\) 。（这里读者自己画图理解，这里很关键）

下图演绎了 KMP 如何匹配主串和模式串（原创的图）。

动态演示：

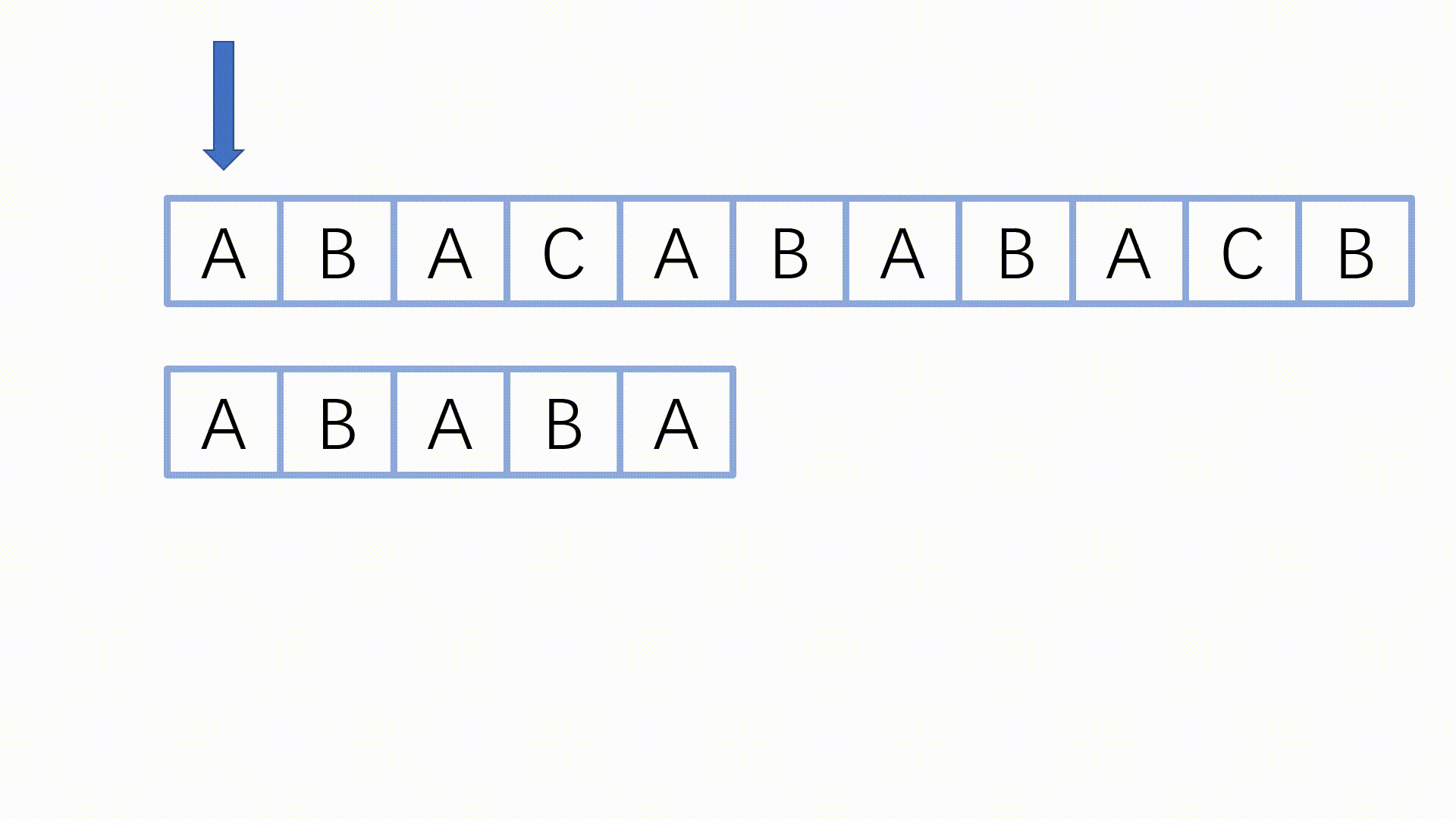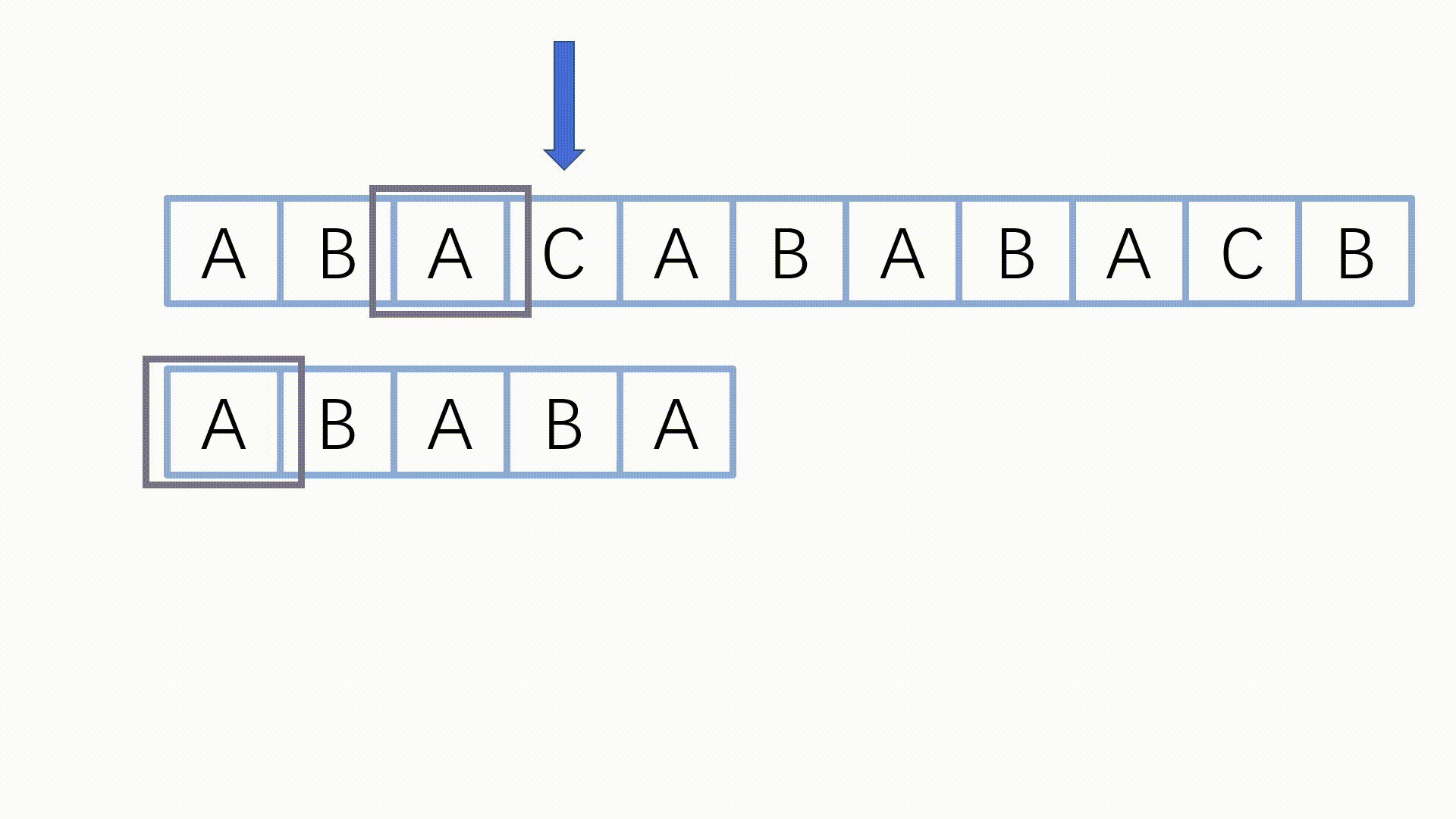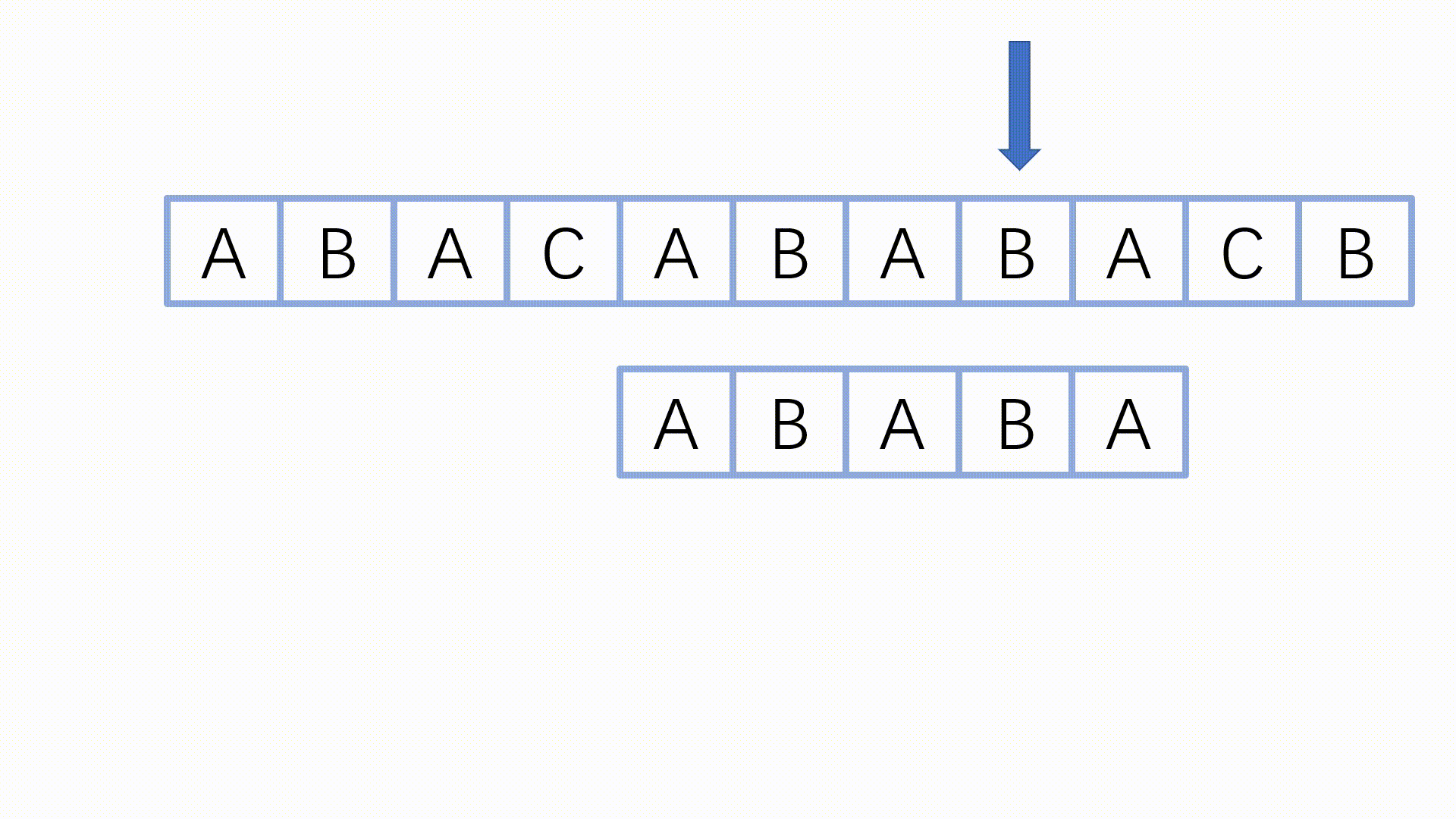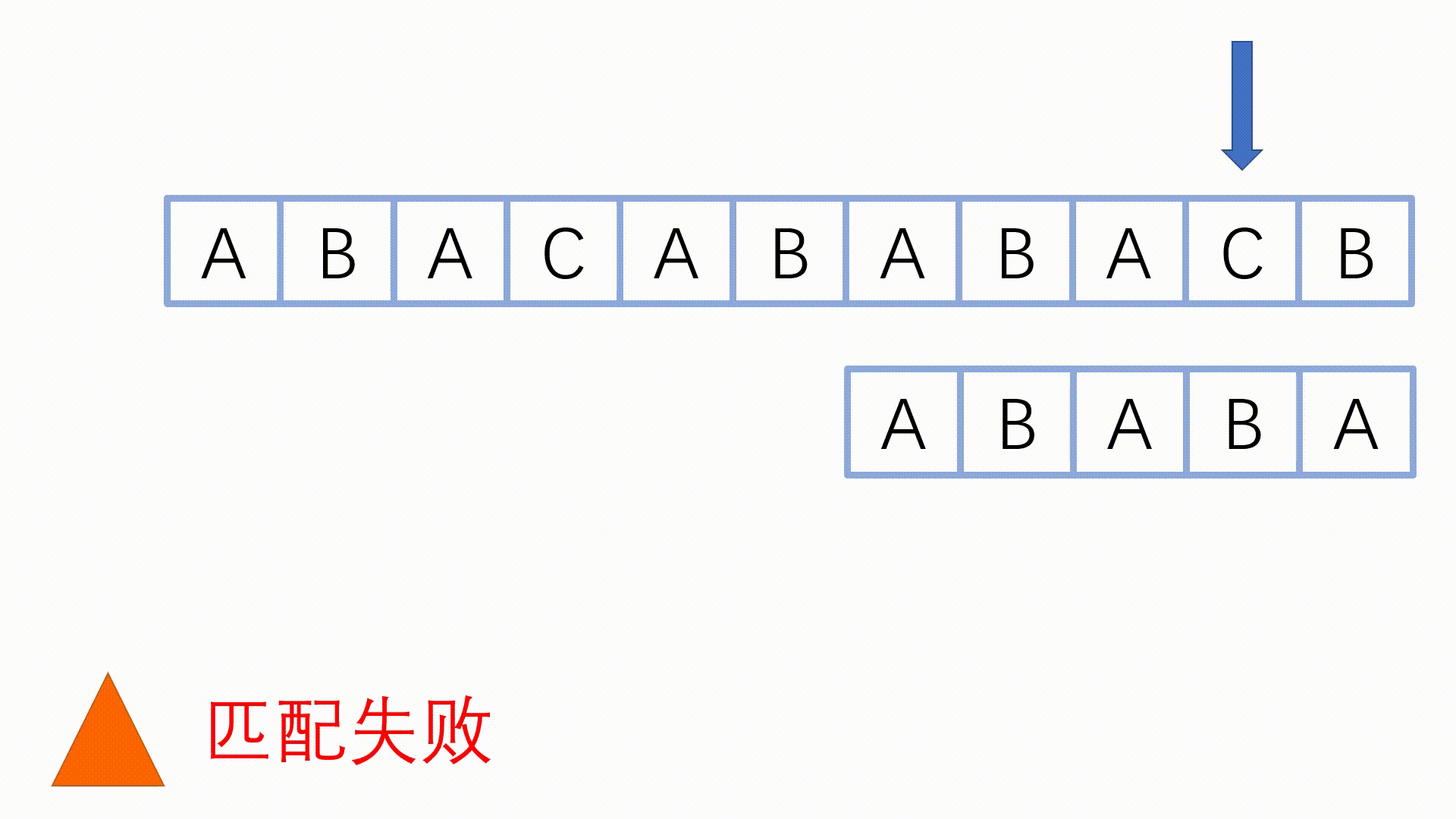
注：如果用 #include <bits/stdc++.h> ，那就不能用 next 做数组名，我在这里用的是 nxt 。

匹配代码

for(ll i=1,j=0;i<=m;i++)
{
    while(j&&s[i]!=p[j+1]) j=nxt[j];
    if(s[i]==p[j+1]) j++;
    if(j==n){write(i-n),putchar(' '),j=nxt[j];}
}

那怎么知道 \(j\) 回溯到哪去呢？
可以预处理出一个 \(next\) 数组，用来维护每个 \(j\) 回溯的位置。

下图演绎了如何预处理出 \(next\) 数组。

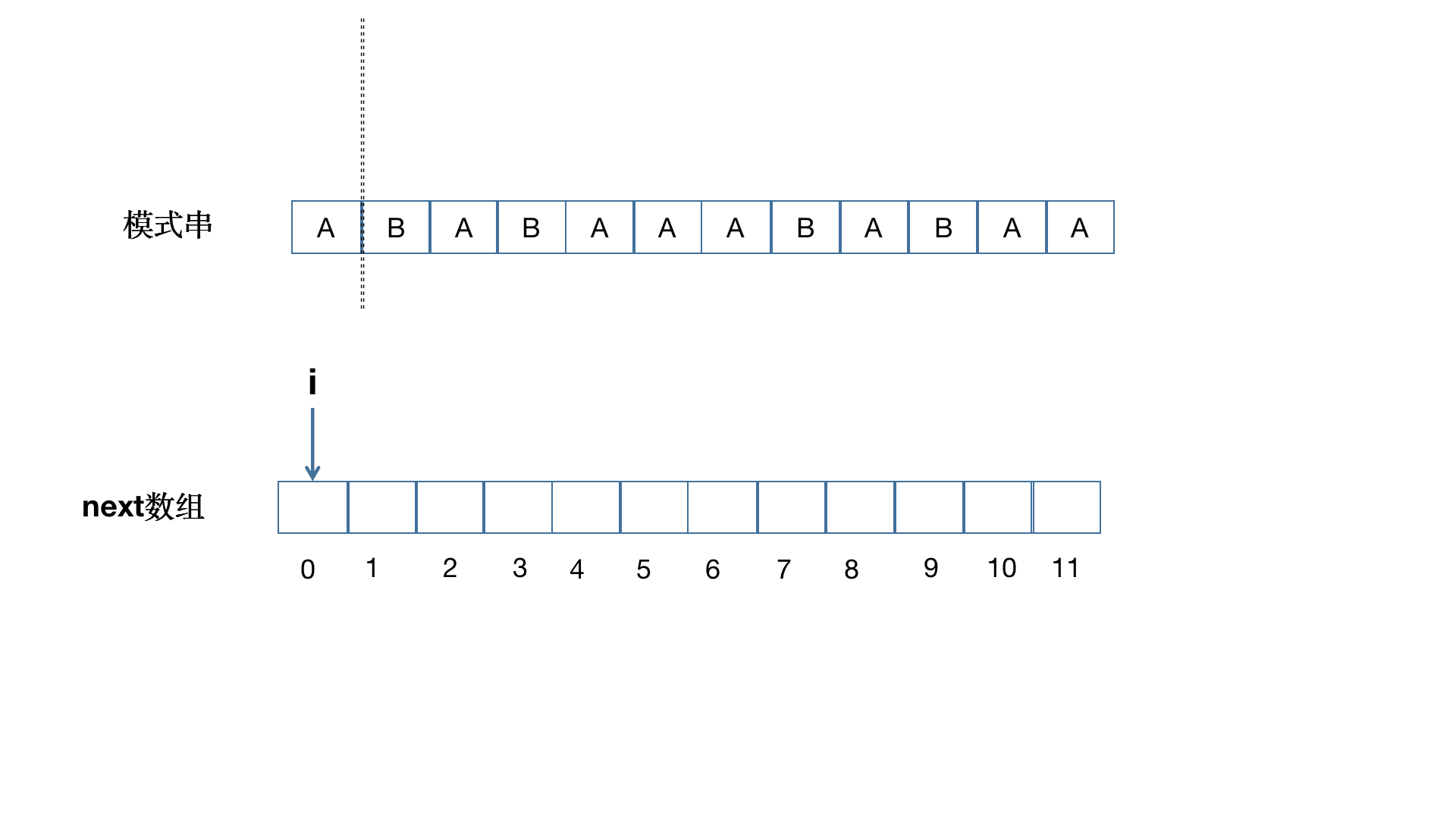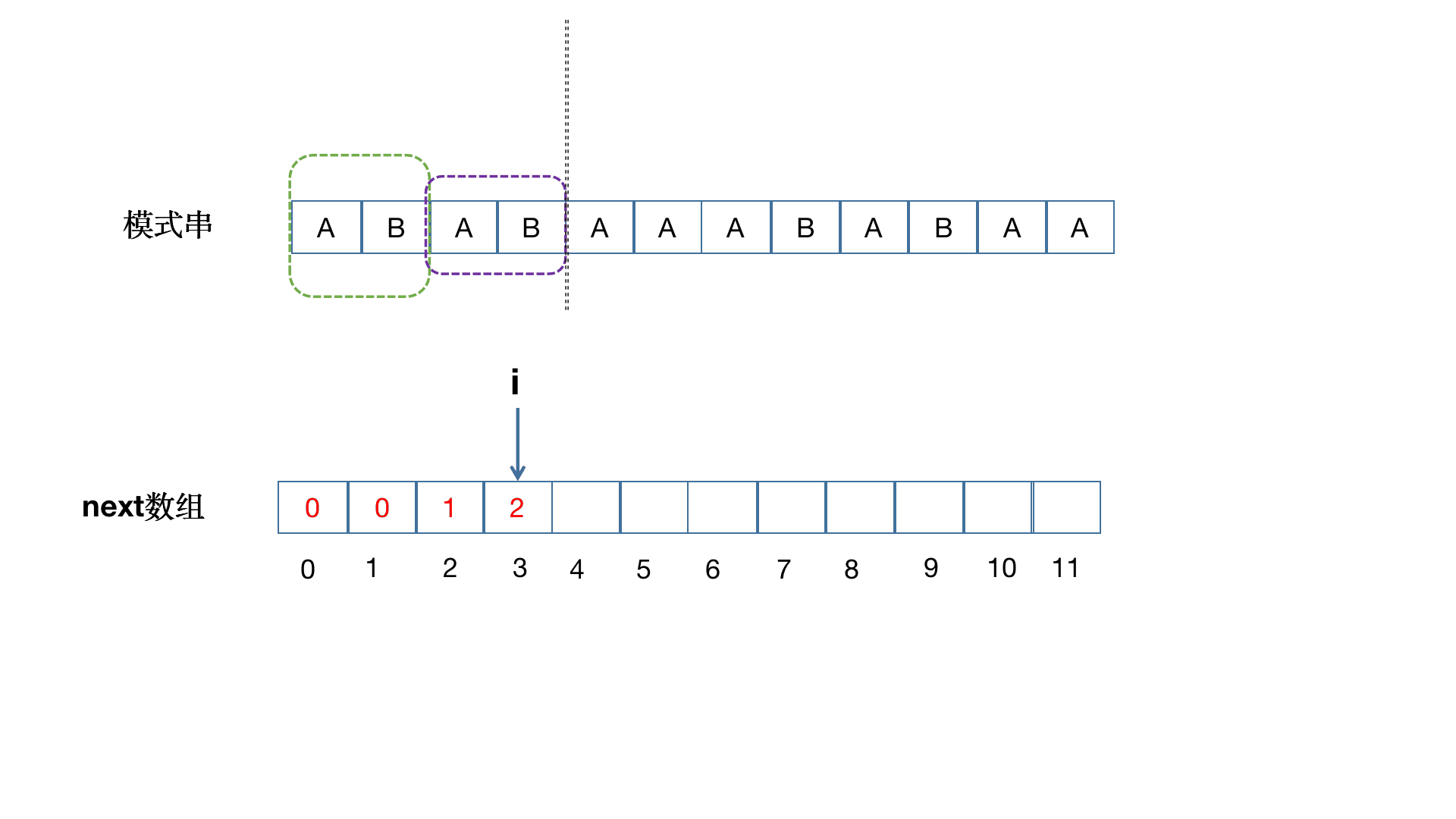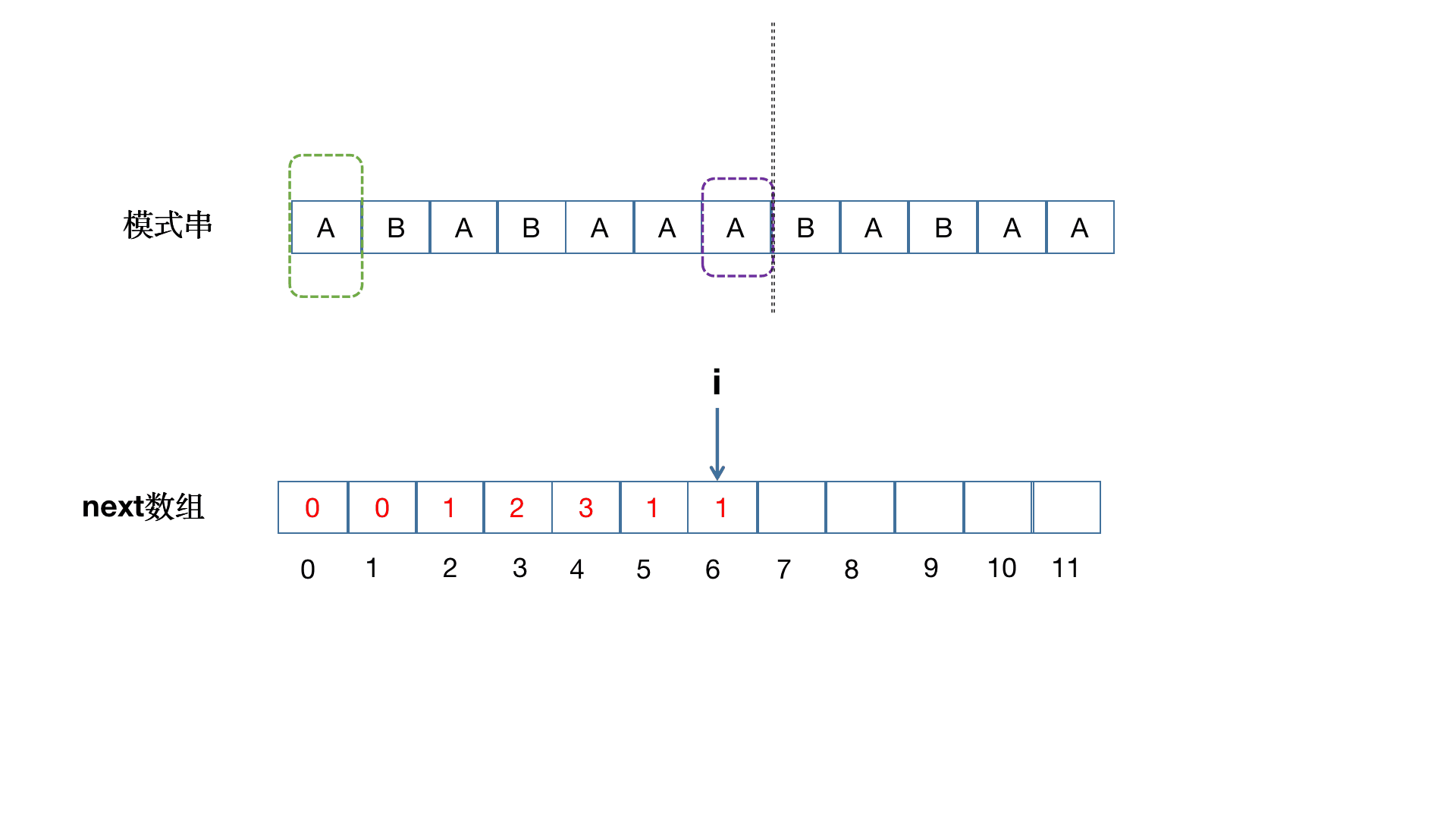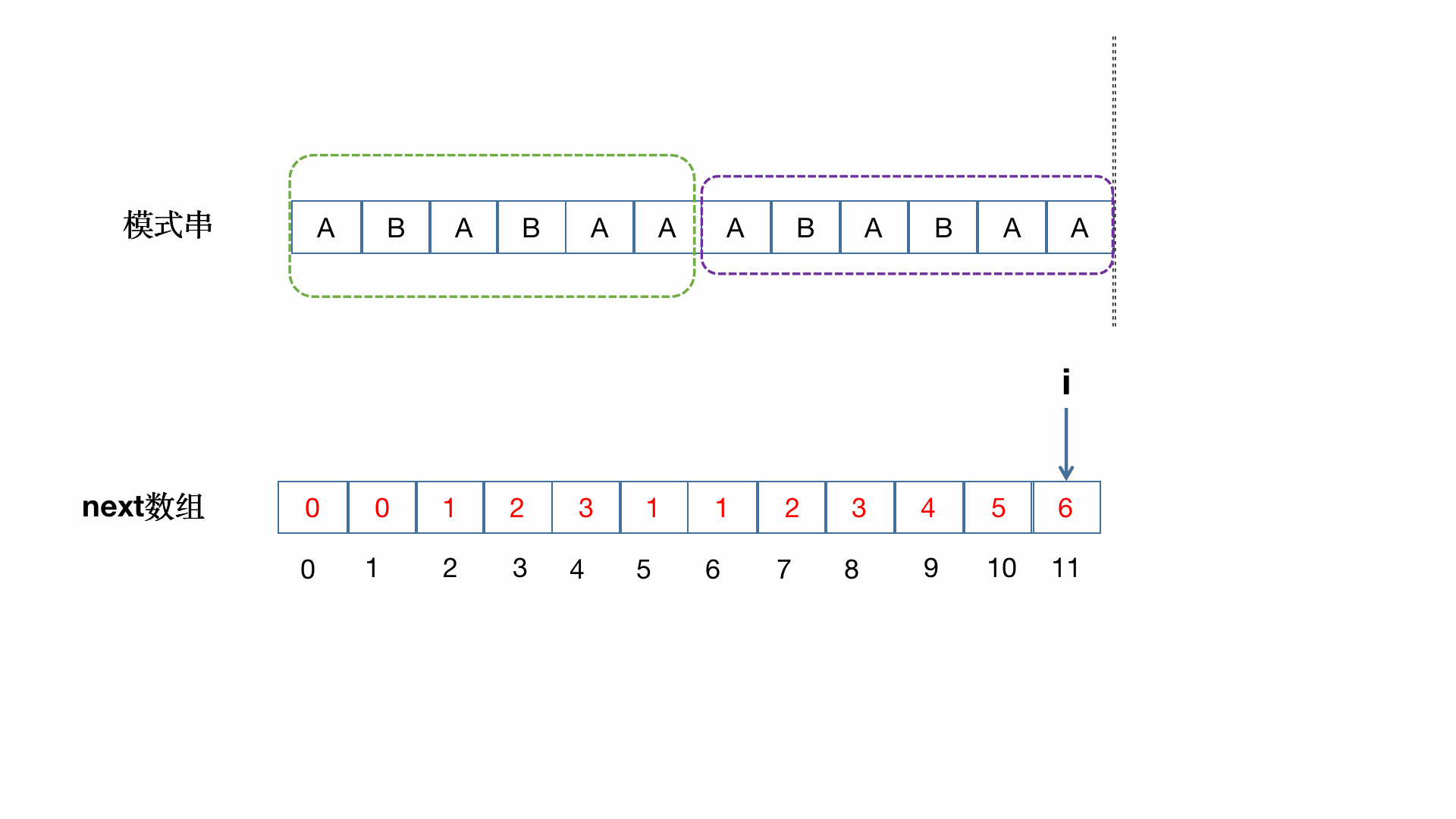
预处理代码

inline void init()
{
    for(ll i=2,j=0;i<=n;i++)
    {
        while(j&&p[i]!=p[j+1]) j=nxt[j];
        if(p[i]==p[j+1]) j++;
        nxt[i]=j;
    }
}

代码

#include <bits/stdc++.h>
#define ll long long
#define rll register ll
#define cll const ll
#define N 1000005
using namespace std;
inline ll read()
{
    rll x=0;bool f=1;static char c=getchar();
    while(!isdigit(c)){if(c=='-') f=0;c=getchar();}
    while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
    return (f==1)?x:-x;
}
inline void write(ll x)
{
    if(x<0) putchar('-'),x=-x;
    if(x>9) write(x/10);
    putchar(x%10+48);
}//卡常
ll n=read(),m,nxt[N];
char p[N],s[N];
inline void init()
{
    for(rll i=2,j=0;i<=n;i++)
    {
        while(j&&p[i]!=p[j+1]) j=nxt[j];
        if(p[i]==p[j+1]) j++;
        nxt[i]=j;
    }
}//初始化next数组
int main()
{
    scanf("%s",p+1);m=read();scanf("%s",s+1);
    init();
    for(rll i=1,j=0;i<=m;i++)
    {
        while(j&&s[i]!=p[j+1]) j=nxt[j];
        if(s[i]==p[j+1]) j++;
        if(j==n){write(i-n),putchar(' '),j=nxt[j];}
    }
    return 0;
}