长脖子鹿放置
题目背景
众周所知,在西洋棋中,我们有城堡、骑士、皇后、主教和长脖子鹿。
题目描述
如图所示,西洋棋的“长脖子鹿”,类似于中国象棋的马,但按照“目”字攻击,且没有中国象棋“别马腿”的规则。(因为长脖子鹿没有马腿)
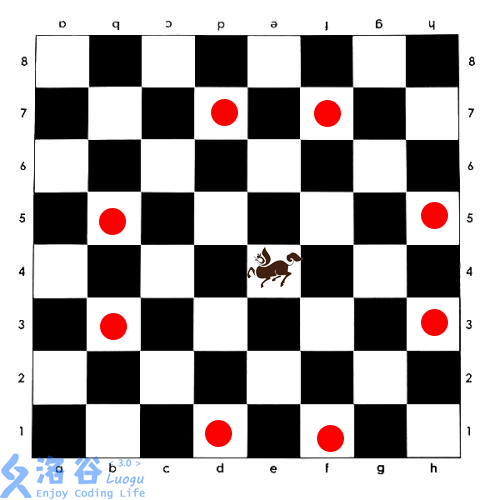
给定一个\(N * M\),的棋盘,有一些格子禁止放棋子。问棋盘上最多能放多少个不能互相攻击的长脖子鹿。
输入格式
输入的第一行为两个正整数\(N\),\(M\),\(K\)。其中\(K\)表示禁止放置长脖子鹿的格子数。
第\(2\)~第\(K+1\)行每一行为两个整数\(X_i, Y_i\),表示禁止放置的格子。
不保证禁止放置的格子互不相同。
输出格式
一行一个正整数,表示最多能放置的长脖子鹿个数。
样例 #1
样例输入 #1
2 2 1
1 1
样例输出 #1
3
样例 #2
样例输入 #2
/*额外提供一组数据*/
8 7 5
1 1
5 4
2 3
4 7
8 3
样例输出 #2
28
提示
重要提示:请务必思考对图的遍历顺序对运行速度的影响
对于\(10\)%的数据, \(1 ≤ N,M ≤ 5\)
对于\(30\)%的数据, \(1 ≤ N,M ≤ 10\)
对于\(60\)%的数据, \(1 ≤ N,M ≤ 50\)
对于\(80\)%的数据, \(1 ≤ N,M ≤ 100\)
对于\(100\)%的数据,\(1 ≤ N,M ≤ 200\)
数据已修正,有一些错误的算法(包括部分题解)将不能通过本题。
题解
经典棋盘互吃求最多棋子个数,网络流。
按行的奇偶分组,直接连边即可。
原因:最大流最小割,考虑在这道题中最小割即舍去的棋子。
启示:对抗限制思考最小割对应的意义。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
inline int rd(){
int f=1,j=0;
char w=getchar();
while(!isdigit(w)){
if(w=='-')f=-1;
w=getchar();
}
while(isdigit(w)){
j=j*10+w-'0';
w=getchar();
}
return f*j;
}
const int N=210,M=80000;
int n,m,ban,p[N][N],cnt;
int head[M],las[M],fro[M*5],to[M*5],flo[M*5],tail=1;
int dep[M],s,t,ans;
int X[8]={-1,1,3,3,1,-1,-3,-3};
int Y[8]={3,3,1,-1,-3,-3,-1,1};
inline void adlin(int x,int y,int z){
to[++tail]=y;
fro[tail]=head[x];
head[x]=tail;
flo[tail]=z;
to[++tail]=x;
fro[tail]=head[y];
head[y]=tail;
return ;
}
bool getdep(){
deque<int>lin;
lin.push_back(s);
for(int i=1;i<=cnt;i++)dep[i]=0;
dep[s]=1;
while(!lin.empty()){
int u=lin.front();lin.pop_front();
for(int k=head[u];k;k=fro[k]){
int x=to[k];
if(!flo[k]||dep[x])continue;
dep[x]=dep[u]+1;
lin.push_back(x);
}
}
return dep[t];
}
int getflo(int u,int fl){
if(u==t||!fl)return fl;
int cost=0;
for(int k=las[u];k;k=fro[k],las[u]=k){
int x=to[k],y;
if(!flo[k]||dep[x]<=dep[u])continue;
y=getflo(x,min(fl-cost,flo[k]));
flo[k]-=y,flo[k^1]+=y;
cost+=y;
}
return cost;
}
signed main(){
n=rd(),m=rd(),ban=rd();
ans=n*m;
for(int i=1,x,y;i<=ban;i++)x=rd(),y=rd(),p[x][y]=-1;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(!p[i][j])p[i][j]=++cnt;
else ans--;
}
}
s=++cnt,t=++cnt;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(p[i][j]==-1)continue;
if(i&1)adlin(p[i][j],t,1);
else adlin(s,p[i][j],1);
if(i&1)continue;
for(int k=0;k<8;k++){
int x=i+X[k],y=j+Y[k];
if(x<1||x>n||y<1||y>m||p[x][y]==-1)continue;
adlin(p[i][j],p[x][y],INT_MAX);
}
}
}
while(getdep()){
for(int i=1;i<=cnt;i++)las[i]=head[i];
ans-=getflo(s,INT_MAX);
}
printf("%d",ans);
return 0;
}