标签：10 le 测试点 ... 十月 OIer Tsawke 模拟 tsawke

Tsawke 的十月模拟赛

为了让这场模拟赛只有四道题，所以 T1 和 T2 各自 $ 50\texttt{pts} $，T6 不计入总分！

Std

题目名称	这是一道比原来的T1更像T1的妙妙性质题	最喜欢推柿子了	划水？想屁吃！	什么阴间三元环	嗯？又是data_struct？
题目类型	传统题	传统题	传统题	传统题	传统题
题目目录	intriguing_t1	tomato	escape_from_llq	fxxk_triatomic_ring	d0te__sturct
源程序文件名	intriguing_t1.cpp	tomato.cpp	escape_from_llq.cpp	fxxk_triatomic_ring.cpp	d0te__sturct.cpp
输入文件名	intriguing_t1.in	tomato.in	escape_from_llq.in	fxxk_triatomic_ring.in	d0te__sturct.in
输出文件名	intriguing_t1.out	tomato.out	escape_from_llq.out	fxxk_triatomic_ring.out	d0te__sturct.out
时间限制	1000ms	1000ms	6000ms	1000ms	3000ms
内存限制	1024MiB	1024MiB	1024MiB	1024MiB	512MiB
提交文件限制	100KiB	100KiB	100KiB	100KiB	100KiB
数据组数	10	10	34	10	10
满分分数	50	50	100	100	100

Ex（不计入分数！可以跳，怕你们 AK 之后太无聊）

题目名称	不会有人语法题都切不掉吧？不会吧不会吧？
题目类型	提交答案题
题目目录	grammmmmmmar
源程序文件名	\
输入文件名	\
输出文件名	grammmmmmmar.out
时间限制	\
内存限制	\
提交文件限制	100KiB
数据组数	30
满分分数	0

注意事项

1. 所有文件名均保证为小写（友情提示：请格外注意文件名）。
2. C++ 中 main() 函数返回值必须为 int 且为 $ 0 $。
3. C++ 编译器开启 C++14 标准及 O2 优化。
4. 提交的程序源文件需独立文件夹。
5. 结果比较方式为全文比较（忽略行末空格及行尾回车）。
6. 程序可使用的栈空间限制与对应题目内存限制一致。
7. 评测采用机器配置为：11th Gen Intel(R) Core(TM) i5-11320H @ 3.20GHz。注意：测评将在 Linux 虚拟机中进行，配置会有部分降低，对于造成影响的题目会增加部分时限。
8. 编译选项为：g++ -o sample sample.cpp -lm -Wl,--stack=2147483647 -std=c++14 -O2。
9. 对于本地 Linux 环境下调试时，可以添加编译选项：-fsanitize=undefined,signed-integer-overflow,address 以检测未定义行为、整数溢出，地址越界等问题。
10. 对于提答题请将 .out 为扩展名的文件统一放到子目录下。

这是一道比原来的T1更像T1的妙妙性质题（intriguing_t1）

题目背景

这是一道签到题。

题目描述

我们有如下定义：若在正整数序列 $ A_n $ 中存在若干个连续正整数的和为 $ m $ 的倍数，那么我们称这个正整数序列为“tsawke序列”。

我们给定 $ n, m $，你需要输出任意的长度为 $ n $ 的正整数序列 $ A_n $ 是否均为“tsawke序列”。

tsawke 本来想让你们构造一个具体的方案的，但是考虑到这题如果能想出来做法，方案构造就太简单了（肯定不是因为 tsawke 懒得写 SPJ），于是就变成了判断是否存在。

输入格式

第一行一个整数，表示 $ n $。

第二行一个整数，表示 $ m $。

输出格式

如果成立的话输出 NO，不成立输出 YES。（是的你没看错）

数据范围

对于 Subtask 1(10pts)，满足 $ 1 \le n, m \le 5 $。

对于 Subtask 2(40pts)，满足 $ 1 \le n, m \le 10^{106} $。（是的你也没看错）

保证数字不含前导 $ 0 $。

Examples

Input_1

2 4

Output_1

YES

样例1 说明

存在的反例为序列 $ 1, 2 $。

提示

签到题还想要提示？

最喜欢推柿子了（tomato）

题目背景

tsawke 非常喜欢推式子，但是众所周知 tsawke 太弱了，他经常推不出来式子，现在 tsawke 想请你帮他推式子。

因为这道题是 T1T2，tsawke 又从来不出毒瘤的题，所以 tsawke 为你准备了一些可能用到的公式。

题目描述

对于给定的 $ n, x $，请你求出下式的值：

\[\sum_{k = 0}^{n}\cos(kx) \]

输入格式

第一行两个整数 $ n, x $。

输出格式

一行一个浮点数，表示原式的近似值，误差须在 $ eps = 10^{-5} $ 范围内。

数据范围

对于 $ 20% $ 的数据，满足 $ 1 \le n \le 10^5 $。

对于 $ 100% $ 的数据，满足 $ 1 \le n \le 10^{16}, 1 \le x \le 10 $。

Tips：数据不是很友好。

Examples

Input_1

11451 4

Output_1

1.049856

提示

对于本题我们提供以下公式：

\[e^{ix} = \cos(x) + i\sin(x) \]

\[\dfrac{a + bi}{c + di} = \left( \dfrac{ac + bd}{c^2 + d^2} \right) + \left( \dfrac{bc - ad}{c^2 + d^2} \right) \]

\[\cos(x - y) = \cos(x)\cos(y) + \sin(x)\sin(y) \]

\[\cos(x) - \cos(y) = -2\sin(\dfrac{x + y}{2})\sin(\dfrac{x - y}{2}) \]

对于数列 $ A_n $，若其满足 $ \forall i \in \left[ 1, n - 1 \right], \dfrac{A_{i + 1}}{A_i} = q $，则令 $ S_i = \sum_{j = 1}^{i}A_j $，有 $ S_i = A_1 \times \dfrac{1 - q^i}{1 - q} $。

注意：我们对于结果浮点数的判断会引入 $ eps = 10^{-5} $ 的实数比较，为了防止误差在运算过程中建议但不强行规定使用 __float128，并使用如 cosf128 和 sinf128 等函数，否则可能将无法保证正确性。当你计算得出一个 __float128 类型的变量 ans 时，可以通过如下语句进行输出：

printf("%.6lf\n", (double)ans);

划水？想屁吃！（escape_from_llq）

题目背景

众所周知，在家上网课的时候是划水的好时机，OIer 们也不例外，现在 llq 发现所有 OIer 们都在划水，他想在限制内尽可能多地真实划水中的 OIer，使他们不敢继续划水而去认真上课，但是 llq 不知道最多能真实到多少 OIer，他想请你帮忙计算一下。

题目描述

OIer 们住在一个城市中，这个城市共有 $ n $ 个交通枢纽，整个城市的交通枢纽是联通的（注意并不是任意两个交通枢纽之间都有边相连），每个房间都在两个交通枢纽之间，共有 $ n - 1 $ 个房间，OIer 们都住在房间内，对于房间 $ i $ 存在 $ s_i, t_i, w_i $，表示 $ i $ 号房间在 $ s_i $ 和 $ t_i $ 之间（且 $ s_i, t_i $ 之间是直接连通的），其中有 $ w_i $ 个 OIer。换句话说，整个城市是个树形结构，树上每条边长度相同且都有一个房间，其中有 $ w_i $ 名 OIer。

我们只考虑三天内的情况，每一天中 llq 可以选择一个起点 $ S $ 和终点 $ T $，llq 将会沿着最短路从 $ S $ 走到 $ T $，并真实途径的每一名 OIer。

但是 tsawke 不想太多的 OIer 被抓住，所以每天伊始他会使用 %法 将整个城市的结构，OIer 的数量和分布全部改变，并且令 llq 无法改变路径的起点和终点，而且昨天被真实过的 OIer 今天会重新开始划水，所以 llq 会重新沿着最短路从 $ S $ 走到 $ T $ 并真实途径的学生。

现在你将获得这三天的城市的形态与每个房间的 OIer 数量，你需要帮助 llq 找到一对 $ S, T $ 使 llq 可以在这三天内真实尽可能多的 OIer，并输出最多可以真实的 OIer 数量。

Tips：我们认为任意两个直接连通的交通枢纽之间边的长度是相同的。

输入格式

第 $ 1 $ 行一个整数 $ n $，表示交通枢纽的个数。

第 $ 2 $ 到第 $ n $ 行，每行三个整数 $ s, t, w $，表示第一天城市中 $ s, t $ 之间直接有边相连，且其上有 $ w $ 名 OIer。

第 $ n + 1 $ 到第 $ 2n - 1 $ 行，每行三个整数 $ s, t, w $，表示第二天城市中 $ s, t $ 之间直接有边相连，且其上有 $ w $ 名 OIer。

第 $ 2n $ 到第 $ 3n - 2 $ 行，每行三个整数 $ s, t, w $，表示第三天城市中 $ s, t $ 之间直接有边相连，且其上有 $ w $ 名 OIer。

输出格式

一行一个整数，表示 llq 三天内最多可以真实的 OIer 数量。

数据范围

对于 $ 100% $ 的数据，满足 $ 2 \le n \le 10^5, 0 \le w \le 10^{12}, 1 \le s, t \le n $。

同时我们存在以下几个特殊性质：

特殊性质 $ 0 $：任意两天的城市构成完全相同。

特殊性质 $ 1 $：第二天和第三天的城市构成完全相同。

特殊性质 $ 2 $：对于第二天的每一个交通枢纽，最多只有两个其它交通枢纽有边直接到达它，且编号为 $ x, y $ 的传送站之间有边直接连通充要条件是 $ \vert x - y \vert = 1 $。

特殊性质 $ 3 $：对于第三天的每一个交通枢纽，最多只有两个其它交通枢纽有边直接到达它。

特殊性质 $ 4 \(：\) n \le 3 \times 10^3 $。

子任务序号	总分值	特殊性质
Subtask #1	4	4
Subtask #2	2	0, 1, 2, 3
Subtask #3	6	0, 1
Subtask #4	8	1, 2, 3
Subtask #5	6	1
Subtask #6	6	2, 3
Subtask #7	8	3
Subtask #8	15	None
Subtask #9	15	None(Hack)
Subtask #10	15	None(Hack)
Subtask #11	15	None(Hack)

Tips：存在三组 Hack 数据以防止不优秀的乱搞做法 Accept。

本题共 $ 34 $ 个测试点，每个子任务对应测试点如下：

子任务 $ 1 $ 对应测试点 $ 1-7 $；

子任务 $ 2 $ 对应测试点 $ 8 $；

子任务 $ 3 $ 对应测试点 $ 9-11 $；

子任务 $ 4 $ 对应测试点 $ 12-14 $；

子任务 $ 5 $ 对应测试点 $ 15-17 $；

子任务 $ 6 $ 对应测试点 $ 18-21 $；

子任务 $ 7 $ 对应测试点 $ 22-25 $；

子任务 $ 8 $ 对应测试点 $ 26-31 $；

子任务 $ 9 $ 对应测试点 $ 32 $；

子任务 $ 10 $ 对应测试点 $ 33 $；

子任务 $ 11 $ 对应测试点 $ 34 $；

Examples

Input_1

5
1 2 2
1 3 0
1 4 1
4 5 7
1 2 0
2 3 1
2 4 1
2 5 3
1 5 2
2 3 8
3 4 5
4 5 1

Output_1

27

Input_2 & Output_2

已下发至 /escape_from_llq/examples_2.in，/escape_from_llq/examples_2.out。

样例1 说明

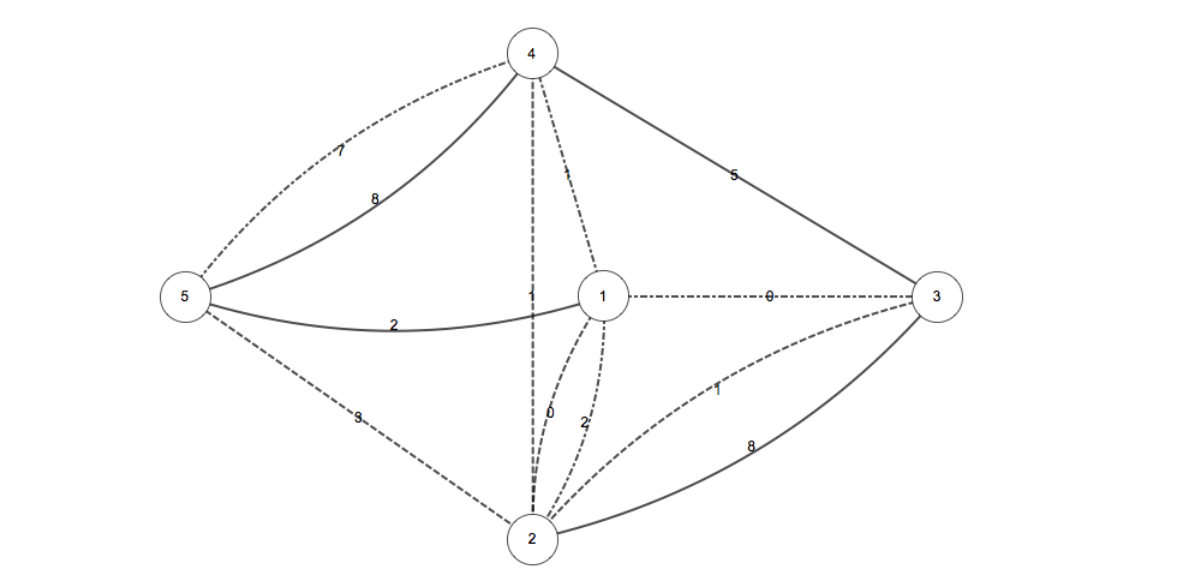
其中点和虚线交替线条、虚线条、实线条，分别表示第一、二、三天的城市结构。

一种最优方案为选择 $ s = 2, t = 5 $，结果为 $ (3) + (8 + 5 + 1) + (2 + 1 + 7) = 27 $。

提示

tsawke 不喜欢虚树，并且虚树看起来很不联赛，所以他并不想让你们用虚树解决这个问题。

什么阴间三元环（fxxk_triatomic_ring）

题目背景

不知道你们是否还记得，tsawke 在讲 LG-P3547 [POI2013]CEN-Price List 的时候提过一点三元环，并讲了一个奇怪的复杂度证明。然后在 sssmzy 讲LG-P3561 [POI2017]Turysta 又提到了竞赛图，那么毒瘤善良的 tsawke 便想考考你，竞赛图中的三元环是否还有什么其它的性质呢？

题目描述

存在一张 $ n $ 个点的有向图，点集为 $ \mathbb{V} $，满足 $ \forall u, v \in \mathbb{V} $，且 $ u \lt v $，则 $ u, v $ 之间有一条从 $ u $ 指向 $ v $ 的边。输出这张图中三元环的数量。

现在我们对这张图进行 $ m $ 次操作，每次操作包含 $ u, v $，且 $ u \neq v $，表示将 $ u, v $ 之间的边反向，每次操作之后你需要再次输出图中三元环的数量。

保证不会出现本质相同的操作，即不会出现 $ u_i = u_{i + 1} \land v_i = v_{i + 1} $ 或 $ u_i = v_{i + 1} \land v_i = u_{i + 1} $。

结果可能过大，对 $ 1145141 $ 取模。

输入格式

第 $ 1 $ 行 $ 2 $ 个整数 $ n, m $。

第 $ 2 - m + 1 $ 行每行 $ 2 $ 个整数，表示 $ u, v $。

输出格式

第 $ 1 $ 行 $ 1 $ 个整数表示原图的三元环数量。

第 $ 2 - m + 1 $ 行每行 $ 1 $ 个整数，对应次操作后图中的三元环数量。

数据范围

对于 $ 10% $ 的数据，满足 $ 2 \le n \le 100, m = 0 $。

对于另外 $ 20% $ 的数据，满足 $ 2 \le n \le 100, 0 \le m \le 10 $。

对于另外 $ 20% $ 的数据，满足 $ 2 \le n \le 400, 0 \le m \le 10^4 $。

对于 $ 100% $ 的数据，满足 $ 2 \le n \le 10^6, 0 \le m \le 10^6 $。

Examples

Input_1

97 10
85 10
89 4
2 75
10 35
91 65
78 80
83 80
15 53
43 90
39 36

Output_1

0
74
158
230
253
278
279
282
319
365
367

嗯？又是data_struct？（d0te__sturct）

题目背景

希望 zpair 这次不会写错文件名。

tsawke 感觉这次的模拟赛出的太简单了，聪明的你们一定在十分钟内就把前四道题都切掉了，为了让聪明的你们能够不至于在剩余的 4h20min 中过于无聊，毒瘤贴心的 tsawke 为你们额外准备了一道“小清新”数据结构~

啊对了，这道题是搬的，然后 emmmmm，原题还有一个很长的奇奇怪怪的题目背景，你们如果无聊也可以看看？？

题目背景之二

众所周知，tsawke 非常懒，以至于他咕掉了很多道题，这些题分为不同的难度，由一个整数描述，当相同难度的题太多时 tsawke 便会彻底放弃这几道题，现在他想请你帮他计算一下最后他最少还需要做多少题。

Tips：略微卡常，别写的太丑就行，也有点卡空间，总之是一道不怎么友好的题。

题目描述

tsawke 已经咕掉了 $ n $ 道题，给定数列 $ a_n $，第 $ i $ 道题的难度为 $ a_i $。

$ q $ 次独立的询问，每次给定 $ l_1, r_1, l_2, r_2, l_3, r_3 $，分别表示三个不交的闭区间，tsawke 会在这三个区间中，将难度相同的题一一对应着彻底咕掉，你需要求出最后还剩下多少道题 tsawke 需要做。

如对于 $ \left[ 1, 1, 1, 2, 2, 3 \right] $， $ \left[ 1, 2, 2, 3, 3, 3 \right] $， $ \left[ 1, 2, 2, 2, 2, 3 \right] $，咕掉的便为 $ \left[ 1, 2, 2, 3 \right] $，在每个区间中去掉这段后剩下的即为答案。

输入格式

第一行两个整数表示 $ n, q $。

第二行 $ n $ 个整数表示 $ a_1, a_2, \cdots, a_n $。

接下来 $ m $ 行每行 $ 6 $ 个整数表示 $ l_1, r_1, l_2, r_2, l_3, r_3 $。

输出格式

共 $ m $ 行，每行一个整数表示对应询问的答案。

Examples

Input_1

5 2
1 2 2 3 3
1 2 2 3 3 4
1 5 1 5 1 5

Output_1

3
0

数据范围

毒瘤题没有部分分。

对于 $ 100% $ 的数据，满足 $ 1 \le n, m \le 10^5, 1 \le a_i \le 10^9, 1 \le l_1, r_1, l_2, r_2, l_3, r_3 \le n, l_1 \lt r_1, l_2 \lt r_2, l_3 \lt r_3 $。

提示

因为这题似乎有一点卡常？复杂度看起来可能不太能过？

所以这里提供一份快读模板：

template < typename T = int >
inline T read(void){
    T ret(0);
    short flag(1);
    char c = getchar();
    while(c != '-' && !isdigit(c))c = getchar();
    if(c == '-')flag = -1, c = getchar();
    while(isdigit(c)){
        ret *= 10;
        ret += int(c - '0');
        c = getchar();
    }
    ret *= flag;
    return ret;
}

当需要读入一个整数时，只需调用 read() 即可返回一个 int 类型的整数，如果需要读入 long long 可调用 read < long long >()。

不会有人语法题都切不掉吧？不会吧不会吧？（grammmmmmmar）

题目背景

（这玩意我第一次做的时候也错了一堆）

众所周知，tsawke 的算法实力非常差，然后 tsawke 发现了一系列的语法辨析题，做完之后发现，tsawke 的语法能力也非常弱，所以毒瘤的 tsawke 也想为难一下聪明的你。

题目描述

本题为提交答案题，仅需提交对应的如 grammmmmmmar1.out 的文件在对应目录下。

对于每个测试点，我们将会给你一段程序，然后你需要不通过辅助工具去手动计算出程序的运行结果（tsawke 相信你们不会在计算机上跑答案的），保证程序中没有难以口算的部分。

对于每段程序，如果可以正常运行你需要将其运行结果写出到对应的 .out 文件中。

若该程序出现了编译错误（Compile Error），那么你不需要输出运行结果，直接输出：This rubbishy programme can not be fxxking compiled at all!。

如果程序出现了未定义行为（Undefined Behavior），直接输出：This rubbishy programme has undefined bahaviors!。

特别地（为了降低难度），对于实现定义行为（IB）和未指明行为（UnsB）我们在这里均按照正常运行处理，即不算做 UB。

Examples

Input_1

// Beginner Level, print the right answer below !
#include <bits/stdc++.h>
using std::cin;
using std::cout;

int main() {
	int x = 10;
	cout << x++ << '\n';
	cout << ++x << '\n';
	return 0;
}

Output_1

10
12

测试点分数

测试点序号	测试点分数
1	0
2	0
3	0
4	0
5	0
6	0
7	0
8	0
9	0
10	0
11	0
12	0
13	0
14	0
15	0
16	0
17	0
18	0
19	0
20	0
21	0
22	0
23	0
24	0
25	0
26	0
27	0
28	0
29	0
30	0

提示

文件均已下发至 /grammmmmmmar/grammmmmmmar*.cpp。

关于 ynoi 的巨长无比的原题目背景

5.632

我（或者是在读这篇文字的你）不属于这个世界

这是世界的界限

6.41

世界的意义必定存在于世界之外

世界中的一切事物如其所存在般而存在，如其所发生般而发生

世界之中不存在价值

——《逻辑哲学论》

我们的情人，不过是随便借个名字，用幻想吹出来的肥皂泡

把信拿去吧，你可以使假戏成真

我本来是无病呻吟，漫无目的的吐露爱情---现在这些漂泊不定的鸟儿有地方栖息了，你可以从信里看出来

拿去吧---由于不是出自真心，话就说得格外动听，拿去吧，就这么办吧...

果然……好女人要有的是，烟、楼顶……还有轻飘飘的衣服呀……

某一天，水上由岐看见天上掉下了个布制玩偶

为了被天空接受而投掷出的她的布偶，不知在天空飞舞了多少次，已经遍体鳞伤

“被天空接受”——那是为了寻找不知何时开始在这个城市流传的“回归天空之路”的行为

为了被天空接受而被扔出去的木偶，在空中飞舞并最终坠落

那是为了将其本身即为世界的少女送予天空的少女的行为

横跨银河，被称作Vega与Altair，或是织女星与牛郎星的两颗星星，再加上北十字星之顶的天鹅座构成了夏之大三角

它被称作譬如三位一体的神圣的图形

只有神圣的图形在天空闪耀之时，世界才与天空相遇

我想试一试，第一次，也是最后一次的恶作剧

那是...什么？

什么事也没有哦，只是，间宫君他自己主动跳下去了而已哦~

怎么回事？

什么事也没有哦，只是，间宫君他自己主动跳下去了而已哦~

但是我看到了，是那个杀死了大家吗？

什么事也没有哦，只是，间宫君他自己主动跳下去了而已哦~

不，那个东西，什么都没有做，只是...

什么事也没有哦，只是，间宫君他自己主动跳下去了而已哦~

只是...怎么回事...

什么事也没有哦，只是，间宫君他自己主动跳下去了而已哦~

我确实听到了头盖骨破碎的声音

但是那个，并非是外面的世界

而是总自己的里面传来的

水上同学...我偶尔会思考这种事情...

世界的极限到底在哪里呢...

世界的...世界的尽头的更尽头...

要是能有那种地方...

要是假如我能够站在那个地方的话...我还是能跟平时一样看着那个尽头的风景吗？我有这种想法....

我理所当然的想着这种事...然后决定似乎是有些奇怪啊

因为那里是世界的尽头哦

是世界的极限哦

如果我能够看到那个的话...世界的极限...是否就等同于我的极限呢？

因为，从那里看到的世界...我所看见的...不就是我的世界吗？

世界的极限...就会变成我的极限吧~

世界就是我看到的摸到的，并且感受到的东西

那样的话，世界到底是什么呢

世界和我到底有什么不同呢...我有这种想法

有吗？

世界和我的差别

是一样的

但是，或许其他人也有相同的感觉...

就连你，或许也认为世界就是你自己吧

并且，我觉得那个大概是正确的...

虽然我不太清楚...大概是你也站在世界的尽头，跟我一样在看着它吧

所以，你也和世界一样

但是啊，那样果然很奇怪啊...

如果世界就是我的话...为什么我会看不到你看到的世界呢？

明明我的世界里有你存在...却看不到你看到的世界

我从来没有看到过你看到的世界

那个，简直就像是两者不会交集的平行宇宙一样...

即使有现象暗示着那个东西存在...却是绝对的无法触碰...

我...看不到你所在的世界...

但是...

那个也是真的是真的吗？

我真的没有看到过你的世界吗...

既然所有的人都平等的拥有她们自己的世界的话

那么为什么世界会变成一个呢？

为什么那么多的世界会存在于这里呢？

世界变成一个的理由

...我偶尔会思考这种事情

所以...我才能够喜欢上你

标签：10,le,测试点,...,十月,OIer,Tsawke,模拟,tsawke
From： https://www.cnblogs.com/tsawke/p/17032833.html