带权并查集
普通的并查集只能维护每个节点所在集合的编号,带权并查集则可以维护集合内任意一点到根的距离。
简单来说,带权并查集支持如下两种操作:
-
在点 \(u\) 和 \(v\) 之间连一条边权为 \(w\) 的边(\(u, v\) 在不同的连通块内)。
-
查询点 \(u\) 与该连通块的根(即并查集的根)的距离。
find
int find(int x)
{
if (f[x] == x)
return x;
int fa = find(f[x]);
dis[x] += dis[f[x]];
return f[x] = fa;
}
f[x]:点 \(x\) 的父亲节点。
dis[x]:点 \(x\) 到其 父亲节点(注意不是根节点)的距离。
请一定注意 dis 数组的定义,如果我们要询问 \(x\) 到根路径的权值和,只需要先调用一遍 find 函数(由于使用了路径压缩,此时 \(x\) 的父亲就为并查集的根)即可。
merge
void merge(int x, int y, int c)
{
int fx = find(x), fy = find(y);
if (fx == fy)
return;
f[fx] = fy, dis[fx] = c + dis[y] - dis[x];
}
merge(x, y, c):在点 \(x\) 和点 \(y\) 直接连一条权值为 \(c\) 的边,同时将 \(x\) 所在的连通块合并到 \(y\) 上。
这里是带权并查集比较难理解的一部分,配合图片食用更加。
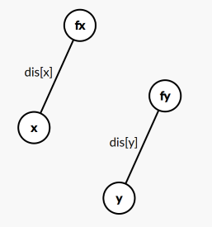
这是初始状态,我们先调用了一次 find(x) 和 find(y),\(x\) 和 \(y\) 所在集合的根以及其到根的距离都已经得到。
我们的任务是在 \(x\) 和 \(y\) 之间连边,但直接修改 f[x] 或 f[y] 都会破坏并查集的结构,因此只能合并 \(fx\) 与 \(fy\)。
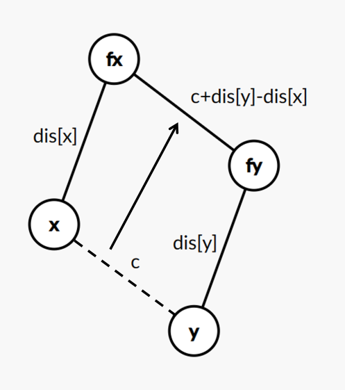
明确一点,根据我的写法,最终集合的根应该为 \(fy\)。所以 \(x\) 到根路径的权值和应为 \(c + dis_y\)(为 \(x \rightarrow y\) 这条边的权值 + \(y\) 到根路径的权值和)。
所以只要在 \(fx\) 和 \(fy\) 之间连一条边权为 \(c + dis_y - dis_x\) 的边,\(x\) 到根的路径和依旧是 \(dis_x + c + dis_y - dis_x = c + dis_y\)。对应的就是将 dis[fx] 的值修改为 \(c + dis_y - dis_x\)。
例题:给定 \(n\) 个变量 \(a_1 \sim a_n\),\(m\) 个约束,每个约束形如 \((x, y, c)\) 表示 \(a_x - a_y = c\),判断是否存在可行解。
解法:把每个约束拆成 \(a_x - a_y \geq c\) 和 \(a_x - a_y \leq c\),就可以用差分约束来解,但可能会被卡到 \(O(nm)\)。如果使用带权并查集来做,则可以在接近线性的时间内解决。
对于每个约束 \((x, y, c)\),分两种情况考虑:
-
若 \(x\) 和 \(y\) 不在同一连通块内,从 \(x\) 向 \(y\) 连一条权为 \(c\) 的边。
-
若 \(x\) 和 \(y\) 在同一连通块内,只要判断 (\(x\) 到根路径权值和) 减去 (\(y\) 到根路径权值和) 是否为 \(c\) 即可。
解法:对于 M i j,从 (\(i\) 所在集合的根) 向 (\(j\) 所在集合的根) 连一条权为 (\(i\) 所在连通块大小) 的边;对于 C i j,输出 \(|\) (\(i\) 到根的权值和) - (\(j\) 到根的权值和) \(|\) 即可。
解法:考虑到 \(A\) 捕食 \(B\),\(B\) 捕食 \(C\),\(C\) 捕食 \(A\),这种循环关系,我们通过在带权并查集中将权值对 3 取模,即可快速判断两者关系。
如果 \(i\) 和 \(j\) 不在同一集合:
-
\(i, j\) 是同类,则从 \(i\) 向 \(j\) 连一条权为 0 的边。
-
\(i\) 捕食 \(j\),从 \(i\) 向 \(j\) 连一条权为 1 的边。
如果 \(i\) 和 \(j\) 在同一集合:
-
\(i, j\) 是同类,则 (\(i\) 到根权值和) 不等于 (\(j\) 到根权值和) 则为假话。
-
\(i\) 捕食 \(j\),则 (\(i\) 到根权值和) - (\(j\) 到根权值和) 不为 1 则为假话。