A cinema has n rows of seats, numbered from 1 to n and there are ten seats in each row, labelled from 1 to 10 as shown in the figure above.
Given the array reservedSeats containing the numbers of seats already reserved, for example, reservedSeats[i] = [3,8] means the seat located in row 3 and labelled with 8 is already reserved.
Return the maximum number of four-person groups you can assign on the cinema seats. A four-person group occupies four adjacent seats in one single row. Seats across an aisle (such as [3,3] and [3,4]) are not considered to be adjacent, but there is an exceptional case on which an aisle split a four-person group, in that case, the aisle split a four-person group in the middle, which means to have two people on each side.
Example 1:
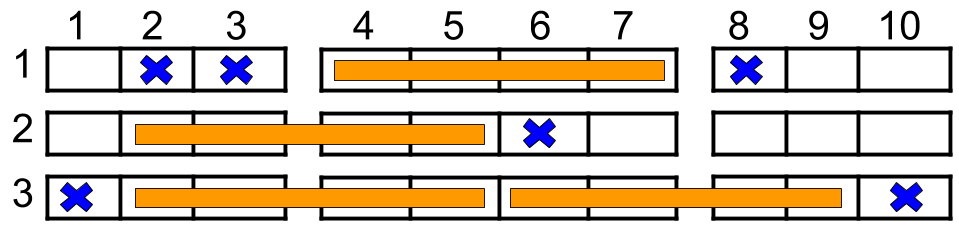
Input: n = 3, reservedSeats = [[1,2],[1,3],[1,8],[2,6],[3,1],[3,10]]
Output: 4
Explanation: The figure above shows the optimal allocation for four groups, where seats mark with blue are already reserved and contiguous seats mark with orange are for one group.
Example 2:
Input: n = 2, reservedSeats = [[2,1],[1,8],[2,6]]
Output: 2
Example 3:
Input: n = 4, reservedSeats = [[4,3],[1,4],[4,6],[1,7]]
Output: 4
Constraints:
1 <= n <= 10^9
1 <= reservedSeats.length <= min(10*n, 10^4)
reservedSeats[i].length == 2
1 <= reservedSeats[i][0] <= n
1 <= reservedSeats[i][1] <= 10
All reservedSeats[i] are distinct.
class Solution:
def maxNumberOfFamilies(self, n, reservedSeats):
res = 0
reservedSeats.sort()
index = 0
row_count = 0
while index < len(reservedSeats):
row = reservedSeats[index][0]
flag1, flag2, flag3 = 1, 1, 1
while index < len(reservedSeats) and reservedSeats[index][0] == row:
seat = reservedSeats[index][1]
if seat in [2, 3, 4, 5]:
flag1 = 0
if seat in [6, 7, 8, 9]:
flag3 = 0
if seat in [4, 5, 6, 7]:
flag2 = 0
index += 1
if flag1 and flag3:
res += 2
elif flag1 or flag2 or flag3:
res += 1
row_count += 1
return res + (n - row_count) * 2