Solved the first five questions with brute force. Still 19 points away from reclaiming purple. Hang on!
Solution: CF1774G Segment Covering
Preface
A brilliant and tricky question (tricky because modding \(998244353\) is 'almost' of no use). This blog is an explanation and extension of the official tutorial.
Notations: We use \([l_i,r_i]\) to denote an interval with index \(i\) (or interval \(i\)) and \([x,y]\) to denote a query interval.
Analysis
The question asks about the difference between the number of ways of covering \([x,y]\) with even and odd numbers of existing intervals. As the question does not ask the numbers of ways with even and odd intervals separately, but the difference between them, we need to fully take advantage of its properties.
Property 1
If an interval contains another interval, i.e. if there exist indices \(i,j\) such that \(l_i\leqslant l_j\leqslant r_j\leqslant r_i,\) or \([l_j,r_j]\subseteq [l_i,r_i],\) then if a covering of \([x,y]\) uses the interval \([l_i,r_i],\) then we may freely choose to use \([l_j,r_j]\) or not, they fall into different categories of even or odd numbers of ways equally, so their net contribution to the final answer is zero. Therefore, we may disregard \([l_i,r_i]\) in our whole process.
After deleting all 'useless' intervals, if we sort the remaining intervals by the left boundary, their right boundary will also be sorted.
Property 2
Suppose \([x,y]\) is the query interval and the intervals \([l_i,r_i]\) are trimmed (by Property 1) and sorted from left to right. Then, the intervals that might have a chance to be chosen are those contained by \([x,y],\) and they are consecutive in the sorted order. We let the list be \(\{[l_i,r_i],[l_{i+1},r_{i+1}],\cdots,[l_{j},r_{j}]\}.\)
If the list is empty or \(l_i\ne x\) or \(r_i<l_{i+1}\) or \(r_j\ne y,\) the answer is obviously \(0.\) So, we suppose \(l_i=x,r_i\geqslant l_{i+1},r_j=y,\) and we know that the interval \([l_i,r_i]\) and \([l_j,r_j]\) must be chosen.
We consider the following case:
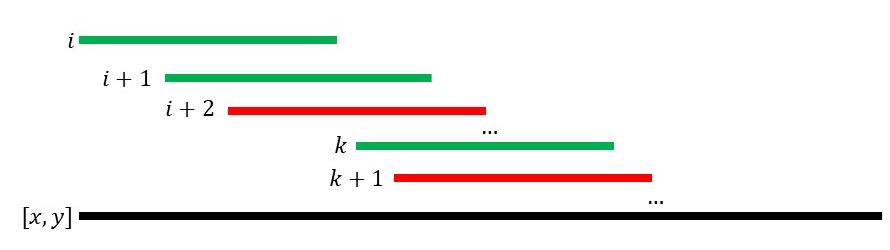
Here, the black line represents the query interval \([x,y],\) and the colored lines are intervals in our list. We know that the interval \(i\) (\([l_i,r_i]\)) must be chosen, so we color it green.
Next, we see that in the picture, \(l_{i+2}\leqslant r_i,\) which means that the interval \(i+2\) intersects with the interval \(i.\) Thus, if we choose the interval \(i+2,\) then whether or not the interval \(i+1\) is chosen does not affect the final union of intervals. Similar to Property 1, this means that if we choose \(i+2,\) the net contribution to the answer is \(0.\) Therefore, the interval \(i+2\) is useless in this case, and we color it red.
Similarly, all the intervals that intersect with the interval \(i\) (except the interval \(i+1\)) are useless. We let the interval \(k\) be the left-most interval that does not intersect with the interval \(i.\)
As we still need to cover \([x,y]\) and the only interval that intersects with \(i\) is \(i+1,\) then we must choose \(i+1,\) and we color it green. Now, as shown in the picture, the interval \(i+1\) is a must-be-chosen interval and \(k\) is a possible interval next to it. In the picture, we may see that \(l_{k+1}\leqslant r_{i+1},\) so the interval \(k+1\) is useless because if we choose \(k+1,\) then we may freely choose \(k\) or not. Similarly, every interval with an index greater than \(k\) that intersects with the interval \(i+1\) is useless, and then \(k\) must be chosen.
To conclude, a must-be-chosen interval and a possible interval next to it make all the other intervals intersecting with the first interval useless, and the second interval must-be-chosen.
From the above statement, we may show inductively that every interval is either must-be-chosen or useless, so there is essentially at most one scheme of choosing the intervals. If there are an even number of intervals in the scheme, the answer is \(1.\) If odd, then \(-1.\) If the must-be-chosen intervals cannot cover \([x,y]\), then the answer is \(0.\) The scheme is like the following:

Note that we split the intervals into two "layers," and for every interval, only the intervals next to it intersect with it. In this picture, the interval \(j\) is colored yellow, with the same color as \(i+1,\) so there are an even number of intervals and the answer is \(1.\) If \(j\) is colored green, the answer becomes \(-1.\)
A Hidden Tree Structure
Property 2 already gives us a method of finding a scheme of choosing intervals for a given query interval \([x,y],\) which is recursively seeking the must-be-chosen intervals and deleting useless intervals until there is no interval to add (\(0\)) or \(y\) is reached (\(\pm 1\)). However, as there are many queries, we need to optimize that.
Let's look closer at the picture above. The intervals are divided into two layers, one starting with \(i\) and another starting with \(i+1.\) Also, for every interval, if it is not the end, its next interval on the same layer is always the interval on its right that is disjoint with it.
Therefore, if we link each interval to the interval on its right that is disjoint with it, a tree structure emerges before our eyes. To make it easy to implement, we link all the intervals that have no "parents" to a virtual root node.
This leads to our final "theorem" of the question:
\(\text{Theorem. }\)There is a scheme of choosing the interval if and only if the interval \(j\) is the ancestor of exactly one of \(i\) and \(i+1.\) If it is the ancestor of \(i,\) then the answer is \(-1.\) If \(i+1,\) then the answer is \(1.\)
\(\text{Note. }\)Please prove this theorem independently. There are two points worth noting. Firstly, if \(j\) is the common ancestor of both \(i\) and \(i+1,\) then there is one point where both green and yellow intervals are disjoint with \(j,\) so the interval \([x,y]\) cannot be fully covered. Secondly, the official tutorial derives the answer \(\pm 1\) by counting the number of intervals used, but actually, we only need to check whose ancestor \(j\) is. (see the picture above)
Implementation
A trick of STL set: removing 'useless' intervals by Property 1
If an input interval contains another, we remove the larger one.
This can be done in multiple ways, we may sort the intervals in some manner and label the useless intervals, which is the method in the official tutorial.
Here is another way: we may maintain a set of intervals such that no interval is contained by another, through a specifically designed \(<\) relation.
We define that the intervals \([l_1,r_1]<[l_2,r_2]\) if \(l_1<l_2\) and \(r_1<r_2.\) We may see that if an interval contains another, they are considered 'equal' by set (because neither \(<\) nor \(>\)).
The algorithm is: When we try to add \([l,r]\) into the set, we use find() method to look for the interval that is 'equal' to \([l,r].\) If it does not exist, then we simply insert \([l,r]\) into the set.
Suppose it is \([a,b].\) If \([l,r]\) contains \([a,b],\) then we discard \([l,r].\)
Lastly, if \([a,b]\) contains \([l,r],\) then we remove \([a,b]\) from the set and check if there are other intervals in the set that contains \([l,r].\) After removing all of them, we insert \([l,r].\)
Looking for 'parents'
We may use vector to store and index the ordered intervals remaining in the set. Now, for an interval \([l_i,r_i]\), its 'parent' is the first interval to its right that is disjoint to it. We may use bisection or two-pointers to achieve this. Here is another way:
We may still use STL and the \(<\) relation we have designed. For the interval \([l_i,r_i],\) its 'parent' \([l_k,r_k]\) is exactly the first interval 'greater than' \([r_i,r_i],\) which may be found by upper_bound.
Similarly, we may use upper_bound to find the left-most interval for the query \([x,y],\) which is the first interval 'greater than' \([x-1,x-1].\)
Checking ancestors
Note that we need to check whether the interval \(j\) (defined as the unique interval \([l_j,r_j]\) such that \(r_j=y\)) exists and is the ancestor of \(i\) or \(i+1.\) This can be done by binary lifting, the method for LCA. Starting from node \(i\) (or \(i+1\)), we lift it to the last interval with its right boundary \(\leqslant y.\) Then, if its right boundary \(=y,\) then it is interval \(j\) and an ancestor of \(i\) (or \(i+1\)).
Code
Here is a sample code integrating all the ideas above. The binary-lifting array is f and the vector v stores all non-useless intervals in order, with indices from \(0\) to v.size()-1. We let v.size() be the index of the virtual node.
We use li to denote the first interval with its left-boundary \(\geqslant x.\) Then, if it does not exist, or its left-boundary is not \(x,\) or its right-boundary exceeds \(y,\) the answer is \(0.\) If the interval li is equal to \([x,y],\) the answer is \(-1.\)
Excluding all the cases above, li is just the interval \(i\) in our analysis section, and our second interval is just li+1. There are some special cases to deal with. Please read the code and make sure you understand all the special cases.
//This program is written by Brian Peng.
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define Rd(a) (a=rd())
#define Gc(a) (a=getchar())
#define Pc(a) putchar(a)
int rd(){
int x;char c(getchar());bool k;
while(!isdigit(c)&&c^'-')if(Gc(c)==EOF)exit(0);
c^'-'?(k=1,x=c&15):k=x=0;
while(isdigit(Gc(c)))x=x*10+(c&15);
return k?x:-x;
}
void wr(int a){
if(a<0)Pc('-'),a=-a;
if(a<=9)Pc(a|'0');
else wr(a/10),Pc((a%10)|'0');
}
signed const INF(0x3f3f3f3f),NINF(0xc3c3c3c3);
long long const LINF(0x3f3f3f3f3f3f3f3fLL),LNINF(0xc3c3c3c3c3c3c3c3LL);
#define Ps Pc(' ')
#define Pe Pc('\n')
#define Frn0(i,a,b) for(int i(a);i<(b);++i)
#define Frn1(i,a,b) for(int i(a);i<=(b);++i)
#define Frn_(i,a,b) for(int i(a);i>=(b);--i)
#define Mst(a,b) memset(a,b,sizeof(a))
#define File(a) freopen(a".in","r",stdin),freopen(a".out","w",stdout)
#define N (200010)
int m,q,x,y,f[N][20];
struct T{int l,r;
bool operator<(T b)const{return l<b.l&&r<b.r;}
};//The structure of intervals, with < relation defined.
set<T>st;
signed main(){
Rd(m),Rd(q);
while(m--){
Rd(x),Rd(y);
auto it(st.find({x,y}));//Find the interval in the set that contains
//or is contained by the input [x,y]
if(it==st.end())st.insert({x,y});
else if(x<=it->l&&it->r<=y)continue;//[x,y] contains a smaller interval
else{
st.erase(it);//[x,y] is contained by a larger interval
while((it=st.find({x,y}))!=st.end())st.erase(it);
//Remove all the intervals that contain it
st.insert({x,y});
}
}
vector<T>v(st.begin(),st.end());
Frn0(i,0,v.size())
*f[i]=upper_bound(v.begin()+i+1,v.end(),T({v[i].r,v[i].r}))-v.begin();
//Use upper_bound and < relation to find the parent node
int lg(log2(v.size()));
*f[v.size()]=v.size();
Frn1(j,1,lg)Frn1(i,0,v.size())f[i][j]=f[f[i][j-1]][j-1];//binary lifting
while(q--){
Rd(x),Rd(y);
int li(upper_bound(v.begin(),v.end(),T({x-1,x-1}))-v.begin());
//li is the index of the first interval with left boundary >= x
if(li==v.size()||v[li].l!=x||v[li].r>y){wr(0),Pe;continue;}
//Special cases: li not existing, li not covering x, li exceeding y
if(v[li].r==y){wr(998244352),Pe;continue;}
//Special case: li is just [x,y]
if(li+1==v.size()||v[li+1].r>y||v[li+1].l>v[li].r){wr(0),Pe;continue;}
//Special cases concerning li+1
int u(li),u2(li+1);
Frn_(i,lg,0)if(f[u][i]<v.size()&&v[f[u][i]].r<=y)u=f[u][i];
Frn_(i,lg,0)if(f[u2][i]<v.size()&&v[f[u2][i]].r<=y)u2=f[u2][i];
//Binary lifting li and li+1 to the last intervals with right-boundary <= y
if(u==u2||v[u].r!=y&&v[u2].r!=y)wr(0),Pe;
//Common ancestor or both not reaching y
else if(v[u].r==y)wr(998244352),Pe;//Ancestor of li
else wr(1),Pe;//Ancestor of li+1.
}
exit(0);
}
Time Complexity: \(O((m+q)\log m)\)
Memory Complexity: \(O(m\log m)\)
Extension
STL is a very powerful tool.
In this question, we use STL set to maintain a set of intervals that one does not contain another, but a specifically designed \(<\) relation.
By designing different \(<\) relations, we may maintain a set of intervals with different properties conveniently. For example, my blog
Solution: CF731D 80-th Level Archeology -- Letter, Interval, and Reverse Thinking
solves another CF problem by maintaining a set of mutually disjoint intervals by defining another \(<\) relation between intervals.
Thanks for reading! See you next round!
标签:set,CF1774G,interval,Solution,li,intervals,answer,Segment,its From: https://www.cnblogs.com/BrianPeng/p/17006947.html