RationalLee
样例 #1
样例输入 #1
3
4 2
1 13 7 17
1 3
6 2
10 10 10 10 11 11
3 3
4 4
1000000000 1000000000 1000000000 1000000000
1 1 1 1
样例输出 #1
48
42
8000000000
分析：
对每个人尽量取更大的数，对每个要取数不管是先去还是后取，对答案的贡献是一样的，每个人从大往小取，分别计算答案
点击查看代码
bool cmp(int a, int b)
{
return a > b;
}
void solve()
{
res = 0;
cin >> n >> k;
for (int i = 1; i <= n; i++)
cin >> a[i];
for (int i = 1; i <= k; i++)
cin >> w[i];
sort(a + 1, a + 1 + n, cmp);
sort(w + 1, w + 1 + k);
int idx = 0; // 直接取需要的最小的数
for (int i = 1; i <= k; i++)
{
if (w[i] == 1)
res += a[i] * 2;
else
{
idx += w[i] - 1;
res += a[i];
res += a[k + idx];
}
}
cout << res << endl;
}
TediousLee
题面翻译
首先，我们定义 RDB 为一棵具有特殊性质的树，它有一个级别 level。
一个级别为 1 的 RDB 是一个单独的节点。
接着，对于所有 i>1，级别为 i 的 RDB 的构成方法如下。
先求出级别为 i-1 的 RDB，然后对于该 RDB 中的每个节点 x。
- 如果 x 没有孩子，那么给他加上一个孩子。
- 如果 x 只有一个孩子，那么给他加上两个孩子。
- 如果 x 已经有了超过一个孩子，那么我们跳过节点 x。
接下来，我们定义一个 claw （见下图），它也是一棵具有特殊性质的树，并且将节点 $1$ 称为这个 claw 的中心，其他的称为底部节点。
现在，给出一个级别为 n 的 RDB，初始时他上面的所有节点都为绿色，你可以进行一些操作。
对于每次操作，你需要在给出的 RDB 中找到一个 claw，满足所有底部节点在 RDB 中都是中心节点的儿子，且这四个节点在 RDB 中都是绿色。然后将这四个节点染为黄色。
问最多可以将多少个节点染成黄色。
样例 #1
样例输入 #1
7
1
2
3
4
5
100
2000000
样例输出 #1
0
0
4
4
12
990998587
804665184
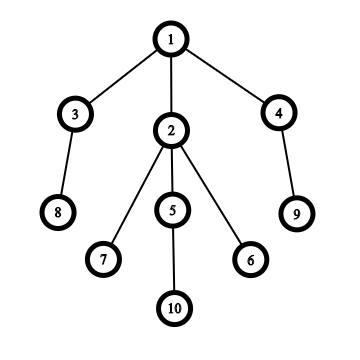Rooted Dead Bush of level 4.
分析：
对于层数为n的树，根节点的三个子节点中，左右子树为n-2，中间子树为n-1; 所以初步递推为f(n) = f(n - 1) + 2 * f(n - 2);当根节点为3的倍数时候，根节点与其三个子节点可以染色形成一组claw
点击查看代码
void init()
{
for (int i = 3; i < N; i++)
{
f[i] = (f[i - 1] + 2 * f[i - 2] % MOD) % MOD;
if (i % 3 == 0)
f[i]++;
f[i] %= MOD;
}
}
void solve()
{
cin >> n;
cout << f[n] * 4 % MOD << endl;
}
DeadLee
题面翻译
Lee 为客人们准备了 n 种菜品，其中第 i 种菜品有wi份。Lee 有 m 位客人，每位客人都喜欢吃恰好两种菜品，第 i 位客人喜欢的菜品种类为 xi,yi。
Lee 的客人们将排成一队依次用餐。对于当前用餐的客人，对于所有他喜欢且还有剩余的菜品，这位客人会吃掉一份该菜品。如果他喜欢的所有种类都已经吃完了，他会愤怒地把 Lee 吃掉。
Lee 希望你帮他安排客人的次序来保证自己的生命安全，或者说明 Lee 一定会被吃掉。
题目描述
样例 #1
样例输入 #1
3 3
1 2 1
1 2
2 3
1 3
样例输出 #1
ALIVE
3 2 1
样例 #2
样例输入 #2
3 2
1 1 0
1 2
1 3
样例输出 #2
ALIVE
2 1
样例 #3
样例输入 #3
4 4
1 2 0 1
1 3
1 2
2 3
2 4
样例输出 #3
ALIVE
1 3 2 4
样例 #4
样例输入 #4
5 5
1 1 1 2 1
3 4
1 2
2 3
4 5
4 5
样例输出 #4
ALIVE
5 4 1 3 2
样例 #5
样例输入 #5
4 10
2 4 1 4
3 2
4 2
4 1
3 1
4 1
1 3
3 2
2 1
3 1
2 4
样例输出 #5
DEAD
分析：
可以先计算每一种菜品有多少人喜欢，在这些菜品中如果需要数≤该菜品的总数，那么喜欢这些菜品的人不管安排什么顺序都可以有菜品吃，就可以直接把这一类人放在最后讨论，
首先讨论他们喜欢的另一件菜品，对于这些菜品：
- 如果需求数
≤总数，同样加入后讨论的队列中去 - 如果需求数
＞总数- 如果该同学已经入队，就不会再消耗该菜品，当前菜品的需求--；
- 如果该同学未入队，就会消耗当前菜品，
显然我们只会对第一种情况的同学进行贪心讨论
实现的方法类似拓扑排序
参考资料CSDN
点击查看代码
int sum[N], need[N];
int h[N], e[N], ne[N], idx;
int ds[N];
bool st[N];
vector<int> res;
queue<int> q;
struct P
{
int a, b;
} p[N];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
void solve()
{
mst(h, -1);
cin >> n >> m;
for (int i = 1; i <= n; i++)
cin >> sum[i];
for (int i = 1, a, b; i <= m; i++)
{
cin >> a >> b;
p[i] = {a, b};
add(a, i), add(b, i);
ds[a]++, ds[b]++; // 需求++
}
for (int i = 1; i <= n; i++)
if (ds[i] <= sum[i])
q.push(i); // 这些人的菜品贪心讨论
while (q.size())
{
int t = q.front();
q.pop();
for (int i = h[t]; ~i; i = ne[i])
{
int j = e[i];
if (st[j])
continue;
st[j] = true;
res.push_back(j);
int tmp = p[j].a;
if (tmp == t)
tmp = p[j].b;
if (--ds[tmp] <= sum[tmp])
q.push(tmp);
}
}
if (res.size() != m)
cout << "DEAD" << endl;
else
{
cout << "ALIVE" << endl;
for (int i = res.size() - 1; i >= 0; i--)
cout << res[i] << ' ';
cout << endl;
}
}