题目描述
给定一个无向简单图 \(G\),统计有多少个点对 \((u, v)\) 满足:
- \(u, v\) 之间没有边直接连接:\((u, v) \notin \text E\)
- 连接 \((u, v)\) 后 \(G\) 是
二分图一个无向图被称为二分图,当且仅当可以将每个顶点涂成黑色或白色且满足以下条件:
- 没有边连接以相同颜色的顶点。
思路
什么时候 D题 也开始考图论了
不妨先对原图进行染色
bool dfs(int p, int c)
{
color[p] = c;
for (auto i : g[p]) // vector存图
{
if (!color[i])
if (!dfs(i, 3 - c))
return 0;
else if (color[i] == c)
return 0;
}
return 1;
}
假如我们得到了这样的图(样例1):
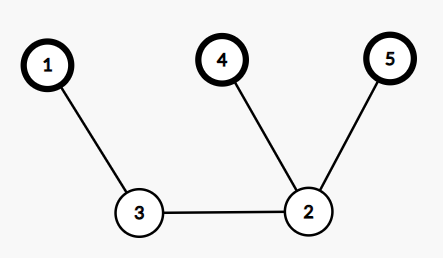
此时有两种情况:
- 原图不是二分图,输出
0; - 如果要进行连边,为了保持原图二分图的特性,只能连接异色两点。
于是答案就是:异色点对的数量
所以我们只需要统计有多少两个异色点就可以了——
\(\huge吗!?\)
如果你这么想就太天真了,看下面这个 \(\texttt{hack}\):
10 1
1 2
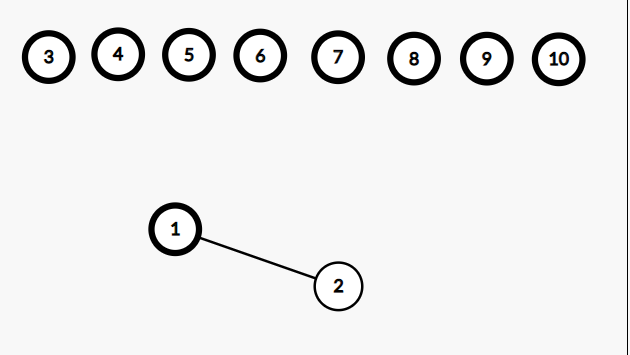
此时你不知道那些孤立的点该如何染色,如果随便染一个颜色的话会漏情况。
如何解决??
反向考虑问题:
最终答案 = 所有情况 - 不可能情况
- 所有情况:\(\dfrac{n(n-1)}{2} - m\),所有可能的连边减去已经连上的边。
- 不可能情况:\(\dfrac{cnt_1(cnt_1-1)}{2} + \dfrac{cnt_2(cnt_2-1)}{2}\) 两种颜色集合内部连边
这样就自动计算了那些漏掉的情况
码来!
// Problem: D - Make Bipartite 2
// Contest: AtCoder - HHKB Programming Contest 2022 Winter(AtCoder Beginner Contest 282)
// URL: https://atcoder.jp/contests/abc282/tasks/abc282_d
// Memory Limit: 1024 MB
// Time Limit: 2000 ms
// Author: Moyou
// Copyright (c) 2022 Moyou All rights reserved.
// Date: 2022-12-17 20:28:38
#include <algorithm>
#include <cstring>
#include <iostream>
using namespace std;
const int N = 1e6 + 10;
vector<int> g[N];
int color[N];
int cnt1, cnt2, ans;
bool flg = 1;
bool dfs(int p, int c) // 染色法
{
color[p] = c;
if (c == 1)
cnt1++; // 统计黑白色点的个数
else
cnt2++;
for (auto i : g[p])
if (!color[i] && !dfs(i, 3 - c) || color[i] == c)
return 0;
return 1;
}
int main()
{
int n, m;
cin >> n >> m;
for (int i = 1; i <= m; i++)
{
int a, b;
cin >> a >> b;
g[a].push_back(b);
g[b].push_back(a);
}
ans = n * (n - 1) / 2 - m;
for (int i = 1; i <= n; i++)
{
if (color[i] == 0) // 如果未染色,表明这是一个新连通块
{
cnt1 = cnt2 = 0; // 记得重置
flg &= dfs(i, 1); // 为什么是 &= ?
// 只要有一个连通块不是二分图,全图就不是二分图
ans -= (cnt1 - 1) * cnt1 / 2 + (cnt2 - 1) * cnt2 / 2;
}
}
if (!flg)
puts("0");
else
cout << ans << endl;
return 0;
}