前面写过一篇傅里叶变换的文章:
https://zhuanlan.zhihu.com/p/66117227
但是在工程应用中,得益于数字技术的应用,绝大多数傅里叶变换的应用都是采用离散傅里叶变换(DFT),更确切的说,是它的快速算法FFT。这篇文章再来写写有关离散傅里叶变换的关键点。
闲言少叙,直入主题。先把DFT的式子写在这里:

对离散傅里叶变换变换,我认为最重要的是搞清楚两点:




最后结合一个实例来加深上述对离散傅里叶变换的结果的理解。
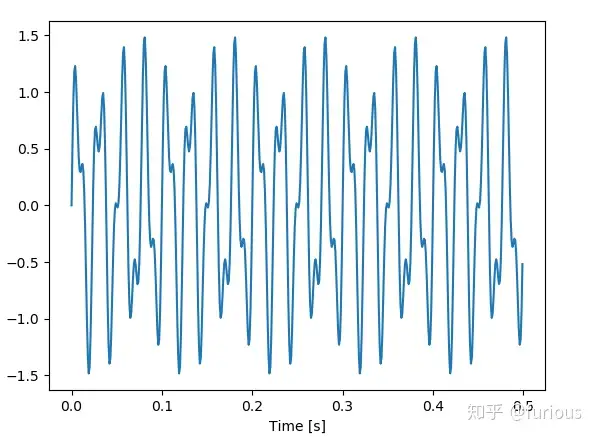
假设原始信号:
,即40Hz和90Hz两个正弦信号的叠加。来看看不同采样过程得到的DFT(FFT)结果。
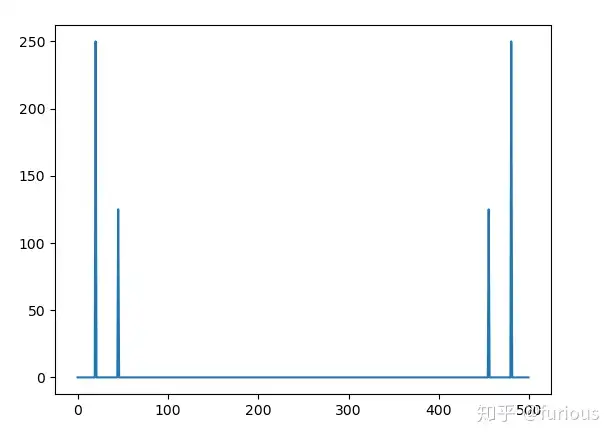
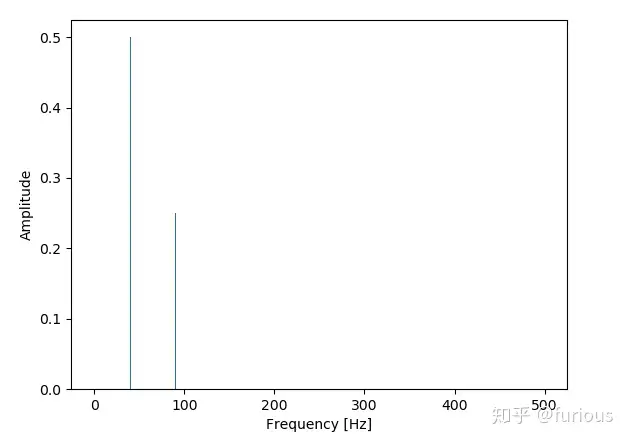
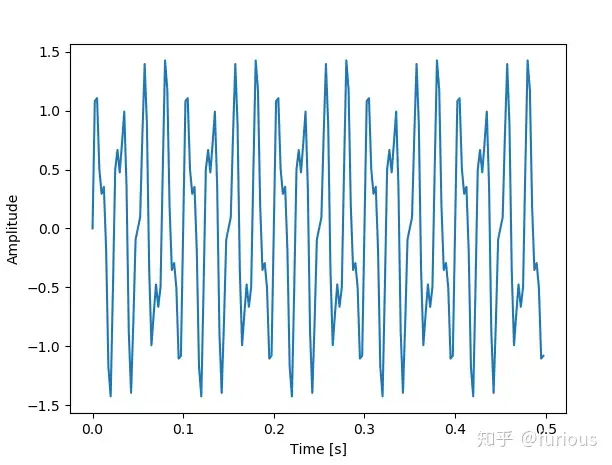
1、在0~0.5s内采样500点得到
,即采样频率为。
Sample rate: 1000.0 Hz
Samples size: 500
Value at index 0: (-4.032691340321753e-14+0j)
Value at index 1: (5.47331447460053e-14-2.3037127760972e-15j)
Value at index 499: (5.4687509286977934e-14-6.571937883535803e-17j)
Value at index 2: (7.420972054685959e-14+2.728368124174801e-14j)
Value at index 498: (7.420972054685959e-14-2.7283681241748016e-14j)
Value at index 3: (8.290505399586863e-14-7.652212197228891e-14j)
Value at index 497: (8.358757983676411e-14+7.495170765863399e-14j)
Value at index 4: (1.1677769275717452e-13+1.3442578178785925e-13j)
Value at index 496: (1.1677769275717452e-13-1.3442578178785925e-13j)
Value at index 17: (-7.504531301157937e-14+1.2723135031031761e-14j)
Value at index 483: (-7.672049076101245e-14-1.500632837960154e-14j)
Value at index 18: (-7.891238745560246e-15+6.78774432759792e-14j)
Value at index 482: (-7.89123874556022e-15-6.787744327597919e-14j)
Value at index 19: (-2.5937242233361435e-14+2.4704194714533472e-14j)
Value at index 481: (-2.4853927632423113e-14-2.2714218335194713e-14j)
Value at index 20: (-2.5969976162903077e-13-249.99999999999997j)
Value at index 480: (-2.7020071315753276e-13+249.99999999999994j)
Value at index 21: (-1.0514300973234786e-13-1.0006753400743443e-13j)
Value at index 479: (-1.0455557375562673e-13+9.966632961798892e-14j)
Value at index 22: (4.27052642300047e-14-7.30154103729329e-14j)
Value at index 478: (4.2705264230004636e-14+7.301541037293293e-14j)
Value at index 23: (-7.27269879933383e-14-2.603104120782442e-15j)
Value at index 477: (-7.12935306401559e-14-1.3354376259863072e-15j)
Value at index 42: (-3.1818051957819556e-13+1.1687262563911411e-13j)
Value at index 458: (-3.1818051957819556e-13-1.168726256391141e-13j)
Value at index 43: (-5.450564689264658e-14-1.1722764422956276e-13j)
Value at index 457: (-5.314929135111624e-14+1.1522778100403543e-13j)
Value at index 44: (7.675296751851385e-15+5.02082399689537e-14j)
Value at index 456: (7.675296751851395e-15-5.02082399689537e-14j)
Value at index 45: (-1.8656042783807358e-13-125.00000000000001j)
Value at index 455: (-1.8283507960060743e-13+125j)
Value at index 46: (2.9414340906931243e-14-2.8748428671670603e-15j)
Value at index 454: (2.9414340906931256e-14+2.8748428671670793e-15j)
Value at index 47: (-1.5607886375281088e-13+1.515599634511694e-13j)
Value at index 453: (-1.5622888838206788e-13-1.5231699611378945e-13j)
Value at index 48: (-3.336736633940097e-13-1.8468226362166973e-13j)
Value at index 452: (-3.336736633940097e-13+1.846822636216697e-13j)
根据
,40Hz对应的点应该是40x500/1000 = 20,90Hz对应的点是90x500/1000 = 45。仔细看上面的结果,峰值就出现在20和45这两个X[k]上,与上面的结果是相符的。
2、在0~0.5s内采样200点。即采样频率为
。
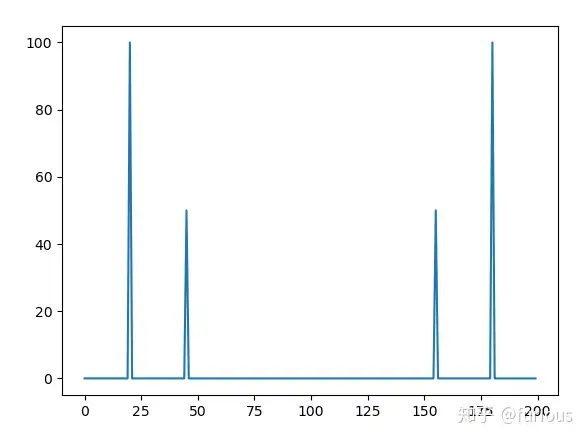
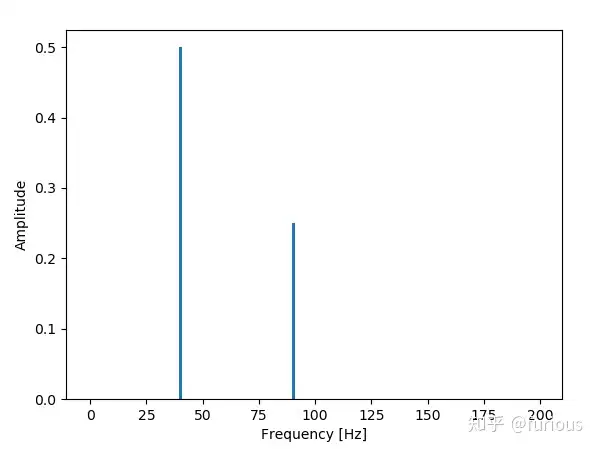
Sample rate: 400.0 Hz
Samples size: 200
Value at index 0: (-9.962313679719496e-15+0j)
Value at index 1: (1.5375738523043498e-14-1.7763568394002505e-14j)
Value at index 199: (1.5364526984141232e-14+1.8053874443897092e-14j)
Value at index 2: (2.4360703442280214e-14+2.0532966203745806e-14j)
Value at index 198: (2.4360703442280205e-14-2.053296620374579e-14j)
Value at index 3: (2.0288475407009816e-14-2.8199664825478976e-14j)
Value at index 197: (2.0807016603803593e-14+2.5781191134887997e-14j)
Value at index 4: (2.3558454288221e-14+5.100011152372421e-14j)
Value at index 196: (2.4588961133289312e-14-5.06542319400188e-14j)
Value at index 17: (-4.948158073846615e-14-2.3807485819200347e-15j)
Value at index 183: (-4.947317469249361e-14+2.3489297141087214e-15j)
Value at index 18: (7.562557031226013e-15+3.176911129338048e-14j)
Value at index 182: (7.562557031225999e-15-3.176911129338048e-14j)
Value at index 19: (-1.6223568883664007e-14+1.01840359973437e-14j)
Value at index 181: (-1.5700099313549882e-14-1.1498463655640398e-14j)
Value at index 20: (-1.1820905858067227e-13-99.99999999999997j)
Value at index 180: (-1.0938604556396042e-13+99.99999999999997j)
Value at index 21: (-1.1620694421953064e-13-4.751106283246057e-14j)
Value at index 179: (-1.150784893098272e-13+4.793037226530092e-14j)
Value at index 22: (1.6099799689737958e-14-1.3271426343635642e-13j)
Value at index 178: (1.6099799689737958e-14+1.327142634363564e-13j)
Value at index 23: (3.73441643855716e-14+5.0081735226909336e-15j)
Value at index 177: (3.687933703385216e-14-4.471625968067038e-15j)
Value at index 42: (-1.1557943305798278e-13+5.097782982384095e-14j)
Value at index 158: (-1.1557943305798278e-13-5.097782982384095e-14j)
Value at index 43: (-1.8613645616263873e-15-3.443876516418567e-14j)
Value at index 157: (-2.457778623388092e-15+3.637881588990269e-14j)
Value at index 44: (-6.6130108234333566e-15-3.4073835405877573e-15j)
Value at index 156: (-5.653045149440138e-15+8.341216716228753e-16j)
Value at index 45: (-6.686373773508564e-14-50j)
Value at index 155: (-6.667221489155492e-14+50j)
Value at index 46: (2.1890070028903165e-14+2.1251334251785863e-15j)
Value at index 154: (2.1890070028903178e-14-2.1251334251785784e-15j)
Value at index 47: (-6.374431304487239e-14+6.92901767459968e-14j)
Value at index 153: (-6.42527926289295e-14-7.005184499916765e-14j)
Value at index 48: (-1.2160331765013047e-13-6.524217072453415e-14j)
Value at index 152: (-1.2160331765013047e-13+6.524217072453417e-14j)
同样根据
,40Hz对应的点应该是40x200/400 = 20,90Hz对应的点是90x200/400 = 45。与上面的结果是相符的。
3、在0~0.2s内采样200点。即采样频率还是
。
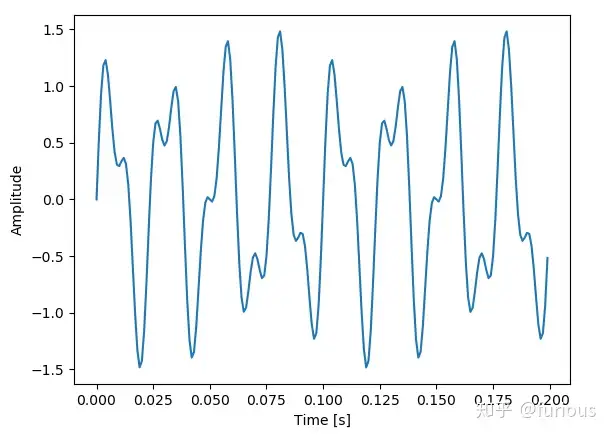
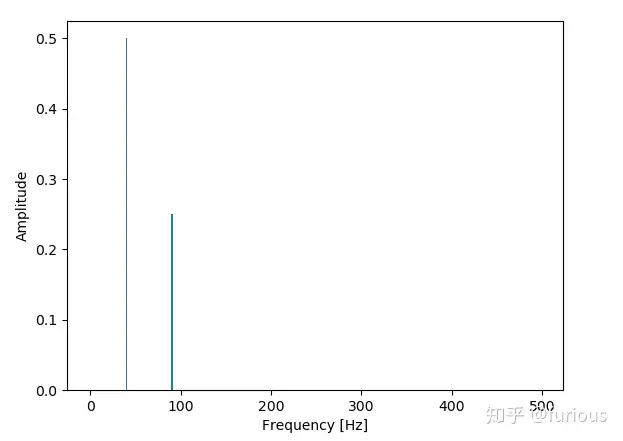
Sample rate: 1000.0 Hz
Samples size: 200
Value at index 0: (-4.3026244412314335e-14+0j)
Value at index 1: (1.173774221692321e-14-2.2886577640004618e-14j)
Value at index 199: (1.1737742216923204e-14+2.2886577640004624e-14j)
Value at index 2: (5.218512159071522e-14-1.0547118733938987e-15j)
Value at index 198: (5.304654765694656e-14+3.6369492074111756e-16j)
Value at index 3: (-1.717798331659063e-14+4.185135291056711e-14j)
Value at index 197: (-1.7177983316590625e-14-4.185135291056711e-14j)
Value at index 4: (6.752817999010086e-15-7.897865029439045e-15j)
Value at index 196: (6.752817999010086e-15+7.897865029439045e-15j)
Value at index 5: (5.46586736889134e-16+3.113498085620893e-14j)
Value at index 195: (5.46586736889132e-16-3.113498085620893e-14j)
Value at index 6: (8.664379025409079e-15+2.886579864025407e-14j)
Value at index 194: (8.122427615151029e-15-2.8218391464038713e-14j)
Value at index 7: (-3.1583155825707856e-14+3.1187715085989398e-15j)
Value at index 193: (-3.158315582570786e-14-3.1187715085989386e-15j)
Value at index 8: (-7.430325360934045e-14-100.00000000000001j)
Value at index 192: (-7.110724204215482e-14+100.00000000000001j)
Value at index 9: (-2.6730839326555293e-14-2.0006065544472292e-14j)
Value at index 191: (-2.6730839326555293e-14+2.0006065544472292e-14j)
Value at index 10: (-7.856970190857711e-15-4.343435848423759e-14j)
Value at index 190: (-6.518294109116255e-15+4.7989777969450694e-14j)
Value at index 11: (9.453254387832055e-15-6.769310470798414e-14j)
Value at index 189: (9.453254387832046e-15+6.769310470798417e-14j)
Value at index 12: (5.275563422093338e-14-2.9657914357409356e-14j)
Value at index 188: (5.275563422093339e-14+2.9657914357409356e-14j)
Value at index 13: (6.50781429135821e-15-3.123232760292878e-14j)
Value at index 187: (6.507814291358213e-15+3.1232327602928776e-14j)
Value at index 14: (8.196767977858568e-14-1.2315620899056779e-14j)
Value at index 186: (8.147505297942633e-14+1.2222322554793413e-14j)
Value at index 15: (5.5154619065607806e-14+4.022254205534508e-14j)
Value at index 185: (5.5154619065607806e-14-4.022254205534508e-14j)
Value at index 16: (2.4752813406175686e-14+4.0258097738867185e-14j)
Value at index 184: (2.475281340617569e-14-4.025809773886718e-14j)
Value at index 17: (-1.0398979154998123e-14+4.1019175485025494e-14j)
Value at index 183: (-1.039897915499813e-14-4.101917548502549e-14j)
Value at index 18: (-4.4486770345657527e-14-50.00000000000001j)
Value at index 182: (-4.328485467007317e-14+50j)
Value at index 19: (-3.0147506558109117e-14-2.4004792372941166e-14j)
Value at index 181: (-3.014750655810912e-14+2.4004792372941175e-14j)
Value at index 20: (4.3617316218763913e-14-4.293074786291573e-14j)
Value at index 180: (4.3617316218763913e-14+4.2930747862915725e-14j)
同样根据
,40Hz对应的点应该是40x200/1000 = 8,90Hz对应的点是90x200/1000 = 18。与上面的结果是相符的。
文章链接 https://zhuanlan.zhihu.com/p/71582795
标签:index,13,15,14,DFT,Value,离散,14j,傅里叶 From: https://www.cnblogs.com/fpga-notes/p/16984572.html