标签：结点 哈夫曼 int 路径 WPL 长度

哈夫曼树

一、定义：

给定N个权值作为N个叶子结点，构建一颗二叉树，使该树的WPL（带权路径长度）最小，即为一颗哈夫曼树（又称最优二叉树）。

二、相关知识：

• 路径和路径长度（L）：

树中的每一个分支即是路径，其中一个结点到根节点的路径总数被称为路径长度。

设根节点的层数为1，则第n层的结点的路径长度为n-1。

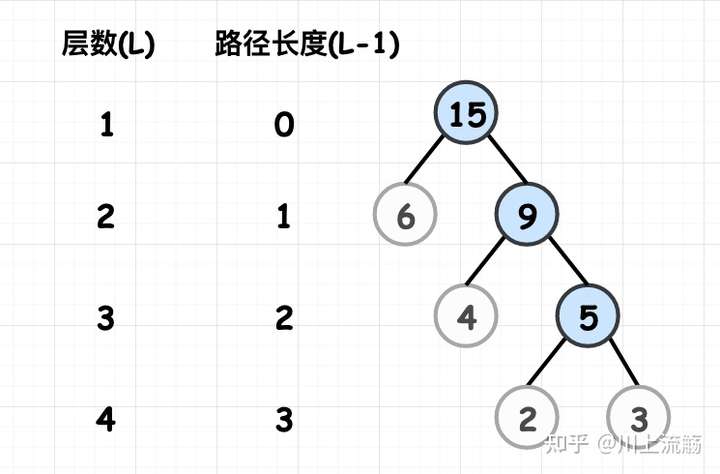
• 带权路径长度（WPL）：

结点的权值乘上其路径长度即为其WPL。

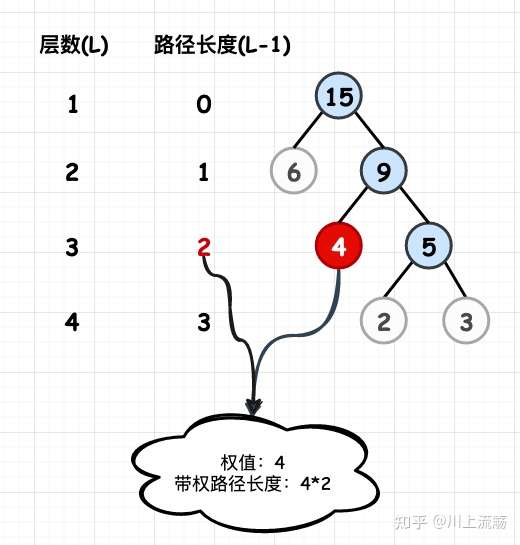
而树的WPL就是树中每个叶子结点的带权路径长度之和。

如上图，树的WPL即为：3*3+2*3+4*2+6*1=29 ;

三、哈夫曼树的构造：

根据定义，我们可以得知，若想让一颗二叉树WPL最小，就需要尽可能地将大权结点往上放，小权结点往下放，以减小其WPL。

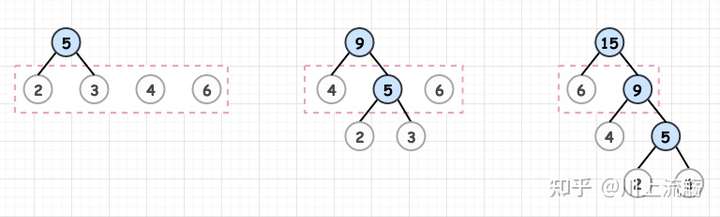
具体过程如下：

1. 先将n个结点看作由n个只有一个根结点构成的树的森林。
2. 按从小到大进行排序，然后选前两个根结点作为新树的子结点，新的根节点权值为子节点权值之和。
3. 从森林中删除选取的两棵树，并将新树加入森林；
4. 重复II、III步，直到只剩下一棵树。

   

四、代码实现：

根据哈夫曼树的性质，可以利用STL中的优先队列实现：

比如：

  给定N个叶子结点的信息，构造一颗哈夫曼树，并输出该树的带权路径长度：

//哈夫曼树
#include <iostream>
#include <queue>
using namespace std;
int n;
priority_queue<int, vector<int>, greater<int>> q; // 大根堆 + 大于号 = 小根堆(因为每次取出的应该是最小值)

int main()
{
    cin >> n;
    while (n -- )
    {
        int x;
        cin >> x;
        q.push(x); // 加入节点
    }
    int ans = 0; // ans: 结果
    while (q.size() > 1) // 模拟哈夫曼树生成过程
    {
        // 挑两个最小的数
        int a = q.top();
        q.pop();
        int b = q.top();
        q.pop();
        
        ans += a + b; // 把他们之和加到答案里
        q.push(a + b); // 合并节点
    }
    cout << ans;
    return 0;
}

 

 

标签：结点,哈夫曼,int,路径,WPL,长度
From： https://www.cnblogs.com/xiaotan-js/p/16633452.html