https://codeforces.com/gym/103470
H. Crystalfly

分析:
可以很好的分析出 一个节点 最多只能选择两个儿子产生贡献
过程就是 u子树中 x y分别为u的儿子并且t[y]=3 u先到x 然后立马折返 回到y
或者直接选择一个点往下走
dp[u][0] 表示在u子树中 并且直接往下走的最大值
dp[u][1] 表示在u子树中 折返后再往下走的最大值
转移
如果是折返再往下走 那么该点的所有儿子都不产生贡献
如果是直接往下走 可能最多有两个儿子产生贡献
具体看代码处理
维护最大次大一定要先跟新次大!!!!! 第二次犯错 这个点位卡了我好久!!!!!
#include<bits/stdc++.h>
using namespace std;
#define lowbit(x) x&(-x)
#define ll long long
const int maxn=1e5+5;
int n;
ll a[maxn],dp[maxn][2];
int t[maxn];
void solve();
vector<int>Q[maxn];
void dfs(int,int);
int main(){
int T;cin>>T;
while(T--)solve();
return 0;
}
void solve(){
cin>>n;
for(int i=1;i<=n;i++)scanf("%lld",&a[i]),Q[i].clear();
for(int i=1;i<=n;i++)scanf("%d",&t[i]);
for(int x,y,i=1;i<n;i++){
scanf("%d%d",&x,&y);
Q[x].push_back(y);
Q[y].push_back(x);
}
dfs(1,1);
cout<<dp[1][0]<<endl;
}
void dfs(int u,int fa){
ll max1=0,max2=0;
ll res=0;
dp[u][0]=dp[u][1]=a[u];
for(int i=0;i<Q[u].size();i++){
int to=Q[u][i];
if(to==fa)continue;
dfs(to,u);
dp[u][1]+=dp[to][0]-a[to];
dp[u][0]+=dp[to][0]-a[to];
if(dp[to][1]-dp[to][0]+a[to]>=max1){
max2=max1;
max1=dp[to][1]-dp[to][0]+a[to];
}else if(dp[to][1]-dp[to][0]+a[to]>max2){
max2=dp[to][1]-dp[to][0]+a[to];
}
}
for(int i=0;i<Q[u].size();i++){
int to=Q[u][i];
if(to==fa)continue;
if(t[to]==3){
if(dp[to][1]-dp[to][0]+a[to]==max1)
res=max(res,a[to]+max2);
else res=max(res,a[to]+max1);
}else res=max(res,a[to]);
}
dp[u][0]+=res;
}
D - Paimon Sorting

分析:
这个题太难了 想了几个小时都没想出来 弄得我想哭
因为要分析每个前缀 所以只有考虑每个数能造成的贡献
先考虑如果每个数都不同的情况
M 表示前i轮的最大值
对于第 i 轮 前i-1个数字一定有序
如果a[i]<M 则第 i个数的贡献就是前i-1个数中大于a[i]的个数
如果a[i]>M 则第 i个数的贡献就是2
为什么?因为如果加上a[i] 之前的M应该变成a[i] 贡献1就是先将M和a[i]换 贡献2 最终M又得回到i位置
现在考虑如果存在相同的数 首先树状数组得去重
如果a[i]=M 也就是连着好几个都等于前i轮的最大 后面第一个比M大的数都会在2的基础上再算一遍
#include<bits/stdc++.h>
using namespace std;
using ll=long long;
const int N=1e5+10;
int tr[N],T,n,vis[N];
void add(int x)
{
for(;x<=n;x+=x&-x) tr[x]++;
}
int query(int x)
{
int res=0;
for(;x;x-=x&-x) res+=tr[x];
return res;
}
int main()
{
cin>>T;
do
{
cin>>n;
ll M=0,ans=0,cnt=0,A=0;
for(int i=1;i<=n;i++)tr[i]=0;
for(int i=1,f=0;i<=n;i++)
{
int x;cin>>x;
if(vis[x]^T)vis[x]=T,add(x);
if(x==M)f=1;cnt+=f;
if(x>M)
{
if(M)ans+=2+max(0ll,cnt-1);
cnt=f=0,M=x;
}
ans+=query(n)-query(x);
cout<<ans<<" \n"[i==n];
}
}while(--T);
}
J. Xingqiu's Joke

题意:
给出两个long long范围内的整数a和b(不相等),每次操作可以对a和b进行以下三个操作之一
a = a + 1, b = b + 1
a = a - 1, b = b - 1
a % d = 0 且 b % d = 0 且 d 是质数, a = a / d, b = b / d
问: 最小需要多少次操作才可将 a 或 b 变为 1
分析:
差值c=b-a 一定是不变的并且 a和b的公共质因数 一定也是c的质因数 设质因数为g
所以可以想到先用前两个步骤 到达上下最近的(g|a,g|b) 考虑记忆化搜索
res=a%g
情况1:可以通过先对a b减去res 到达下最近 此时答案为 res+1+dfs(a/g,b/g)
情况2 :可以通过先对a b加上g-res到达上最近 此时答案为 g-res+1+dfs(a/g+1,b/g+1)
举个例子 11 35 考虑质因数3的时候
11%3=2 达到下最近 2+1+dfs(3,11) 到达上最近 1+1+dfs(4,12)
int c[1001], m;
int ans = inf;
unordered_map<ll, int>mp;
ll h(int a, int b)//哈希函数
{
return a * 1e9 + b;
}
//本题不能单单将a或b当作map的第一维,
//因为可能会出现a相同但b不相同的情况。
//所以可能返回错误的答案,
//因此需要将(a, b)或者(a, b - a)作为哈希map的第一维
int dfs(int a, int b)
{
//记忆化搜索
if (mp[h(a, b)]) return mp[h(a, b)];
//剪枝
if (b - a == 1) return a - 1;
if (a == 1) return 0;
int ans = a - 1;//最差的情况是直接把a减到1
for (int i = 0; i < m; i++)
if ((b - a) % c[i] == 0)//此处要注意判断条件
{
int res = a % c[i];
ans = min({ ans,
res + 1 + dfs(a / c[i], b / c[i]),
c[i] - res + 1 + dfs(a / c[i] + 1, b / c[i] + 1) });
}
return mp[h(a, b)] = ans;
}
int main()
{
IOS;
int T; cin >> T;
while (T--)
{
mp.clear();//可删可不删。本以为不删会速度快,没想到删掉速度快,且memory小了100倍。。可能是hash的数据多了,查找的慢了吧
int a, b; cin >> a >> b;
if (a > b) swap(a, b);
int d = b - a;
m = 0;
for (int i = 2; i <= sqrt(d); i++)
{
if (d % i == 0)
{
c[m++] = i;
while (d % i == 0) d /= i;
}
}
if (d > 1) c[m++] = d;
cout << dfs(a, b) << endl;
}
return 0;
}
I. Cloud Retainer's Game

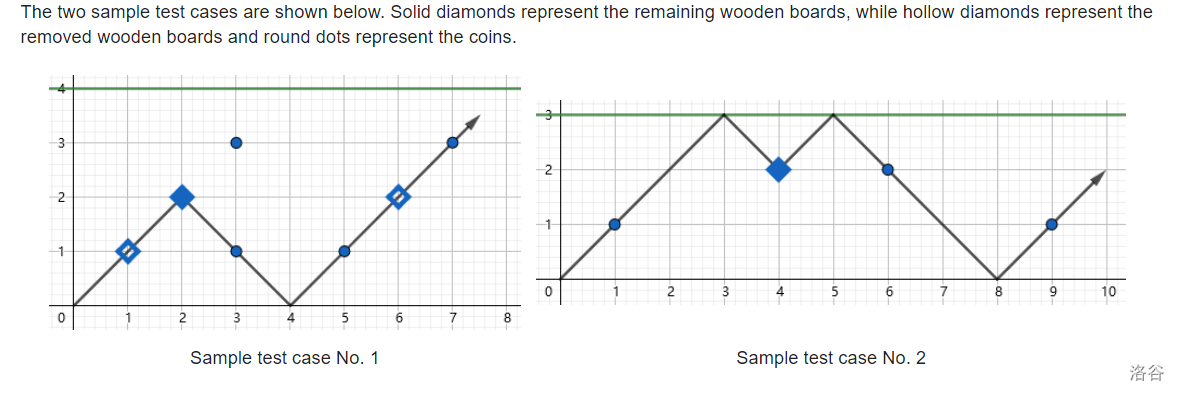
分析:
应该是个线性递推没问题
通过观察可以发现 过(x,y)的两条直线分别为(2*H-y+x) 和 (x+y)
这个(2*H-y+x) 有点难想到
但是对于底边或者上边的位置 直线就会改变 这怎么办?
所以我们需要找到两条成直角的斜线有什么关系
根据图形的特殊性质 来回在两条之间线之间碰撞 想到取模
然后惊奇的发现 如果两条直线在底边或者上边的位置共点 那么取模之后值是相等的
这样问题就迎刃而解了
#include<bits/stdc++.h>
using namespace std;
#define lowbit(x) x&(-x)
#define ll long long
const int maxn=5e5+5;
int n,m,ans,H;
map<int,int>dp;
map<int,int>::iterator id;
struct node{
int x,y,pd;
}a[maxn];
bool cmp(node aa,node bb){
return aa.x<bb.x;
}
void solve();
int main(){
int T;
cin>>T;
while(T--)solve();
return 0;
}
void solve(){
dp.clear();ans=1;dp[0]=1;
scanf("%d%d",&H,&n);
for(int i=1;i<=n;i++)scanf("%d%d",&a[i].x,&a[i].y),a[i].pd=0;
scanf("%d",&m);
for(int i=1;i<=m;i++)scanf("%d%d",&a[i+n].x,&a[i+n].y),a[i+n].pd=1;
sort(a+1,a+1+n+m,cmp);
for(int i=1;i<=n+m;i++){
ll U=(a[i].x+a[i].y)%(2*H),V=(2*H-a[i].y+a[i].x)%(2*H);
if(a[i].pd){
if(dp[U])dp[U]++;
if(dp[V])dp[V]++;
}
else dp[U]=dp[V]=max(dp[U],dp[V]);
}
for(id=dp.begin();id!=dp.end();id++)
ans=max(ans,id->second);
cout<<ans-1<<endl;
}
G. Paimon's Tree



非常好的一道题 但是不会打
标签:return,Contest,int,res,Regional,Asia,long,ans,dp From: https://www.cnblogs.com/wzxbeliever/p/16905749.html