用途(差分)
它可以维护 多次 对序列的一个区间加上一个数,并在最后询问某一位的数或是多次询问某一位的数。(总之修改操作一定要在查询操作之前)
修改的时间复杂度是\(O(1)\),而查询的时间复杂度为\(O(N)\)
一、边差分
将边的差分存在点中(子节点,因为具有唯一性)
需要注意的是,修改的方法和点差分有些许不同
for(int i=1;i<=m;i++){
int a,c;
cin>>a>>c;
int lc=lca(a,c);
b[a]++;
b[c]++;
b[lc]-=2;
//这里b[lc]就要减两次了,因为b[lc]这条边并不在我们期望的路径中,b[f[lc][0]]就更不用管了
}
二、点差分
对于树上的区间(假设为 \([l,r]\)),我们可以把它看成从 \(l\)走到 \(r\)的简单路径
而前缀和就可以看成是每个点的子树和(包括该点)
核心代码
//b数组为差分数组
int b[N];
for(int i=1;i<=k;i++){
int a,c;
cin>>a>>c;
int lc=lca(a,c);//计算出a,c的最近公共祖先,以便处理a,c的简单路径
b[a]++;
b[f[lc][0]]--;//消除a带来的影响
b[c]++;
b[lc]--;//lc这个点实际上会因为a,c加两次,而实际上他只需要加一次,所以减掉一次
}
四、求前缀和
void dfs(int x,int fa){
for(int i=h[x];~i;i=ne[i]){
int j=e[i];
if(j==fa) continue;
dfs(j,x);
b[x]+=b[y];//所有子树的和
}
return ;
}
五、练习题
\(FJ\) 给他的牛棚的 \(N\) 个隔间之间安装了 \(N-1\) 根管道,隔间编号从 \(1\) 到 \(N\)。所有隔间都被管道连通了。
\(FJ\) 有 \(K\) 条运输牛奶的路线,第 \(i\) 条路线从隔间 \(s_i\) 运输到隔间 \(t_i\) 。一条运输路线会给它的两个端点处的隔间以及中间途径的所有隔间带来一个单位的运输压力,你需要计算 压力最大的隔间的压力是多少。
说明/提示
\(2≤N≤5×10^4,1≤K≤10^5\)
题目解析
矩阵的差分应该很简单,典型题目是这样的:
给你一堆数,有\(n\)次修改操作,每次给\(i..j\)这个区间加上\(x\)。最后问所有数中最大的那个。
差分,通俗一点就是把区间的操作改为点操作,在点上记录变化量。上题只需记录\(dlt[i]+=x,dlt[j+1]-=x\),最后用前缀和扫一遍即可。
树上差分,顾名思义就是在树上搞差分。有两种典型题型,一种是边差分,一种是点差分。边差分裸题长这样:

例如有一次操作是把红点(\(u\))到绿点(\(v\))之间的路径全部加\(x\)。那么我就标记\(dlt[u]+=x,dlt[v]+=x\)。
给你一棵树,有\(n\)次修改操作,每次把\(u..v\)的路径权值加\(x\),最后问从\(x..y\)的路径权值和。

这样在最后求解的时候,回溯的时候顺便算一下答案就出来了。
然后我们要在\(lca(u,v)\)处标记\(dlt[lca(u,v)]-=2\times x\)。这样就使得加\(x\)的效果只局限在\(u..v\),不会向\(lca(u,v)\)的爸爸蔓延。
点差分和边差分差别:
有\(n\)次修改操作,每次把\(u..v\)的所有点权都加\(x\),最后问点权最大的为多少,这就是本题问的内容。
做法也是和边差分稍有不同,我们不在\(dlt[lca(u,v)]-=2\times x\),而是把\(dlt[lca(u,v)]-=x\)并把\(dlt[fa[lca(u,v)]]-=x\)。
为什么呢?因为\(lca(u,v)\)也在\(u..v\)这条路径上,它同样需要被加\(x\)。回溯的时候会从\(u\)和\(v\)两个方向都给\(lca(u,v)\)加一个\(x\),而它只能加一个,因此\(dlt[lca(u,v)]-=x\)。而\(lca(u,v)\)的爸爸则根本无法被加,在\(lca(u,v)\)已经只加一个\(x\)了,因此\(dlt[fa[lca(u,v)]]-=x\)就能让\(lca(u,v)\)的爸爸不加\(x\)。
差分 适用于修改多而询问少的情况,本题中只有一次询问,非常适合【别和我说线段树,树链剖分,\(LCT\)云云,赛场上写了\(1\)个小时调了\(1\)个小时结果炸了岂不心态要崩\(orz\)一定是我太菜了调不出来\(orz\)
实现代码
#include <bits/stdc++.h>
using namespace std;
const int N = 3e5 + 10, M = N << 1;
int n, k;
//树上差分模板题【点权】
int depth[N], f[N][25];
int dlt[N];
// 倍增2^k,计算k的办法
// T = log(n) / log(2) + 1;
const int T = 22;
//链式前向星
int e[M], h[N], idx, w[M], ne[M];
void add(int a, int b, int c = 0) {
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}
//倍增求 a,b的最近公共祖先
void bfs(int root) {
queue<int> q;
q.push(root);
depth[root] = 1;
while (q.size()) {
int u = q.front();
q.pop();
for (int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
if (depth[j]) continue;
depth[j] = depth[u] + 1;
f[j][0] = u;
for (int k = 1; k <= T; k++) f[j][k] = f[f[j][k - 1]][k - 1];
q.push(j);
}
}
}
int lca(int a, int b) {
if (depth[a] < depth[b]) swap(a, b);
for (int k = T; k >= 0; k--)
if (depth[f[a][k]] >= depth[b])
a = f[a][k];
if (a == b) return a;
for (int k = T; k >= 0; k--)
if (f[a][k] != f[b][k])
a = f[a][k], b = f[b][k];
return f[a][0];
}
//前缀和
void dfs(int u, int fa) {
for (int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
if (j == fa) continue;
dfs(j, u);
//遍历完j后,dlt[j]已经被填充好,可以合并计算dlt[u]了
dlt[u] += dlt[j];
}
}
int main() {
memset(h, -1, sizeof h);
scanf("%d %d", &n, &k);
for (int i = 1; i < n; i++) { // n-1条边
int a, b;
scanf("%d %d", &a, &b);
add(a, b), add(b, a);
}
//预处理出lca需要的depth数组+f数组(倍增位置数组)
bfs(1);
// k条运输牛奶的路线
for (int i = 1; i <= k; i++) {
int a, b;
scanf("%d %d ", &a, &b);
int lc = lca(a, b);
//点差分
dlt[a]++;
dlt[b]++;
//提前就把1减出去了
dlt[lc]--;
dlt[f[lc][0]]--;
}
//利用前缀和合并差分,此时dlt数组的含义已经不是差分了,而是结果数组了
dfs(1, 0);
int res = 0; //找出结果数组中的最大值即是答案
for (int i = 1; i <= n; i++) res = max(res, dlt[i]);
printf("%d\n", res);
return 0;
}
#include <bits/stdc++.h>
using namespace std;
const int N = 600010, M = N << 1;
int n, m;
int a[N];
//链式前向星
int e[M], h[N], idx, w[M], ne[M];
void add(int a, int b, int c = 0) {
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}
//树上差分模板题【点权】
int depth[N], f[N][31];
int dlt[N]; //差分数组
// 倍增2^k,计算k的办法
// T = log(n) / log(2) + 1;
const int T = 25;
//倍增求 a,b的最近公共祖先
void bfs(int root) {
queue<int> q;
q.push(root);
depth[root] = 1;
while (q.size()) {
int u = q.front();
q.pop();
for (int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
if (depth[j]) continue;
depth[j] = depth[u] + 1;
f[j][0] = u;
for (int k = 1; k <= T; k++) f[j][k] = f[f[j][k - 1]][k - 1];
q.push(j);
}
}
}
int lca(int a, int b) {
if (depth[a] < depth[b]) swap(a, b);
for (int k = T; k >= 0; k--)
if (depth[f[a][k]] >= depth[b])
a = f[a][k];
if (a == b) return a;
for (int k = T; k >= 0; k--)
if (f[a][k] != f[b][k])
a = f[a][k], b = f[b][k];
return f[a][0];
}
//前缀和
void dfs(int u, int fa) {
for (int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
if (j == fa) continue;
dfs(j, u);
dlt[u] += dlt[j];
}
}
int main() {
memset(h, -1, sizeof h);
scanf("%d", &n);
for (int i = 1; i <= n; i++) scanf("%d", &a[i]); //需要按a[i]规定的路线逐个走
//表示标号 a 和 b 的两个房间之间有树枝相连
for (int i = 1; i < n; i++) {
int a, b;
scanf("%d %d", &a, &b);
add(a, b), add(b, a);
}
//预处理出lca的depth数组和f倍增数组
bfs(1);
// lca查表+树上点权差分
for (int i = 1; i < n; i++) { // n-1条边
int x = a[i], y = a[i + 1];
int lc = lca(x, y);
//点权
dlt[x]++;
dlt[y]++;
dlt[lc]--;
dlt[f[lc][0]]--;
}
//将差分还原回原始数组
dfs(1, 0);
//我们仔细想想可以发现,每一个路径的终点又是下条路径的起点,而我们对其修改了两遍,所以这个算法就有问题了
//对每条路径修改后,将终点的值减1:这样的话,就不存在重复覆盖的问题了,而且这也恰好符合了终点要 -1的情况
for (int i = 2; i <= n; i++) dlt[a[i]]--;
//输出每个房间需要放的糖果数量
for (int i = 1; i <= n; i++) printf("%d\n", dlt[i]);
return 0;
}
\(HDU5452\) \(Minimum\) \(Cut\)
题目大意:
给你\(n\)个点,\(m\)条边。规定前\(n-1\)条边为生成树。要求从这个生成树中删掉一条边,让这个图不连通,问加上树上这条边,最少 删几条边。
解题思路
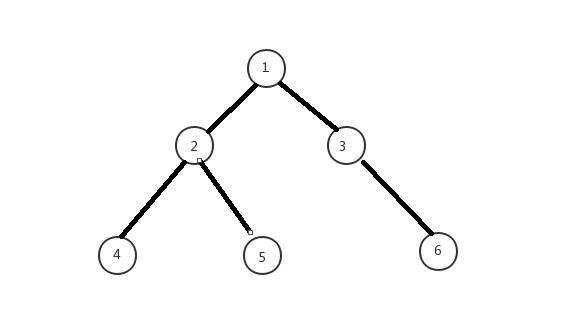
如图,这是一棵树,如果存在一条边(\(3,5\))(图中的虚边)
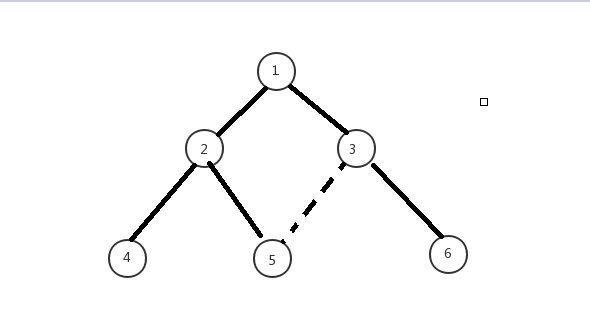
如果你想删树上的(\(2,5\))这条边让图不连通,那么你就必须删掉(\(3,5\)),只有\((2,5) (3,5)\) 同时被删,才能够让图不连通。同样,如果你想删除\((1,2)\)这条边,那么你也必须删除\((3,5)\)这条边。所以\((3,5)\)这条虚边,会对\(3——5\)路径上所有的点贡献\(1\)。
同样,如果有一条虚边\((2,6)\),那么会对\(2-6\)路径上的\((2,1) (1,3) (3,6)\)三条边都贡献\(1\).
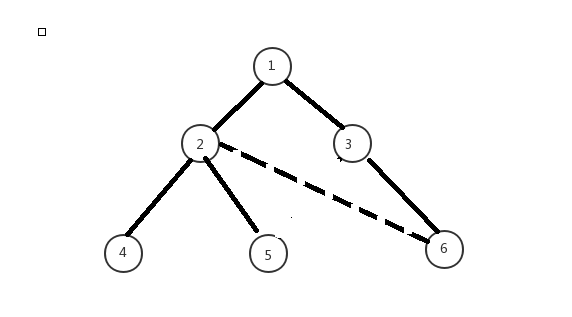
那么问题就转边成了:
有一个边集(除了前\(n-1\)条边,剩下的边),边集里的边对树上的边有贡献,边集里的每条边(\(u,v\))对树的路径\(u—v\)上的所有边的贡献都是\(1\)。最后求树上权值最小的边,让这个权值加\(1\)就是答案(\(+1\)是因为还要删掉它自己)。
那么如何求呢?就是用 树上差分 了。
#include <bits/stdc++.h>
using namespace std;
const int INF = 0x3f3f3f3f;
const int N = 2e4 + 10, M = 2e5 + 10;
//链式前向星
int e[M], h[N], idx, w[M], ne[M];
void add(int a, int b, int c = 0) {
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}
int depth[N], f[N][31];
int dlt[N]; //差分数组
// 倍增2^k,计算k的办法
// T = log(n) / log(2) + 1;
const int T = 25;
//倍增求 a,b的最近公共祖先
void bfs(int root) {
queue<int> q;
q.push(root);
depth[root] = 1;
while (q.size()) {
int u = q.front();
q.pop();
for (int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
if (depth[j]) continue;
depth[j] = depth[u] + 1;
f[j][0] = u;
for (int k = 1; k <= T; k++) f[j][k] = f[f[j][k - 1]][k - 1];
q.push(j);
}
}
}
int lca(int a, int b) {
if (depth[a] < depth[b]) swap(a, b);
for (int k = T; k >= 0; k--)
if (depth[f[a][k]] >= depth[b])
a = f[a][k];
if (a == b) return a;
for (int k = T; k >= 0; k--)
if (f[a][k] != f[b][k])
a = f[a][k], b = f[b][k];
return f[a][0];
}
//前缀和
void dfs(int u, int fa) {
for (int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
if (j == fa) continue;
dfs(j, u);
dlt[u] += dlt[j];
}
}
int main() {
int T, n, m;
scanf("%d", &T);
int cc = 0;
while (T--) {
idx = 0;
memset(h, -1, sizeof h);
memset(depth, 0, sizeof depth);
memset(dlt, 0, sizeof dlt);
scanf("%d%d", &n, &m);
for (int i = 1; i < n; i++) {
int a, b;
scanf("%d%d", &a, &b);
add(a, b), add(b, a);
}
bfs(1);
for (int i = n; i <= m; i++) {
int a, b;
scanf("%d%d", &a, &b);
//树上差分+边权(把边权记在点上)
dlt[a]++;
dlt[b]++;
dlt[lca(a, b)] -= 2;
}
//前缀和合并差分
dfs(1, 0);
int res = INF;
for (int i = 2; i <= n; i++)
if (dlt[i] == 0)
res = 1;
else
res = min(res, dlt[i] + 1);
printf("Case #%d: %d\n", ++cc, res);
}
}