[论文阅读] 颜色迁移-EM概率分割的局部颜色迁移

颜色迁移-EM概率分割的局部颜色迁移

文章: Local Color Transfer via Probabilistic Segmentation by Expectation-Maximization,[paper][code(未公开)]

本文目的为: 图像局部颜色迁移.

1-符号说明

在进行本文算法原理说明之前, 先对一些英文缩写进行简单说明:

1. EM: Expectation-Maximization, 期望最大化, 是一种非监督期望最大化算法, 结合了极大似然和迭代求解的方法去预估数据的分布, 详见: 期望最大化（Expectation Maximization）算法介绍_Y学习使我快乐V的博客-CSDN博客_expectation maximization, EM（Expectation-Maximization）算法（通俗易懂） - 知乎 (zhihu.com), 最大期望算法(Expectation-Maximization algorithm，EM) - 八九十度 - 博客园 (cnblogs.com)
2. GMM: Gaussian Mixture Model, 高斯混合模型, 混合高斯模型, 使用多个高斯分布来拟合数据分布, 详见: 一文详解高斯混合模型原理 - 知乎 (zhihu.com), 详解EM算法与混合高斯模型(Gaussian mixture model, GMM)_林立民爱洗澡的博客-CSDN博客_gmm

2-算法原理

简单来说, 本文对图像进行颜色分割, 对分割后区域单独进行颜色迁移, 对各区域迁移后的图像进行加权平均得到最后图像, 具体:

1. 使用调整后的EM算法进行颜色分割
2. 寻找每个区域的映射关系
3. 对每个区域单独进行颜色迁移
4. 将迁移后的图像进行加权平均得到最后的迁移图像

3-算法核心

为了利用局部信息, 本文利用GMM来描述图像颜色分布, 并使用EM进行概率分割, 因而EM算法对图像进行颜色分割是关键. 本文对EM进行了调整, 主要有2个方面: 一是期望计算, 二是对概率滤波.

3.1-E-step

E-step是计算每个像素属于每个区域的概率(将图像分为N区域), 原始计算期望及均值方差的方法如下,

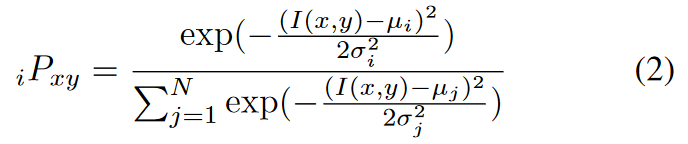
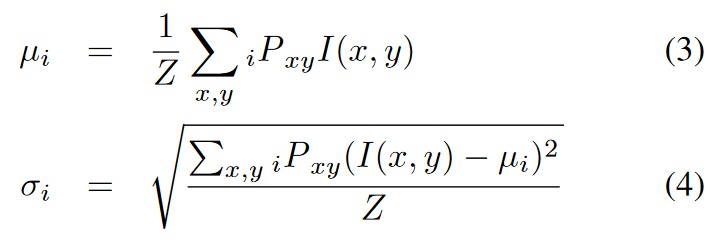
与原始计算方式不一样, 更改后的计算方式为: 使用前一次滤波后的结果与当前结果进行加权, 如下所示:

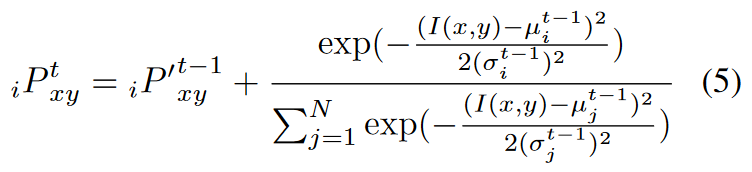
文中对于这样做的解释是:

• 如果前一次滤波后的结果与当前结果具有相似的分布, 则相邻像素极有可能具有相似的颜色值, 这表明该像素不位于任何区域边界上, 因此, 加法操作增加了像素属于某些占主导地位的高斯分量的概率
• 如果具有不同的概率分布, 则像素可能处于区域的边界处, 加法运算使这些分布平均, 因此这个像素将有相似的概率同时适合几个高斯分量

3.2-概率滤波

本文在进行GMM分割时, 仅考虑了颜色信息, 没有使用空位位置信息. 对于相邻像素, 如果它们有相似的颜色, 他们的高斯分布也应该相似, 即概率也是要相似的.

因而为了增加空间相关信息, 使用了空间滤波方法对概率进行滤波处理. 本文使用的是调整后的双边滤波, 如下所示:

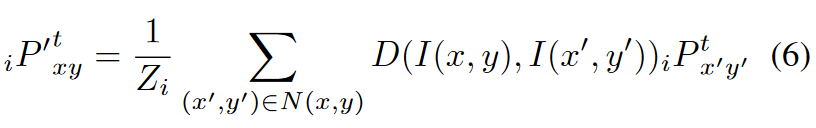
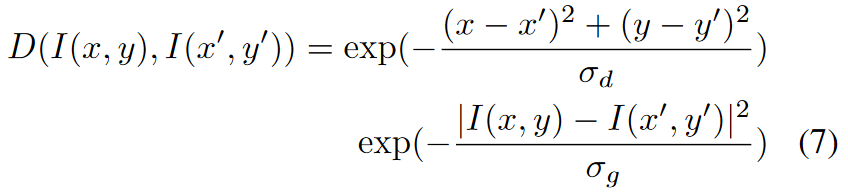
可以看到, 文中使用的滤波方式是: 在图像上计算双边滤波权重, 然后对概率进行加权平均. 作者没有解释为什么这样做, 为什么不直接在概率上计算权重.

我的理解是:

• 计算出来的期望图(每个像素属于每个区域的概率)是一个软的边界, 图像中的细节边缘可能已经没有那么明显了, 如果直接对概率进行滤波, 就不能很好的保护边缘信息
• 一般图像中的区域会>>图像的颜色通道数, 这样期望图的通道数也会>>图像的颜色通道数, 这样对期望图(概率)进行滤波会比图像进行滤波难
• 还有一点, 我认为比较重要的是: 期望图是迭代生成的, 每次迭代都需要重新计算, 而对原始图像进行滤波处理, 只需要计算一次即可, 可以节省算法耗时

滤波对结果的影响还是很大的, 滤波窗口不能太大也不能太小, 文中做实验进行了验证, 如下所示, 最后设置为7.

图中N为滤波窗口大小, 如果超过目标大小, 目标没有被检测出来, 最后颜色迁移不成功; 如果串口大小小于目标大小, 对目标边缘有影响, 颜色迁移后图像边缘颜色存在异常.

4-算法效果

如下所示为文中给出的一组结果:

图(b)-(d)为概率分割结果, (e)为直方图均衡结果, (f)为全局颜色迁移结果, (g)为本文局部迁移结果

下图为另一组结果:

图( c)为本文结果, (d)为全局颜色迁移结果, (e)为直方图均衡结果

5-补充说明

关于本文算法, 还有一些需要补充的说明:

1. 本文算法是在Lab颜色空间进行处理的
2. 在进行GMM-EM概率分割时, 使用Kmeans进行的初始化, 这个就对初始点的设置有一定的要求, 如果使用随机初始化, 可能每次结果还不一致
3. 分割过程中, 会对比较接近的高斯模型(均值距离<阈值)进行合并, 并重新计算参数, 但没有详细说明这个阈值参数的设置
4. 分割成颜色块之后, 颜色块之间的对应关系没有详细说明, 仅说明了2个规则, 对于图像分割后的颜色块数量不一致时(如合并完成后, target图像的颜色块>>source图像的颜色块), 如何处理映射关系文章中也没有介绍
   - 亮度空间(L通道)最接近
   - 保持单调性
5. 文中对每个颜色块计算映射, 最后对所有映射迁移后的图像使用概率图进行加权平均融合

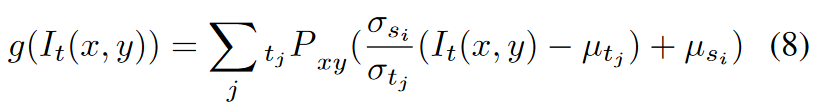
6. 文中使用的算法, Kmeans, GMM-EM, bilateral filter都是比较耗时, 因而处理比较大的图像时是非常耗时, 文中也给出自己的耗时测试: Pentium-M 1.4GHz laptop computer, 512*512, 20 Gaussians initially, 耗时4分钟!!! 这结果...

另外本文使用的都是很成熟的算法, 没有太大的改动, 方便实现, 但有些地方感觉没有写清楚(可能是没有看懂, 特别是颜色块处理), 同时也没有给出测试图像, 因而也不方便复现. 下面是使用matlab自带的kmeans和GMM相关函数实现的分割, 后面的颜色迁移没有进行复现.

原始图像是使用搜图, 找到的比较类似的图像. 原始图像地址

原图

Kmeans结果

GMM结果

最后, 关于GMM的matlab实现, 可以参考: MATLAB中“fitgmdist”的用法及其GMM聚类算法 - 凯鲁嘎吉 - 博客园 (cnblogs.com)