2022/11/12 模拟测题解

2022/11/12 模拟测题解

A

考场上推了一下，发现这个玩意挺有意思。一共有 \((n+1)(m+1)\) 个字符串，减去相同的个数，即可。

这个相同的个数还是很好统计的，且这里指的相同仅仅是 挪动一位 的相同，具体可以参考下图。

所以我们只需要统计 中间这两个相同 的个数即可。代码在学校，没有。

B

首先，显然的，我们每条 \((u,v)\) 边的边权只可能是 \(m,a_u,a_v\) 其中一个。

我们不妨分两种情况来考虑：边权大于 \(\min(a_u,a_v)\) 的情况和小于等于的情况。

我们发现，\(u\) 的每个子树 \(v\) 如何分配边权，显然与 \(u\) 无关，仅与 \(u\to v\) 这一条边的边权与有关，如下图。

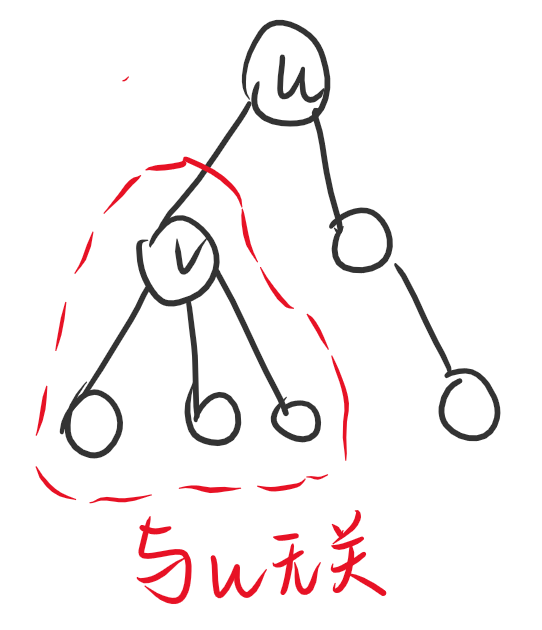
于是，我们可以考虑在树上进行 DP。设 \(f_{i,0/1}\) 为考虑 \(i\) 节点及其子树，\(i\) 的父节点到 \(i\) 的这条边的边权大于/小于等于 \(\min(u,v)\) 所能得到的最大收益。

那么就可以转移了。注意，不能一味的认为大于 \(\min(u,v)\) 就是等于 \(m\)。实际上，\(\min(u,v)\) 有可能大于 \(m\)。

如何转移：由于是中位数，所以你显然要有 \(size_u\div 2\) 条边是 \(\min(u,v)\)，所以你贪心选取即可。

C/D

待会补。