想了两种做法,第一种拿到了 10 分的好成绩。
而第二种做法不用前缀和,而且还跑的飞快。目前最优解第三尝试卡进最优解未果。
不得不说这是一道好题,做完对 KMP 有了更深的理解。
1.(本人的) KMP 究竟哪里错了
首先,看到匹配,第一眼想到 KMP。接着就能发现实际上分隔符 * 实际上就是把一整个字符串分成了若干个小串,匹配完一个才能匹配下一个。
然后有一个显而易见的结论:每一个小串能完全匹配时就要匹配,因为之后的 * 可以匹配任意长的字符串(但要注意匹配最后一个小串终点的特判)。
于是我们可以口胡出一个看起来很对的做法:对每个小串做 KMP,遇到问号直接当做匹配,然后在询问串上跑匹配完一个小串就进入下一个小串。时间复杂度线性。
正如前言所说,你可以在我的提交记录看到夺目的 10 分。为什么错了呢?
考虑这样一个串:aca?c 。按照 KMP 数组的定义,求出的失配指针应该为 \(0,0,1,2,2\)。但实际上,如果我们按照上述步骤来求,答案会是这样:\(0,0,1,2,0\)。
为什么呢?设字符串为 \(s\),当前自匹配到 \(j\),失配数组为 \(fail\),那么当我们循环到最后一个字符时,我们要将 \(s_{j+1}\) 也就是 \(s_3\) 与 \(s_5\) 比较。发现不行,这时我们的 \(j\) 会回跳到 \(fail_j\) 也就是 \(s_0\) 处。这似乎是一个正常的 KMP 过程。
但是 KMP 的优化在此时会默认本来为 ? 的 \(s_4\) 为 a 。因为计算机会认为既然 \(s_2\) 与 \(s_4\) 相匹配,那么 \(s_4 = s_2\) 也是理所因当的。这时失配指针往回跳时就没有考虑 \(s_4\) 发生变化的情况,它只会憨憨地认为 ac 与 cc 不匹配,所以应该跳回起点。
至此,我们的问号直接跳计划宣告破产。
2.跑的飞快的哈希做法
一个串与一个串匹配,除了 KMP ,我们还可以想到哈希。在以 * 为分隔将大串分割为小串后,每一个小串的长度固定。于是可以直接扫询问的字符串,每次提取出当前小串长度的字符串 \(O(1)\) 求哈希值。
说具体点,你首先从起点提取出小串长度的字符串,顺便记录一下最左边乘了几次哈希的单位,然后转移时删除最左边的权值乘最左边乘过的哈希单位就行。
下面是一张图,假设小串长度为 3:
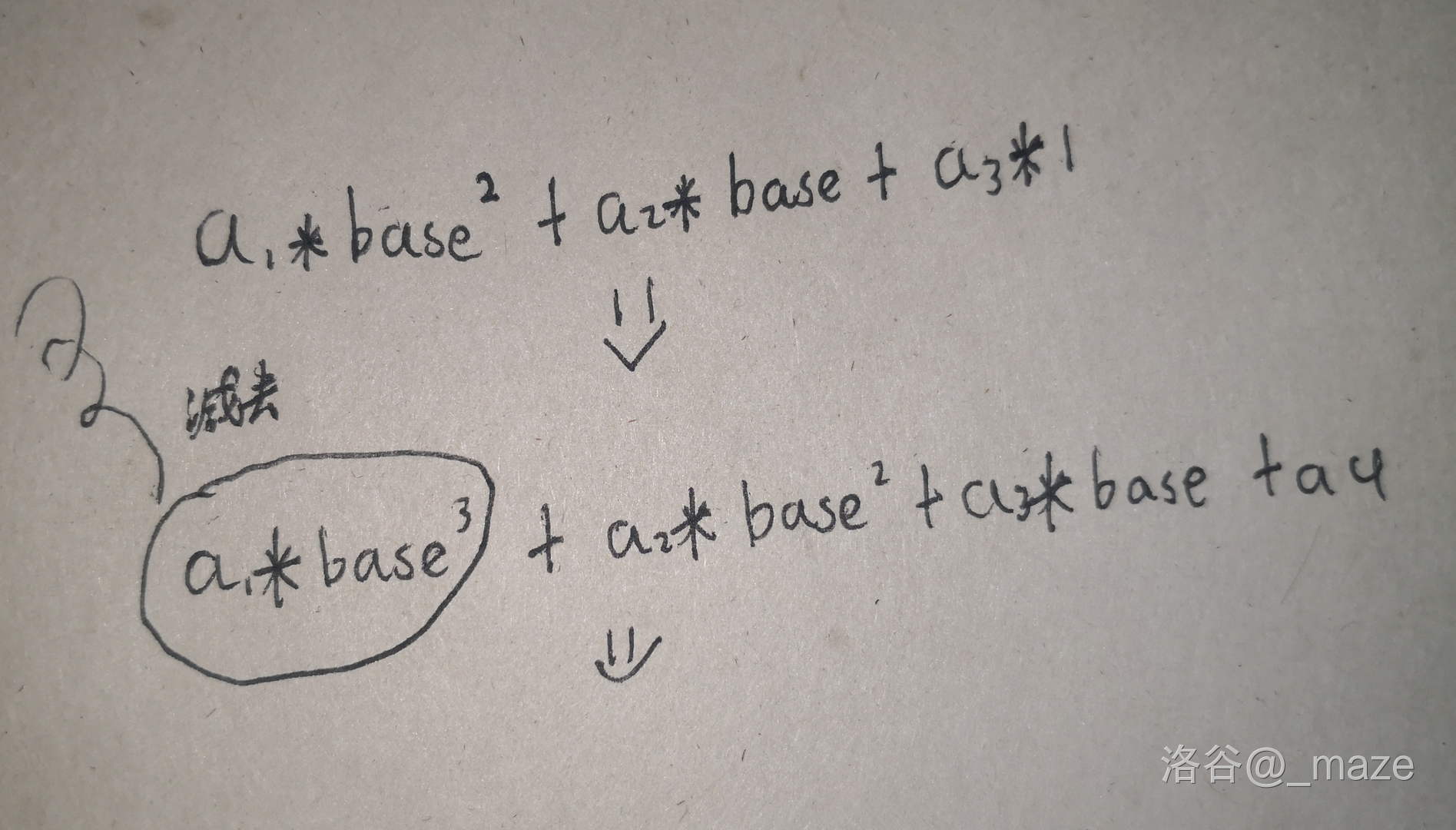
不许说我字丑!
那问号怎么办呢?我们把问号的权值置为 0,动态记录当前询问串中哪几个串与问号对应,将这些点的权值强制赋为 0(方法可参照减去最左端权值的方法),向后推进时暴力转移,将所有与问号对应的下标加一即可。
由于问号最多只有 10 个,所以复杂度就是 \(O(n)\) 带了个 10 的常数。
这一道题还有一些小细节需要注意:
- 开头除非有一个
*挡着,否则第一个小串一定要与询问串前缀匹配。所以要特判,否则会在第三个点 WA。 - 到最后除非有一个
*挡着,否则最后一个串一定要与询问串后缀匹配。如果最后一个串匹配了却不是与后缀匹配的,那么就不能结束,还要继续比较。 - 每一次向后推进时,先加上原先串被强制赋为 0 的点的权值,再减去最左边的权值乘上它的幂,(详情参照上图)并加上下一位权值,最后再将当前与问号匹配的点强制赋为 0。如果第一二步顺序乱掉的话会导致被开头是
?的数据 hack 掉。因为此时最左边的权值减了两遍。
#include <bits/stdc++.h>
#define ull unsigned long long
using namespace std;
#define rep(i,a,b) for(int i =(a);i <= (b);i ++)
const int maxn = 1e5 + 5;
const ull base = 19260817;
int len[maxn], tot;
bool pd[15];
string s, p[maxn];
ull H[maxn];
bool hjl, hzh;
ull qpow(ull u, ull v)
{
ull ans = 1;
while(v)
{
if(v & 1) ans *= u;
u *= u;
v >>= 1;
}
return ans;
}
void solve()
{
int n = s.size();
s = ' ' + s;
ull ha = 0, now = 1;
bool pd = 0;
ull en[12], st = -1, cnt = 0, mi[12], big = 0;//st为最左边的下标,en与cnt存储与问号匹配的点,mi统计与问号对应的点乘了几次base,big统计最左端乘了几次base
rep(i, 1, n)
{
int li = i;
if(pd == 0)
{
st = i;
int m = p[now].size() - 1;
cnt = 0;big = 1;ha = 0;
rep(j, 0, m)
{
ha *= base;
if(j > 0) big *= base;
if(p[now][j] != '?')
{
ha += (ull)(s[i] - 'a' + 1);
}
else
{
en[++ cnt] = i;//顺便记录每个?的初始对应位置
mi[cnt] = qpow(base, m - j);
}
i ++;
}
pd = 1;
if(ha == H[now]) //一开始提取出的串也要进行匹配
{
int o = 0;
if(now < tot) now ++, pd = 0, o = 1;
if(o == 0 && (i >= n || hzh == 1))//即使所有串匹配完了也不一定完全匹配,具体参照上文提醒
{
cout << "YES" << endl;
return;
}
}
else if(hjl == 0 && li == 1)
{
cout << "NO" << endl;
return ;
}
i --;
continue;
}
rep(j, 1, cnt) ha += (ull)(s[en[j]] - 'a' + 1) * mi[j], en[j] ++;
ha -= (ull)(s[st] - 'a' + 1) * big;
ha *= base;
ha += (ull)(s[i] - 'a' + 1);
st ++;
rep(j, 1, cnt) ha -= (ull)(s[en[j]] - 'a' + 1) * mi[j];//注意顺序
if(ha == H[now])
{
int o = 0;
if(now < tot) now ++, pd = 0, o = 1;
if(o == 0 && (i >= n || hzh == 1))
{
cout << "YES" << endl;
return;
}
}
}
cout << "NO" << endl;
return ;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin >> s;
int n = s.size();
string c = "";
rep(i, 0, n - 1)
{
if(s[i] == '*')
{
if(i == 0) hjl = 1;
if(i == n - 1) hzh = 1;//如果开头结尾有*,那么没有匹配前后缀的字符串也能视作完全匹配
if(c != "") p[++ tot] = c, c = "";
}
else c = c + s[i];
}
if(c != "") p[++ tot] = c;
rep(i, 1, tot)
{
int m = p[i].size();
rep(j, 0, m - 1)
{
H[i] *= base;
if(p[i][j] != '?') H[i] += (ull)(p[i][j] - 'a' + 1);
}
}
int Q;
cin >> Q;
while(Q --)
{
cin >> s;
solve();
}
}
本篇题解就到这里了,考虑考虑点个推荐,然后去把本菜鸡从最优榜上挤下去?
标签:匹配,P3167,题解,KMP,int,权值,CQOI2014,小串,问号 From: https://www.cnblogs.com/closureshop/p/16882153.html